Как с помощью линейки нарисовать шестиугольник: Как нарисовать шестиугольник с помощью линейки
Как нарисовать шестиугольник с помощью линейки
Пятиугольник
Здравствуйте коллеги.Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.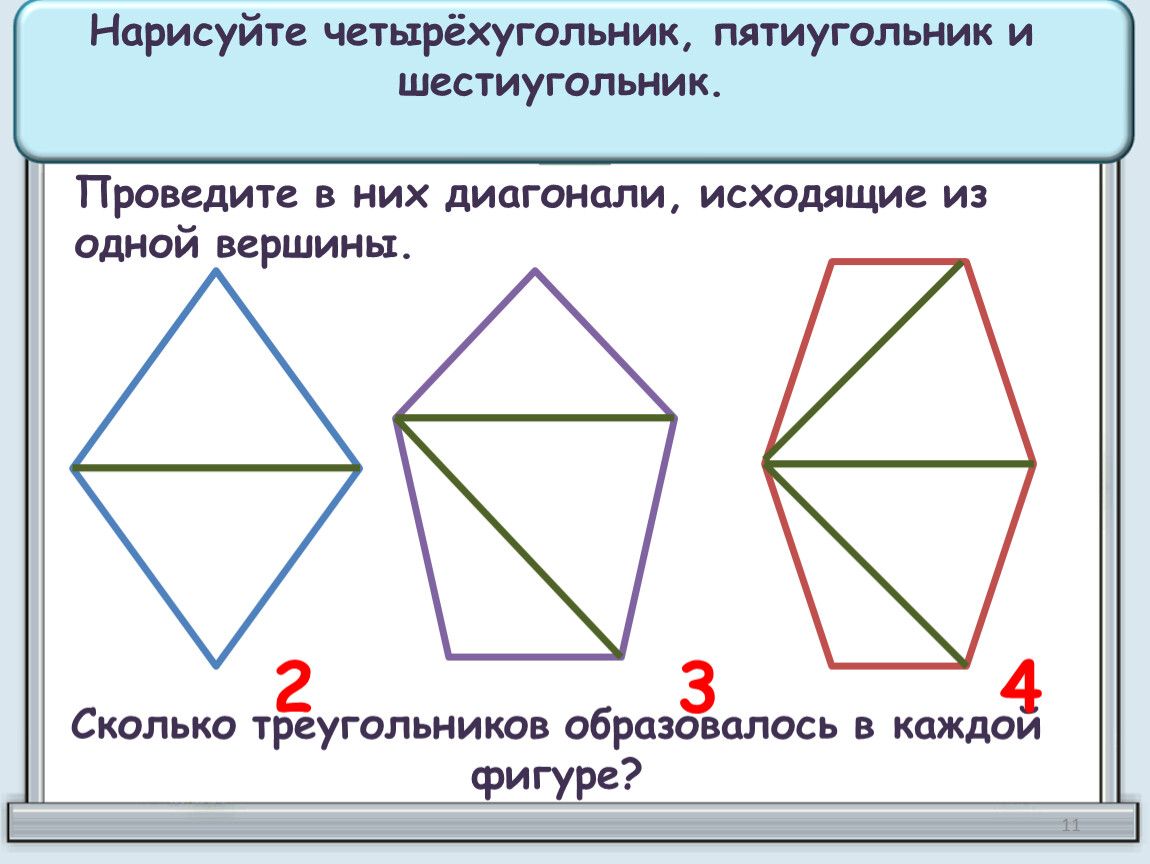
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Как построить и нарисовать правильный пятиугольник по окружности
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов.
 Сумма всех внутренних углов: 108*5 = 540 градусов.
Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.

- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Я РАСТУСайт для детей и их родителейПоследние события
Как из картинки сделать раскраску?
Раскраски любят и дети, и взрослые. И это неудивительно. Ведь даже не умея профессионально рисовать, можно создавать красивые рисунки, вкладывая в них своё умение и виденье .
Рисуем цыпленка
Вот такого цыпленка вы сможете нарисовать, если вы выполните все действия четко по шагам. Пробуйте и все у вас получится!
Елка-раскраска на стену
А так как скоро Новый Год, предлагаю скачать шаблон большой елки-раскраски. Этот шаблон состоит из 22 двух листов формата А4. На них нанесен и основной рисунок, и линии по которым нужно эти листочки склеить.
Дедушка Мороз и дети
Дед Мороз, Снегурочка, Снеговик, птицы и звери в лесу , дети на новогоднем празднике — вот герои этой книжки-раскраски. А создал их художник В. Жигарев.Маша и Медведь. Зимние раскраски
Мультик про шуструю озорную маленькую девочку Машу и ее приятеля медведя нравится всем — и детишкам, и их родителям.Раскраски с дедом Морозом
Новый год наступил. Но впереди еще старый новый год, да и зима еще вся впереди. Раскрашиваем картинки с Дедом Морозом и Снегурочкой.Раскраски к новому году
Новогодние раскраски. Зима, елка, дед Мороз в санях, подарки. Скачайте забавные картинки, пусть они напоминают вам о веселом празднике.
Популярное
Архив
Как нарисовать правильную звездочку
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Построение на плоскости
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
1. Построим угол в 60, как описано выше, и разделим его пополам.2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .
Построение правильного шестиугольника.
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G .
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .
Общий метод построения многоугольников.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Линейно-конструктивный рисунок шестигранной призмы
Научимся изображать шестигранную призму в различных положениях.
Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыГоризонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис.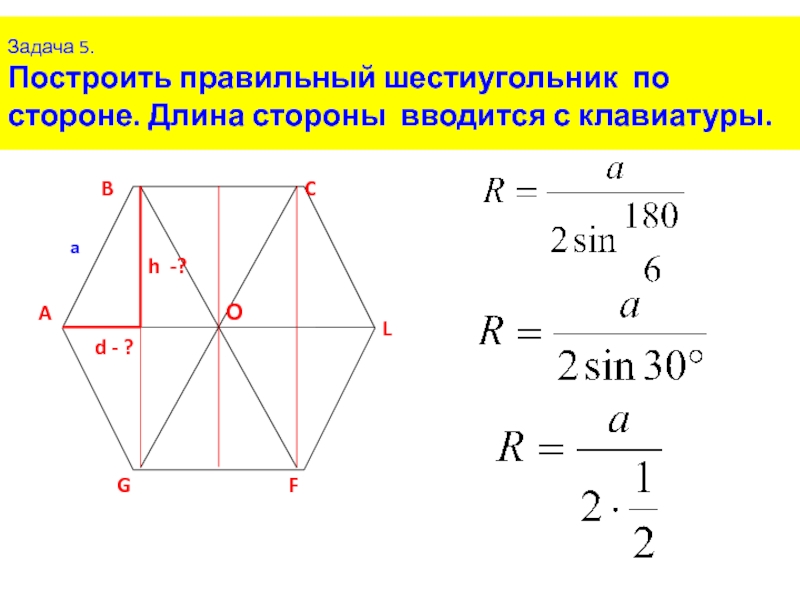 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыКроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Как нарисовать невозможный шестиугольник – Невозможные фигуры
Понравились мои уроки рисования? Получите больше на YouTube:
Нажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Что такое невозможный объект? Также называемые невозможными фигурами или неразрешимыми фигурами, эти рисунки являются разновидностью оптического обмана. Двумерная фигура кажется трехмерной, но геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные предметы использовались в интригующих произведениях искусства на протяжении всего двадцатого века.
Невозможный шестиугольник в этом руководстве по рисованию основан на треугольнике Пенроуза, который был создан художником в 1934 году. Полигоны Пенроуза, такие как этот шестиугольник, строятся путем добавления дополнительных сторон к треугольнику Пенроуза.
Тем не менее, оптическая иллюзия становится менее яркой, поскольку добавляется больше сторон. Таким образом, шестиугольник может казаться искривленным, заплетенным или искривленным, а не «невозможным».
Шестиугольники являются общими структурами как в искусстве, так и в природе. Вы знали? Соты сделаны из маленьких шестиугольников пчелиного воска. Интересно, что шестиугольник позволяет покрывать большое пространство как можно меньшим количеством воска.
Хотите нарисовать невозможный шестиугольник? Сделать это легко и весело с помощью этого простого, пошагового руководства по рисованию фигур. Все, что вам нужно, это карандаш, ручка или маркер и лист бумаги. Вы также можете покрасить свой законченный рисунок.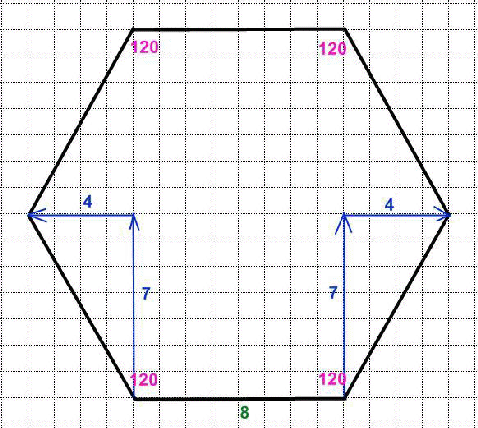
Пошаговая инструкция по рисованию – Невозможный шестиугольник
1. Начните с рисования шестиугольника. Шестиугольник — это правильная шестигранная фигура, в которой все стороны имеют одинаковую длину.
2. Нарисуйте короткую линию, идущую от верхнего угла шестиугольника. От этой линии вытяните более длинную линию, параллельную стороне шестиугольника. Затем от конца этой линии протяните прямую линию, параллельную следующей стороне шестиугольника. Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
3. Нарисуйте короткую прямую линию, идущую от следующего угла шестиугольника. Протяните от него прямую линию, параллельную стороне шестиугольника.
4. Протяните короткую прямую линию от нижнего угла шестиугольника. Из этой линии нарисуйте прямую линию, параллельную нижней части шестиугольника. Затем продлите еще одну линию вверх, параллельно следующей стороне шестиугольника.
5. Проведите короткую линию от оставшегося нижнего угла шестиугольника. Отсюда нарисуйте прямую линию, параллельную стороне шестиугольника. Затем проведите еще одну линию параллельно следующей стороне шестиугольника.
6. Нарисуйте короткую прямую линию, выходящую из следующего угла шестиугольника. Затем протяните прямую линию, параллельную стороне шестиугольника.
7. Проведите короткую прямую линию от последнего угла шестиугольника. Отсюда вытяните прямую линию, параллельную вершине шестиугольника.
8. Начните соединять внешние края невозможного шестиугольника. Расширьте короткие линии от верхнего угла и стороны формы. Затем соедините эти линии с существующими линиями, заключив верхнюю и верхнюю часть рисунка.
9. Проведите короткую линию, идущую от нижнего угла шестиугольника. Затем соедините все открытые линии, пока фигура не будет полностью заключена.
Цвет и тень вашего невозможного шестиугольника. Обратите внимание, как затенение в нашем примере делает трехмерную иллюзию более яркой.
Урок 26. построение правильных многоугольников — Геометрия — 9 класс
Для построения правильных n-угольников при n>4 обычно используется окружность, описанная около многоугольника.
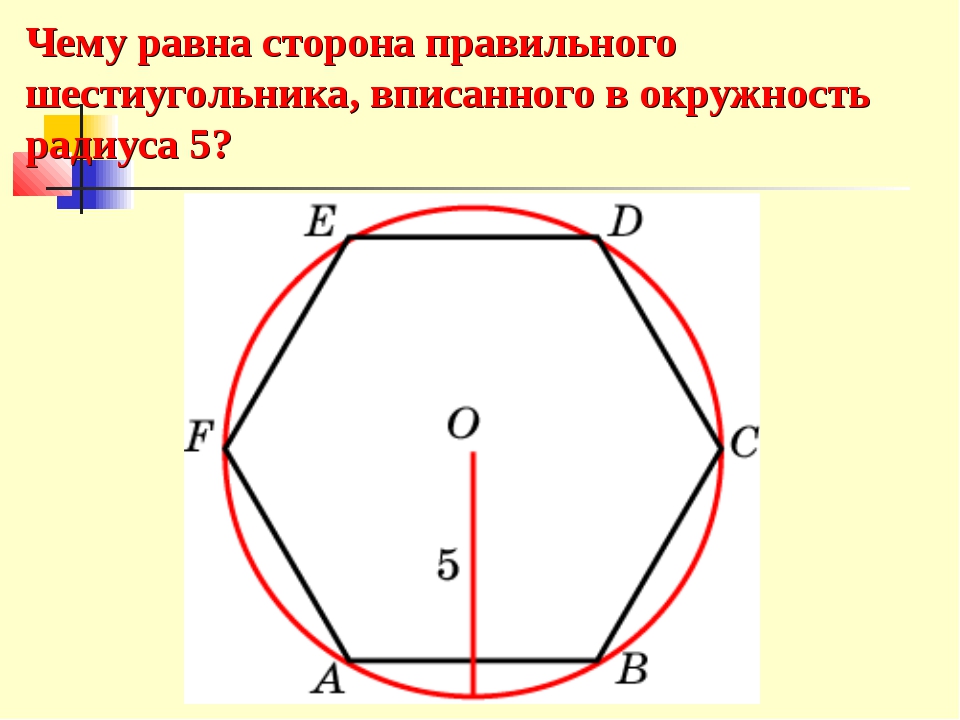
Задача 1. Построим правильный шестиугольник, сторона которого равна данному отрезку
Воспользуемся формулой для стороны правильного шестиугольника:
a6 = 2Rsin (180°)/6 = 2R sin30° = 2R ∙ 1/2 = R, т.е. сторона шестиугольника равна радиусу описанной окружности.
Построим с помощью отрезка PQ окружность, радиусом которой будет являться данный отрезок.
Отметим на окружности точку А1 в произвольном месте. Для построения остальных точек возьмем циркуль. Зафиксируем его раствор размером с выбранный нами отрезок. Не меняя раствора циркуля, построим на окружности точки А2, А3, А4, А5, А6, таким образом, чтобы выполнялись равенства отрезков
Соединим точки отрезками. Получим искомый правильный шестиугольник
Задача 2. Дан правильный n-угольник. Построить правильный 2n-угольник.
Пусть А1А2А3Аn правильный n-угольник. Начертим описанную окружность. Для этого построим биссектрисы углов А1 и А2. Точку пересечения биссектрис, а это центр окружности, обозначим буквой О. Из точки пересечения биссектрис проведем окружность радиуса
 Точки деления дуг обозначим как В1, В2 и так до Вn. Для построения точек В1, В2 до Вn можно воспользоваться серединными перпендикулярами к сторонам рассматриваемого нами многоугольника.
Точки деления дуг обозначим как В1, В2 и так до Вn. Для построения точек В1, В2 до Вn можно воспользоваться серединными перпендикулярами к сторонам рассматриваемого нами многоугольника.Соединим эти точки с концами соответствующей дуги, т.е. с вершинами многоугольника.
Таким образом, построен правильный двенадцатиугольник из шестиугольника.
Правило. С помощью циркуля и линейки можно построить любой правильный 2k-угольник, где k любое целое число, большее двух.
Интересные факты.
Семиугольник не может быть построен при помощи циркуля и линейки.
Семнадцатиугольник может быть построен с помощью циркуля и линейки.
Как построить правильный шестиугольник с помощью циркуля. Как построить правильный шестиугольник. Определение и построение
Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Результат
Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .
2. Переход между шестиугольниками
Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.
3. Делим на секции
Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому.
4. Закрашиваем секции
Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:
- Синий: C 65 M 23 Y 35 K 0
- Бежевый: C 13 M 13 Y 30 K 0
- Персиковый: C 0 M 32 Y 54 K 0
- Светло-розовый: C 0 M 64 Y 42 K 0
- Темно-розовый: C 30 M 79 Y 36 K 4
В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.
5. Последние штрихи и узор
Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B . Выровняйте группы.
Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса
Рисунок 38
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D .
Рисунок 39
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины
Рисунок 40
Остальные вершины C и F определяют с помощью дуги окружности радиуса OA , которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана.

- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Содержимое:
Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Шаги
1 Рисуем идеальный шестиугольник при помощи циркуля
- 1 При помощи циркуля рисуем круг. Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг.
- Иногда легче сначала нарисовать пол круга, а затем вторую половину.
- 2 Передвиньте иглу циркуля к краю круга. Поставьте его на вершину круга. Не меняйте угол и расположение циркуля.
- 3 Сделайте небольшую отметку карандашом на краю круга. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете. Не забудьте сохранять угол, который вы установили для циркуля.
- 4 Передвиньте иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.
- 5 Сделайте еще одну отметку карандашом на краю круга. Таким образом, вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.
- 6 Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
- 7 Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
- 8
Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали.
 После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
2 Рисуем грубый шестиугольник при помощи круглого предмета и линейки
- 1 Обведите ободок стакана карандашом. Таким образом, вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу.
- 2 Нарисуйте горизонтальные линии через центр вашего круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив его пополам.
- 3 Нарисуйте «Х» над половиной круга, разделяя его на шесть равных секций. Так как вы уже провели линию через середину круга, Х должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.
- 4 Сделайте из каждой секции треугольники. Чтобы это сделать, при помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, образовывая треугольник. Сделайте это с оставшимися пятью секциями. Думайте об этом, как об изготовлении корочки вокруг ваших кусков пиццы.
- 5 Сотрите все вспомогательные линии. К вспомогательным линиям относятся ваш круг, три линии, которые разделили ваш круг на секции и другие отметки, которые вы делали в процессе.
3 Рисуем грубый шестиугольник при помощи одного карандаша
- 1 Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку вашей горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может быть всего пара сантиметров.
- 2 Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа.
 Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии. - 3 Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом, будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
- 4 Нарисуйте еще одну горизонтальную линию, соединяя нижние две диагональные линии. Таким образом, вы нарисуете основу для своего шестиугольника. В идеале эта линия должна быть параллельной к верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.
- Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
- Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.
Предупреждения
- Циркуль — довольно острый предмет, будьте с ним очень аккуратны.
Принцип работы
- Каждый метод поможет нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон. Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.
Что вам понадобится
- Бумага
- Карандаш
- Линейка
- Пара циркулей
- Что-то, что можно подложить под бумагу, чтобы игла циркуля не соскальзывала.
- Ластик
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами.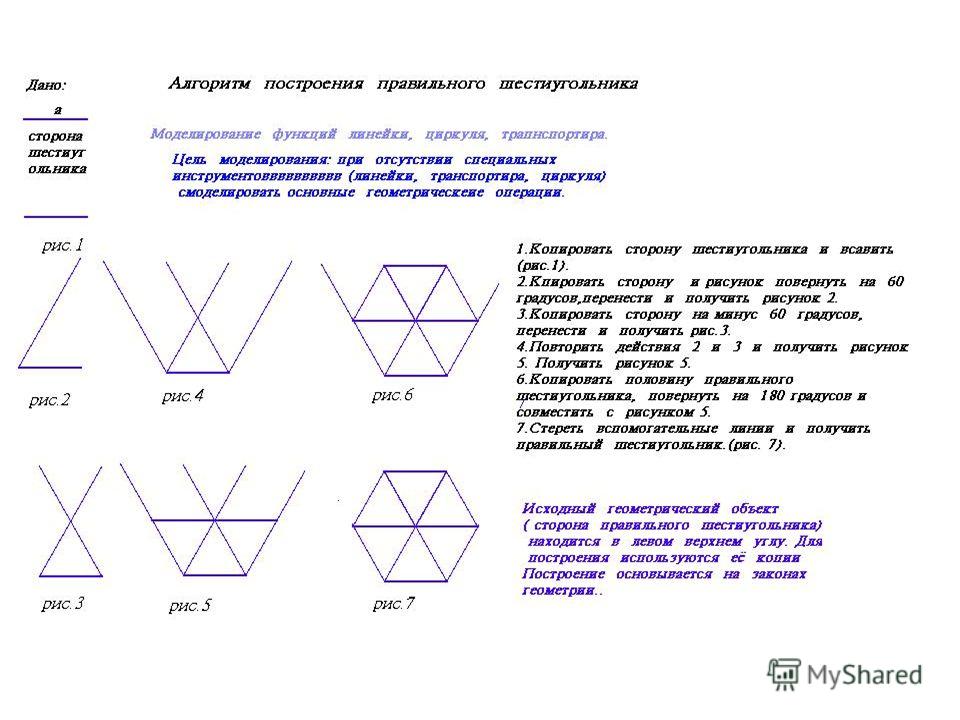 Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
- – циркуль;
- – линейка;
- – карандаш;
- – лист бумаги.
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
Построение правильных многоугольников — Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
Как рисовать правильный пятиугольник с помощью циркуля. Правильный пятиугольник. Получение с помощью полоски бумаги
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Построение вписанного в окружность правильного пятиугольника. Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Построить пятиугольник и поможет именно эта окружность. В первую очередь необходимо построить циркулем окружность. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Она и представляет собой многоугольник, остается только ввести параметры. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Деление окружности на равные части и вписывание правильных многоугольников.
Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Можно обозначить их как (0,0), но могут быть и любые другие данные. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.
В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране. Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности.
Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Окружность, дуги и многоугольники.
Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги при помощи линейки нарисуйте прямую линию выбранной длины. Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставить место для рисования других сторон). Используя транспортир, отложите угол в 135o (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом в 135o ко второй линии. Продолжайте до тех пор, пока у вас не получится правильный восьмиугольник.
Таким образом, чем больше окружность, тем больше фигура (и наоборот). Нарисуйте вторую большую окружность, установив иглу циркуля в центре первой окружности. Установите иглу циркуля в прямо противоположной точке пересечения внутренней (малой) окружности и ее диаметра. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
Построение правильных многоугольников по заданной стороне
Сотрите окружности, линии и дуги, оставив только восьмиугольник. Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.
Смотреть что такое «Правильный пятиугольник» в других словарях:
Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.
Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
Вам понадобится
- – линейка
- – циркуль
Инструкция
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.
3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Инструкция
1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).
3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .
4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .
5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.
6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.
Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .
3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.
4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Видео по теме
Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.
2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.
5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.
6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Видео по теме
Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.
Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Как начертить пятиугольник с помощью транспортира
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника
На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…
Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…
Последние события
Раскраски к Хеллоуину для мальчиков
В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.
Коллекция раскрасок к Хеллоуину
Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.
На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.
Осень. Деревья и листья
Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.
Кто такие мишки Гамми?
Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.
Несколько раскрасок для самых маленьких
Совсем простенькие раскраски с крупными деталями для самых маленьких художников.
Осеннее настроение. Раскраски
В разгаре золотая осень. В этом году она в наших краях как никогда поздняя и ослепительно красивая.
Рассказы про осень. Читаем и раскрашиваем картинки
Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.
Популярное
Архив
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.
Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Как построить шестигранник
Один из первых способов построения правильного шестиугольника описал древнегреческий ученый Евклид в своем известном труде «Начала». Предложенный Евклидом способ не единственно возможный.Вам понадобитсяРассматриваемые здесь способы построения правильного шестиугольника основаны на следующих известных утверждениях. Около всякого правильного многоугольника можно описать окружность. Сторона правильного шестиугольника равна радиусу описанной около него окружности.
Способ первый. Чтобы построить правильный шестиугольник с заданной стороной а, необходимо с помощью циркуля провести окружность с центром в точке О и радиусом R, равным стороне а. Из центра окружности в точке О проведите луч в любую точку, лежащую на окружности. На пересечении окружности и луча вы получите некоторую точку А. С помощью циркуля из точки А радиусом R, равным стороне а, сделайте на окружности засечку и получите точку В. Из точки В раствором циркуля, равным радиусу R=a, сделайте следующую засечку и получите точку С. Делая аналогичным образом на окружности последовательные засечки радиусом R, равным заданной стороне а, вы получите в общей сложности шесть точек — A, B, C, D, E, F, которые будут являться вершинами шестиугольника. Соединив их с помощью линейки, получите правильный шестиугольник со стороной, равной а.
Способ второй. Через некоторую точку А проведите отрезок KB так, что KA=AB=a. На отрезке BK, равном 2а, как на диаметре постройте полукруг с центром в точке А и радиусом, равным а. Этот полукруг поделите на шесть равных частей. Получите точки C, D, E, F, G. Центр А соедините лучами со всеми полученными точками, кроме последних двух точек — K и G. Из точки В радиусом АВ проведите дугу, делая засечку на луче АС. Получите точку L. Из точки L тем же радиусом проведите дугу, делая засечку на луче AD. Получите точку М. Аналогичным способом проводите дуги и делайте засечки для остальных точек. Точки B, L, M, N, F, A последовательно соедините прямыми линиями. Получите ABLMNF – правильный шестиугольник со стороной, равной а.
Обычное, Идеальное, От Квадрата
Как нарисовать шестиугольник? Как разделить круг на пять равных частей? Вы сможете найти ответ на все эти вопросы, если выполните эти шаги вслед за мной. Слабо определенный шестиугольник — это любой многоугольник с шестью сторонами. Однако правильный шестиугольник состоит из шести равных частей и шести равных углов.
Посмотрите на изображения шестиугольников, чтобы получить четкое представление о том, что вы рисуете. О том, как нарисовать шестиугольник и идеально правильную форму, и пойдет речь в этой статье! Нарисовать шестиугольник просто и понятно, если следовать вашим рекомендациям! В контакте, подумайте, просто начертите доступное изображение шестиугольника.
С помощью линейки и транспортира начертите идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглую форму и линейку, чтобы указать рукой. Если точность не имеет первостепенного значения, не стесняйтесь подготовить легкий шестиугольник, используя всего лишь карандаш и свое чутье. Конечно, нам понадобится циркуль с ручкой и линейкой, чтобы нарисовать красивый шестиугольник!
Чертеж идеального шестиугольника Для начала нарисуйте циркуль.
Разделите его на четыре части линиями сверху вниз и справа налево.
Сразу объясните ребенку, что отрезок, соединяющий две точки на окружности и проходящий через его центр, называется диаметром.
А отрезок, соединяющий центр и точку на окружности, называется радиусом.
Как нарисовать правильную звездочку
С помощью линейки отмерьте и разрежьте пополам одну из радиостанций.
У меня этот сегмент находится слева от центра.
Я отметил середину радиуса.
номер 1.
Нам нужна точка на вершине круга.
Я отметил его цифрой 0.
Установить стрелку компаса
до точки 1 и карандашом указать 0.
Нарисуйте дугу до пересечения с горизонтальным диаметром.
Обозначим точку пересечения
номер 2.
Теперь устанавливаем стрелку компаса.
до точки 0 и карандашом указать 2.
И нарисуйте дугу до пересечения с кругом, причем с двух сторон.
Обозначены точки пересечения.
числа 3 и 4.
Не меняя ширины циркуля, установите стрелку.
в точке 3 и отмерьте кусок круга.
Ставим точку 5.
Точку 6 можно измерить от
точки 5 и из пункта 4.
Главное не менять ширину (раствор) ножек суппорта.
Здесь почти все.
Если соединить точки, получится правильный пятиугольник. А можно звездочку нарисовать!
Вот так звездочка нарисована.
Набор для рисования с шестигранной линейкой идеально подходит для дизайнеров и мастеров
Дизайнеры, художники, архитекторы и все, кто любит рисовать или рисовать, могут быть заинтересованы в новом наборе уникальных шестиугольных линейок, созданных Yuan Design Studio. Линейки, состоящие из трех шаблонов, можно комбинировать в самых разных сценариях, чтобы получить многофункциональную металлическую линейку, которая поможет вам более эффективно рисовать идеи.
Ранние взносы теперь доступны для интересного проекта от примерно 18 долларов или 13 фунтов стерлингов (в зависимости от текущего обменного курса) , предлагая значительную скидку в размере примерно 12% от окончательной розничной цены, пока продолжается краудфандинг на Kickstarter.Если кампания «Гексагональная линейка 2.0» успешно достигнет поставленной цели и производство будет развиваться плавно, ожидается, что мировые поставки начнутся примерно в июле 2021 года. Чтобы узнать больше о проекте «Гексагональная линейка 2.0», просмотрите рекламный видеоролик ниже.
«Hexagonal Ruler впервые был запущен на Kickstarter в 2017 году, наш проект поддержали более 900 человек. Мы так благодарны, что многим из вас нравится наша концепция и дизайн. За эти 3 года мы синтезируем отзывы наших клиентов и новые идеи дизайнеров, так что мы подошли к Hexagonal Ruler 2.0. «
»«Вспышки вдохновения всегда неожиданны. Однако обычные инструменты для создания эскизов имеют большие размеры, и их нелегко использовать в общественных местах, таких как кафе или поездки на работу. Поэтому мы разрабатываем 3 линейки среднего размера для разработки идей в любое время и в любом месте. Каждая шестиугольная линейка размером всего 72×62 мм с разнообразными функциями, такими как компас, транспортир и шаблонная линейка … Сделанный на заказ футляр — это набор профессиональных инструментов на вашем пути к дизайну ».
«По сравнению с традиционными линейками, шестиугольник позволяет использовать больше функций.Вы найдете множество функций в одной шестиугольной линейке. Кроме того, пользователи могут легко положить их в карман и мгновенно использовать благодаря особой форме шестиугольника. Беспрецедентное изменение набора шестиугольной линейки объединяет все функции в 3 линейки вместо 4, что означает меньше линейок, но больше функций ».
Для получения полного списка всех доступных вариантов поддержки, растяжек, дополнительных носителей и спецификаций перейдите к официальной шестиугольной линейке 2.0, перейдя по ссылке ниже.
Источник: Kickstarter
В рубриках: Новости гаджетов, Главные новостиПоследние предложения Geeky Gadgets
Раскрытие информации: Некоторые из наших статей содержат партнерские ссылки. Если вы покупаете что-то по одной из этих ссылок, Geeky Gadgets может получать партнерскую комиссию. Узнать больше.
Нарисуйте шестиугольник с помощью циркуля для рисования — Практическое руководство
Я не могу вспомнить, изучал ли я эту технику рисования шестиугольника в начальной школе, но я определенно помню, как моя мама учила меня, делая для нас одеяло из шестиугольника … с помощью циркуля для рисования … Мой первый урок по сшиванию шестиугольника цветка Блок квилта предназначен для рисования этого картонного шаблона шестиугольника.До сегодняшнего дня я все еще слышу бормотание мамы в ушах…
«Идеальный шестигранный цветок для квилтинга получается из точных шестигранных шаблонов» … ..
Пока я не стал немного старше, я научился использовать угловую линейку, чтобы рисовать шестиугольник в моем формальном образовании, например, делить 360 ° на 6 частей по кругу и т. Д. Но мне все еще нравится способ моей мамы, с одним простым инструментом, компасом … так прямолинейно и надежно !!! Если вы используете компьютерное программное обеспечение для создания шаблона шестиугольника, это один из простейших методов….просто замените циркуль кружками.
Нарисуйте шаблон шестиугольника вашего собственного размера, используя этот урок, чтобы сделать свое лоскутное одеяло из шестиугольника.
Как нарисовать шестиугольник для лоскутного одеяла
Инструменты:
1. Циркуль
2. Карандаш (заточенный)
3. Линейка
4. Картон
5. Ножницы
Нарисуйте круг на картоне с помощью циркуля желаемого радиуса.
Радиус — это ширина одной из граней вашего шестиугольника.
Наибольшая ширина шестиугольника — это диаметр круга, который в 2 раза больше радиуса.
Отметьте произвольно первую точку на окружности.
С такими же настройками на компасе поместите стрелку компаса в 1-ю точку и отметьте вторую точку пересечения на окружности.
Поверните циркуль на другую сторону круга, отметьте третью точку пересечения.
Повторите процесс, переместив стрелку компаса на 2-ю точку и 3-ю точку, чтобы отметить 4-ю и 5-ю точки соответственно, а затем — 6-ю точку.
Вы можете выполнить контрпроверку правильности разметки, например, когда ваша стрелка находится на 2-й точке, а вы отмечаете 4-ю точку, поверните циркуль в 1-ю точку и посмотрите, касается ли карандаш той же точки.
После того, как вы отметили все 6 точек на окружности, нарисуйте отрезок прямой линии между ближайшими пересечениями. Вот ваш шестиугольник с 6 равными сегментами на круге.
Вырежьте из картона шестигранник.Используйте его в качестве шаблона и начните рисовать шестиугольники для своего проекта квилтинга.
Проверьте соответствие формы и размера. При необходимости нарисуйте еще один новый шаблон шестиугольника, если первый изношен после выполнения некоторых начертаний.
Нарисуйте еще один шаблон побольше для ткани. Добавьте еще от 1/2 ″ до 3/4 ″ к радиусу шаблона ткани, повторите технику рисования шестиугольника, чтобы создать шаблон ткани. Вам понадобится всего несколько штук, чтобы просто нарисовать шестиугольники на ткани.
Шестиугольники разных размеров, от 1 до 3 дюймов в ширину.
Возьмите достаточно их (1 размера) для запланированного проекта квилтинга и сшейте их вместе.
Построение правильных многоугольников
«ВОЗВРАЩАТЬСЯ» Copyright 2001 & nbsp & nbsp & nbsp 1728 Software Systems |
Быстрый и легкий шестигранный блок с 60-градусной линейкой видеоурок
Я обнаружил новый тип блока, который изготавливается с помощью 60-градусной линейки или шаблона. Вы фактически делаете 2 разных блока одновременно с помощью этой техники, которые могут быть выложены как 2 отдельных шестиугольных блока или как один соединенный блок, как в этом случае.
Если у вас нет линейки с углом 60 градусов, вы можете скачать выкройку:
Если вы планируете резать под углом 60 градусов, вы можете подумать о приобретении линейки с углом 60 градусов.
Материалы
Отрежьте 3 полосы ткани:
- 37 X 3 1/4 дюйма красного цвета
- 37 X 2 3/4 дюйма синего цвета
- 37 X 1 дюйм, уголь
Отрежьте еще 3 полоски ткани:
- 21 X 3 1/4 дюйма красного цвета
- 21 X 2 3/4 дюйма синего цвета
- 21 X 1 дюйм, уголь
Эти 2 полоски образуют по 6 треугольников каждого типа с перевернутыми полосками ткани.
Готовый размер
Как 2 чересстрочных блока: 11 дюймов x 18 1/2 дюймов (всего 10 треугольников, по 5 каждого типа).
В виде 2 отдельных блоков: 11-дюймовый квадрат (всего 6 треугольников, по 6 каждого типа).
Как сделать этот шестигранный блок с помощью линейки на 60 градусов
Посмотрите, как легко можно сделать блоки шестиугольника из равносторонних треугольников:
Если у вас нет линейки с углом 60 градусов
Не волнуйтесь, вот как вырезать треугольники с углом 60 градусов без специальной линейки:
Если вам нравятся мои видео, подпишитесь на мой канал.Если вы сделаете какие-либо из моих руководств и загрузите фотографии в Instagram, отметьте меня @teresadownunder
Нравится ли вам этот блок?
Вы можете сделать полное лоскутное одеяло из этих блоков и еще 9 макетов шестиугольных блоков с моим лоскутным одеялом «Гексагональная мечта».
Купите выкройку в моем магазине Etsy.
Визуальный процесс
Нравится:
Нравится Загрузка …
Связанные Выкройка для квилтинга с треугольными полосками под 60 градусов видеоурокНарисуйте шестиугольник
Как нарисовать шестиугольник — youtube
Как нарисовать шестиугольник шаг за шагом для детей, Спасибо за просмотр нашего канала.Как нарисовать шестиугольник шаг за шагом для детей, как нарисовать шестиугольник без циркуля, как нарисовать шестиугольник, как нарисовать он
как нарисовать шестиугольник., Шестиугольник | Нарисуйте шестиугольник | Инженерный рисунок. Почему люди считают, что они не умеют рисовать, и как доказать, что они умеют | Грэм Шоу | TEDxHull — Продолжительность: 15:04. TEDx Talks Рекомендуется для вас
Как нарисовать идеальный шестиугольник, Привет, Гиз .. Это учебное пособие по геометрической работе с изображением с помощью MATLAB.. Итак, здесь мы узнаем о том, как нарисовать шестиугольник с помощью MATL
.Как нарисовать восьмиугольник
Как нарисовать восьмиугольник (с изображениями), прямая вертикальная линия (также разделяющая круг на равные части), центр которой будет пересекаться с центром горизонтальной линии. Множественный восьмиугольник 1. Нарисуйте квадрат в центре страницы. 2. Нарисуйте прямые линии, которые соединят один угол с его прямым противоположным углом. 3. Отметьте расстояние от центральной точки (где линии пересекаются) до одного из углов квадрата.4. Обратите внимание на точку, где находится круг и
, как нарисовать восьмиугольник с циркулем и линейкой, Шаг 3: сделайте восьмиугольник из 9 квадратов. Сделайте восьмиугольник из 9 квадратов. Нарисуйте линии так, чтобы получился восьмиугольник. Нарисуйте линию между двумя метками, ближайшими к каждому углу, и сотрите углы квадрата и букву «X», чтобы завершить равносторонний восьмиугольник. КАК ЭТО РАБОТАЕТ: Используя теорему Пифагора, которая составляет A² + B² = C², вычислите длину гипотенузы, или «C» на рисунке. Длина одной стороны квадрата составляет 5 дюймов, поэтому 1/2 этой длины составляет 2-1 / 2 дюйма.
Как нарисовать восьмиугольник в квадрате, Нарисуйте правильный восьмиугольник, используя шаблон жесткого квадрата, прямой край и карандаш или ручку. Задача, поставленная в заголовке этих инструкций, может заключаться в том, чтобы нарисовать квадрат, то есть используется для рисования этого восьмиугольника.
Нарисуйте шестиугольник онлайн
Бесплатный онлайн-генератор шестиугольника, Используйте этот бесплатный онлайн-генератор шестиугольника для создания шаблонов шестиугольника. Рисуя шаблон прямо на листе сушилки, пришейте прямо к ткани, используя «Нарисовать шестигранный график».Онлайн-калькулятор для построения графиков, позволяющий изобразить / нарисовать фигуру шести (6) стороннего многоугольника / шестиугольника с заданным радиусом. С помощью этого графического онлайн-калькулятора рисовать шестиугольник стало проще.
Калькулятор шестиугольника, Размер шестигранника: дюймы, см. Добавить точку: поставьте точку в середине каждого шестиугольника. Цвет: Hex # Вычисление различных бит о правильных шестиугольниках. Заданная длина. Для случайного (неправильного) шестиугольника ответ прост: нарисуйте любую 6-стороннюю форму так, чтобы она была замкнутым многоугольником, и все готово.Но с правильным шестиугольником все не так просто, так как мы должны убедиться, что все стороны имеют одинаковую длину. Для получения идеального результата вам понадобится циркуль для рисования. Нарисуйте круг и с тем же радиусом запустите
Бесплатная онлайн-миллиметровка / шестиугольник, Калькулятор шестиугольника. Расчеты на правильном шестиугольнике, многоугольнике с 6 вершинами. Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику. Как нарисовать шестиугольник и его идеально правильную форму, мы обсудим в этой статье! Нарисовать шестиугольник просто и понятно, если следовать вашим рекомендациям! В контакте, подумайте, просто начертите доступное изображение шестиугольника.Примените линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Для более грубого шестиугольника попробуйте использовать круглую форму и линейку
Как нарисовать шестиугольник на миллиметровой бумаге
Нарисовать шестиугольник намного проще, если вы рисуете его на миллиметровой бумаге внутри сетки размером четыре на четыре . Картинка стоит тысячи слов, вот и одно: секрет здесь не в подсчете квадратов, а в пересчете миллиметровой бумаги. Как только вы это сделаете, шестиугольник будет красиво рисоваться из четных точек.
Если у вас нет циркуля, вы можете нарисовать шестиугольник другим способом, для чего потребуется миллиметровая бумага.Шаг 1 Нарисуйте точку на пересечении двух линий на миллиметровой бумаге.
Как нарисовать правильный шестиугольник на миллиметровой бумаге Сэди Мерфи — 8 апреля 2015 г. — как нарисовать правильный шестиугольник на миллиметровой бумаге
Различные формы шестиугольника
Geometry at Amazon®, Shop Devices, Apparel, Books, Музыка и многое другое. Быстрая бесплатная доставка квалифицированных заказов. В геометрии шестиугольник (от греческого ἕξ hex, «шесть» и γωνία, gonía, «угол, угол») представляет собой шестиугольник или шестиугольник.Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
Шестиугольник | Что такое шестиугольник, В геометрии многоугольник — это любая двумерная форма, которая соответствует требованиям. Имена сложных многоугольников иногда отличаются от имен этих шестиугольников. Эти формы шестиугольников идеально подходят для использования с English Paper Piecing. Просто заверните их в свои любимые лоскутки ткани и прострочите вместе, чтобы получить быстрые и легкие подарки, такие как эта тетрадь для рукоделия. Если вы новичок в EPP, ознакомьтесь с нашим Руководством для начинающих, чтобы научиться основам.
Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны, В геометрии шестиугольник — это шестиугольник или шестиугольник. Сумма внутренних углов any и r12, как параллелогонов, может разбить на мозаику евклидову плоскость путем перевода. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией. Изображение шестиугольника. На этой картинке изображен шестиугольник. Шестиугольник — это многоугольник с 6 сторонами и 6 внутренними углами, которые в сумме составляют 720 градусов. Наслаждайтесь рядом бесплатных изображений с многоугольниками и многогранниками всех форм и размеров, включая простые 2D-формы, 3D-изображения, звезды и кривые, прежде чем переходить наш раздел фактов о геометрии, чтобы узнать о них все.
Как нарисовать шестиугольную призму
3 способа нарисовать шестиугольную призму, Как нарисовать шестиугольную призму. Вы хотите научиться рисовать шестиугольную призму? Из этой статьи вы узнаете, как легко сделать любую призму! Как нарисовать шестиугольник шаг за шагом легко для детей / начинающих — Урок по рисованию простого шестиугольника — Продолжительность: Как сделать пятиугольную призму — Продолжительность: 8:56. Инструменты интеллектуального обучения 26 840 просмотров.
Как нарисовать шестиугольник шаг за шагом для детей / начинающих, Этот урок является подготовительным к рисованию правильной шестиугольной призмы в следующем уроке.Поместите большую правильную шестиугольную плоскость, вырезанную из жесткого или тонкого картона. Когда призма расположена горизонтально, как на рис. 70, 71 и 72, нарисуйте видимый конец, как описано ранее, для вертикальной правильной шестиугольной плоскости. Затем нарисуйте края 9–10, I –11, 8–12 и 6–13 с правильным кажущимся наклоном и сравнительной длиной по сравнению с вертикальной линией 8–9, которая может иметь длину около двух с половиной дюймов.
нарисовать шестиугольную призму, Как нарисовать шестиугольную призму? इस видео में हम Гексагональная призма के बारे में बताया है। устанавливается с помощью setdrawing.Пропустить навигацию Войдите.
Как нарисовать пятиугольник
Пентагон, горизонтальную линию, проходящую через центр круга. Как нарисовать идеальный пятиугольник 1. Первый шаг к рисованию идеального пятиугольника — это отметить точку в центре листа. Поместите циркуль на 2. Используя центральную точку и транспортир, разделите круг на 5 точек. В круге 360 °, а 360/5 = 72 °. 3. Соедините каждый соседний
, как нарисовать пятиугольник без использования транспортира, Постройте точку M как среднюю точку O и B.Рисование пятиугольника. Шаг 1 :. Сначала нарисуйте горизонтальные и вертикальные линии. Шаг 2:. Затем нарисуйте круг с центром в перекрестии. Не складывайте циркуль после того, как нарисован круг. Сторона Шага 3 :. Не регулируя компас, поместите точку циркуля на круг, где он пересекает
Как нарисовать правильный пятиугольник, зная длину одной стороны, Рисование пятиугольника: Это дополнение к проекту календаря Додекаэдра. Здесь я демонстрирую, как нарисовать идеальный пятиугольник.Вам понадобится линейка и как нарисовать пятиугольник без использования транспортира или углового инструмента. Пентагон — это геометрическая форма, у которой 5 равных сторон и 5 углов. Это лучший и простой урок
Как нарисовать шестиугольник с помощью заданного квадрата
Построение шестиугольника с использованием квадрата 60 ° (PLA / A2), Используйте линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглый. Нарисовать шестиугольник просто и понятно, если вы будете следовать своим рекомендациям! В контакте, подумайте, просто начертите доступное изображение шестиугольника.Примените линейку и транспортир, чтобы нарисовать идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглую форму и линейку, чтобы указать рукой. Если точность не имеет первостепенного значения, не стесняйтесь подготовить легкий шестиугольник, используя всего лишь карандаш и свое чутье.
Как нарисовать шестиугольник с помощью заданных квадратов, Нарисуйте вертикальный диаметр AB и используйте T-квадрат и треугольник 30 ° / 60 °, чтобы провести BC от B под углом 30 ° к горизонтали. Установите компас на BC, отложите ШАГ 1: Используя карандаш и линейку, проведите горизонтальную линию.Установите циркуль на ширину линии. Поместите циркуль на обоих концах линии и нарисуйте две дуги, пересекающиеся посередине. 3 из 9
Как нарисовать шестиугольник., Чтобы нарисовать шестиугольник, учитывая расстояние по углам 2 С установленным квадратом 60 ° нарисуйте точки на окружности, разнесенные на 60 °. 2 Разделите полукруг на семь равных углов, используя транспортир, и через второй. Постройте правильный 5-сторонний многоугольник с учетом измерения одной из его сторон, используя циркуль и установленный квадрат 45º.Этот канал на YouTube посвящен
Другие статьи
Свойства калькулятора шестиугольника и правильного шестиугольника
Теоретические основы
Оглавление
Определения
Шестиугольник — это многоугольник с шестью сторонами и шестью вершинами. Как и любой многоугольник, шестиугольник может быть выпуклым или вогнутым, как показано на следующем рисунке. В выпуклом состоянии шестиугольник (или многоугольник в целом) не имеет внутренних углов больше 180 °.Напротив, вогнутый шестиугольник (или многоугольник) имеет один или несколько внутренних углов больше 180 °. Шестиугольник называется правильным, если все его стороны и внутренние углы равны . В отличие от треугольника, наличие равных сторон не означает, что внутренние углы также равны, поскольку шестиугольник может быть вогнутым. Как показано на рисунке ниже, можно определить множество возможных вогнутых шестиугольников с равными сторонами, но с разными внутренними углами (они называются равносторонними). Неправильный шестиугольник называется неправильным.
Типы шестиугольниковСумма внутренних углов любого шестиугольника, выпуклого или вогнутого, всегда равна 720 °. В этом легко заключить, посчитав количество треугольников, помещающихся внутри шестиугольника, соединив его вершины (избегая пересечений). Действительно, есть 4 треугольника. Так как сумма внутренних углов в одном треугольнике равна 180 °, четыре треугольника, расположенные рядом, должны иметь размер 4×180 = 720 °.
Диагонали шестиугольника разделяют его внутреннюю часть на 4 треугольника.Свойства правильных шестиугольников.
Симметрия
Правильный шестиугольник имеет шесть осей симметрии.\ circ
Два оставшихся угла в треугольнике также равны 60 °. На самом деле это \ varphi / 2, потому что диагонали шестиугольника (линии, соединяющие противоположные вершины) также являются осями симметрии, таким образом разделяя внутренний угол \ varphi пополам (который составляет 120 °). Следовательно, все шесть треугольников, у которых центр шестиугольника является одной из вершин, являются идентичными равносторонними треугольниками.
Внутренний и центральный углы также являются дополнительными, поскольку их сумма равна 180 °:
\ varphi + \ theta = 120 ° + 60 ° = 180 °
Правильный шестиугольник состоит из шести одинаковых равносторонних треугольников, имеющих общую вершину, центр многоугольника. {\ circ}}}
Аппроксимация последнего уравнения:
A \ приблизительно 2.2
Периметр любого N-стороннего правильного многоугольника — это просто сумма длин всех сторон: P = N a. Следовательно, для правильного шестиугольника:
P = 6a
Ограничивающая рамка
Ограничивающая рамка плоской формы — это наименьший прямоугольник, который полностью охватывает форму. Размеры этого прямоугольника определяются высотой h и t шириной w правильного шестиугольника.
Высота
Высота h правильного шестиугольника — это расстояние между двумя противоположными краями.\ circ}
, что приблизительно равно:
h \ приблизительно 1,732 R_c
h \ приблизительно 1,732 a
Ширина
Ширина w — это расстояние между двумя противоположными вершинами правильного шестиугольника (длина его диагонали) . Это равно удвоенному радиусу описанной окружности R_c:
w = 2R_c
Поскольку R_c = a, мы могли бы также написать:
w = 2a
Как нарисовать правильный шестиугольник
Вы можете нарисовать правильный шестиугольник заданная длина стороны \ alpha, используя только линейку и циркуль.Выполните шаги, описанные ниже:
- Сначала просто нарисуйте линейный сегмент, длина которого равна желаемой длине стороны шестиугольника \ alpha.
- Затем постройте окружность, имеющую центр на одном конце линейного сегмента и радиус, равный длине сегмента.
- Не меняя радиуса, постройте вторую окружность с центром на другом конце линейного сегмента. Определены две точки, где этот круг пересекается с первым.
- Используя тот же радиус, поместите кончик циркуля в любую из последних определенных точек и постройте новый круг.Новая точка определяется на пересечении с первым кругом.
- Повторите ту же процедуру еще два раза. Поместите кончик циркуля в последнюю точку и постройте новый круг. Новая точка определяется на пересечении с первым кругом.
- На данный момент определены шесть точек вокруг первого круга.

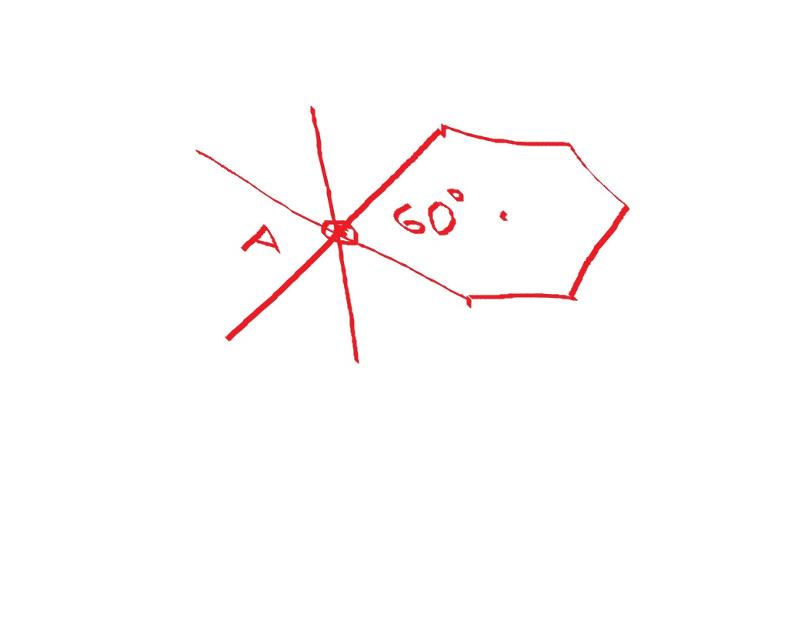 Сумма всех внутренних углов: 108*5 = 540 градусов.
Сумма всех внутренних углов: 108*5 = 540 градусов.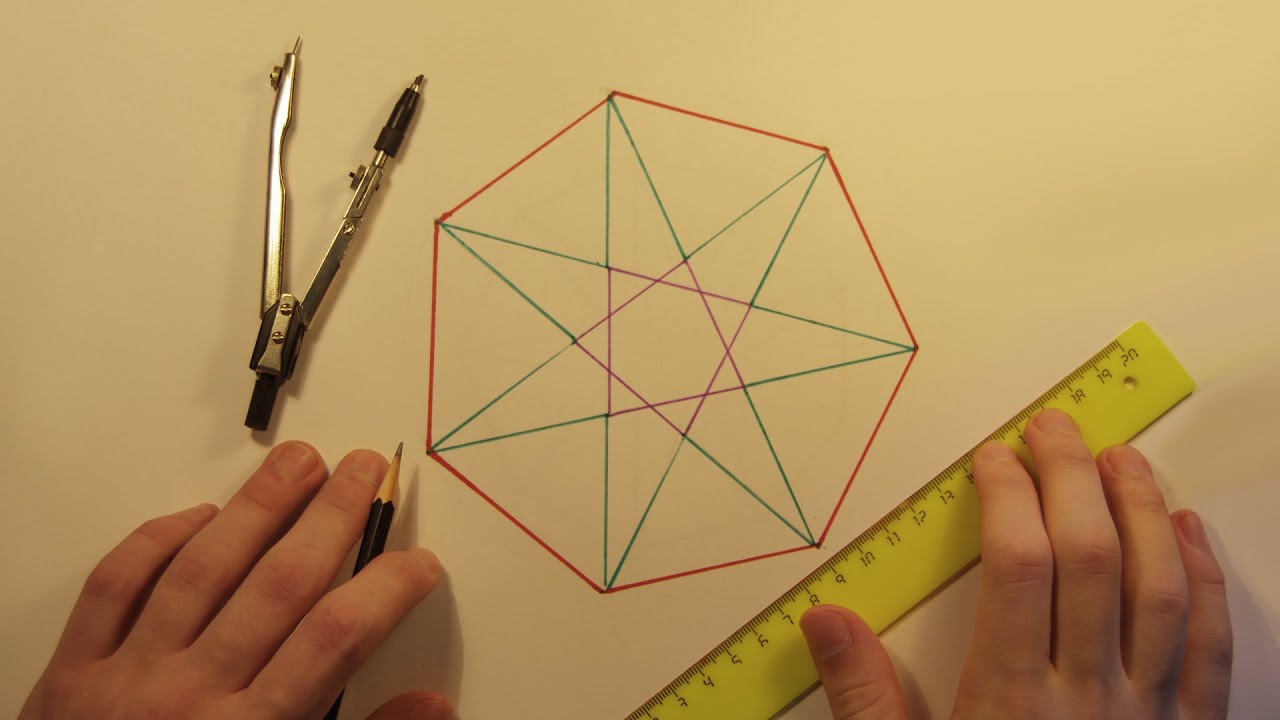
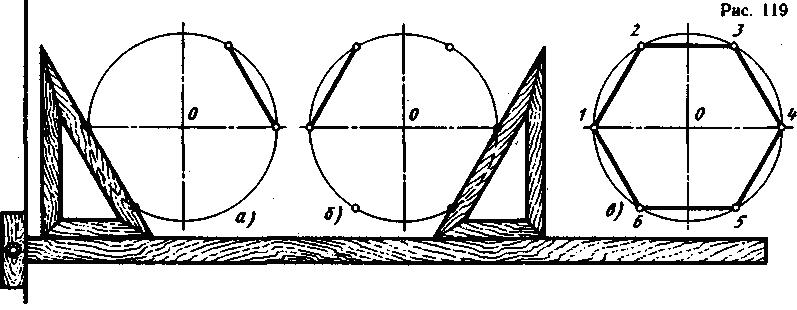
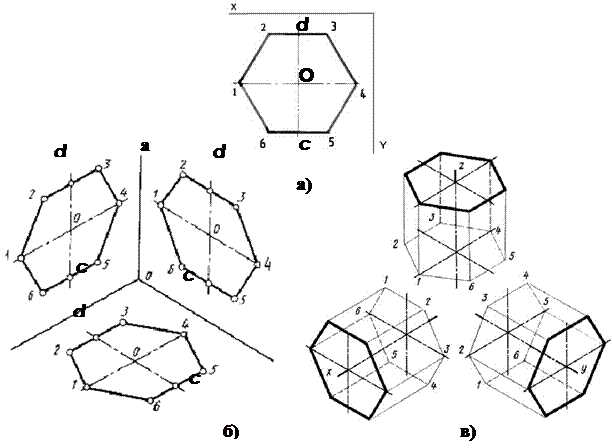 После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.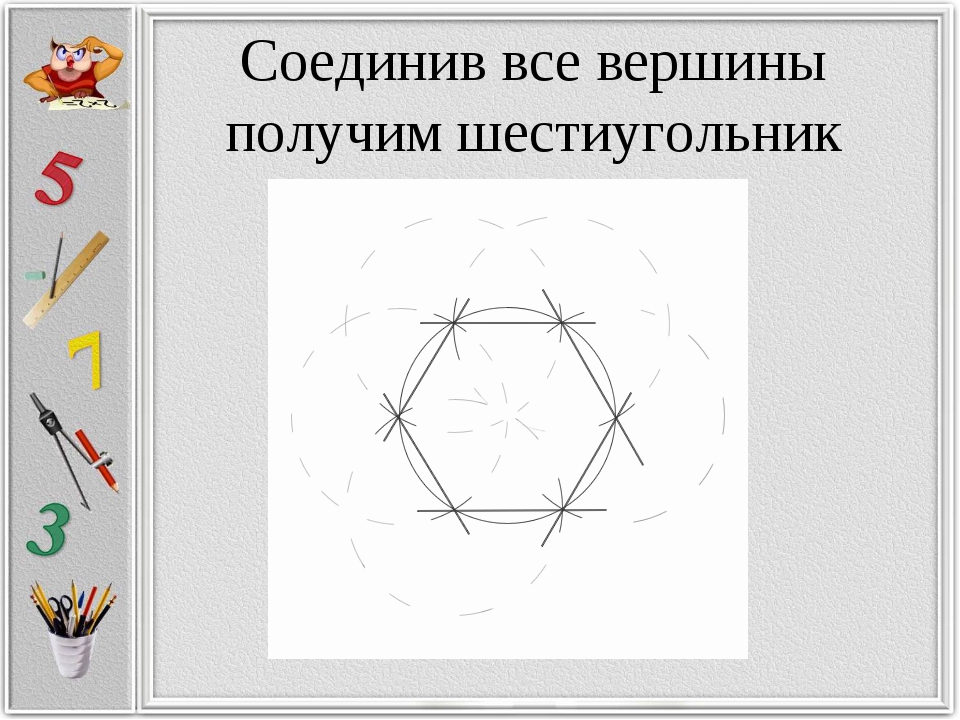 Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.