%d0%bc%d0%bd%d0%be%d0%b3%d0%be%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки

естественный цвет bb крем цвета

1200*1200

green environmental protection pattern garbage can be recycled green clean

2000*2000

набор векторных иконок реалистичные погоды изолированных на прозрачной ба

800*800

blue series frame color can be changed text box streamer

1024*1369

чат комментарий образование синий значок на абстрактных облако сообщение

5556*5556

chinese wind distant mountain pine tree chinese style pine tree chinese style poster can be combined

3600*2475

сердце сердцебиение любовь свадьба в квартире цвет значок векторная icon

5556*5556

витамин b3 ниацин вектор витамин золото масло таблетки значок органический витамин золото таблетки значок медицина капсула золотое вещество для красоты косметическое здоровье промо реклама дизайн 3d комплекс витаминов иллюстрация

5000*5000

black and white train icon daquan free download can be used separately can be used as decoration free of charge

2000*2000

в первоначальном письме векторный дизайн логотипа шаблон

1200*1200

be careful of road slip warning signs fall warning signs character warning signs pattern warning signs

2000*2000

схема бд электронный компонент технологии принципиальная схема технологическая линия

2000*2000

be careful with fire pay attention to fire pay attention to fire warning icon

2000*2000

childrens day childrens day border childrens day cute border can be used for childrens day theme poster stickers

842*596

Крутая музыка вечеринка певца креативный постер музыка Я Май Ба концерт вечер К

3240*4320

happy singing mai ba sing self indulgence happy singing

2000*2000

2022 календарь bd с фоторамкой

2500*2500

Креативное письмо bb дизайн логотипа черно белый вектор минималистский

1202*1202

Золотая буква b логотип bc письмо дизайн вектор с золотыми цветами

8334*8334

bb крем ню макияж косметика косметика

1200*1500

Реклама продукта по уходу за кожей черного золота bb bb крем bb кремовый

3240*4320

prohibited use mobile phone illustration can not be used

2048*2048

облака комиксов

5042*5042

цвет перо на воздушной подушке bb крем трехмерный элемент

1200*1200

attention be careful cut icon danger

2500*2000

be careful to slip fall warning sign carefully

2500*2775

international is not on the same day male and female couples can be commercial commercial

2000*2000

надпись laa ba sa thohurun ​​insya allah

1200*1200

элегантный серебряный золотой bb позже логотип значок символа

1200*1200

в первоначальном письме bd логотипа

1200*1200

в первоначальном письме bd шаблон векторный дизайн логотипа

1200*1200

have electricity prohibit be careful be

2000*2000

bc логотип шаблон

1200*1200

bb крем тень вектор

1300*1300

logo design can be used for beauty cosmetics logo fashion

1024*1369

желтые глаза напуганы комикс мультфильм

5000*5000

сложный современный дизайн логотипа с биткойн символами и буквами bc

8331*8331

big cock detailed layered can be used directly cock big cock chicken

2000*2000

две бутылки косметики жидкая основа белая бутылка крем bb

2000*2000

starry texture border dialog which can be used to enter borders dialogs small fresh

3600*1767

be careful of electric shock signs warning signs warnings

2000*2000

в первоначальном письме bd шаблон векторный дизайн логотипа

1200*1200

логотип готов использовать год до н э

6667*6667

be careful and fragile warning signs round beware

2500*2000

pop be surprised female character

2000*2000

простая инициализация bb b геометрическая линия сети и логотип цифровых данных

2276*2276

bc beauty косметический логотип дизайн вектор

8542*8542

в первоначальном письме bd логотип шаблон

1200*1200

hand painted chinese style pine ink ink graphics can be combined hand painted pine chinese style

2475*3600

printing type can not be separated color chart psd white cmyk

1024*1369

нереальная математика реального мира / Хабр

Математика даёт нам точное представление о почти точных ответах

Используя плотную бумагу и прозрачную ленту, Крэйг Каплан собирает красивый округлый объект, напоминающей творение Бакминстера Фуллера или модный новый тип футбольного мяча. Он состоит из четырёх правильных додекагонов (12-угольников с одинаковыми углами и сторонами) и 12 декагонов (10-сторонних многогранников) с 28 небольшими проёмами в виде равносторонних треугольников. Есть только одна проблема – эта фигура не может существовать. Такой набор полигонов не совпадёт вершинами, и фигура не закроется.

Модель Каплана работает лишь потому, что когда вы собираете её из бумаги, у вас есть небольшая свобода манёвра. Стороны могут почти незаметно изгибаться. «Запас на ошибку, возникающий из-за работы в реальном мире с бумагой, означает, что те вещи, которые не должны быть возможными, в реальности получаются», – говорит Каплан, специалист по информатике из Университета Ватерлоо в Канаде.

Это новый пример из класса неожиданных математических объектов, на которые в 1960-х случайно наткнулся американский математик Норман Джонсон. Джонсон работал над завершением проекта, начатого более 2000 лет назад Платоном – он создавал каталог идеальных геометрических фигур.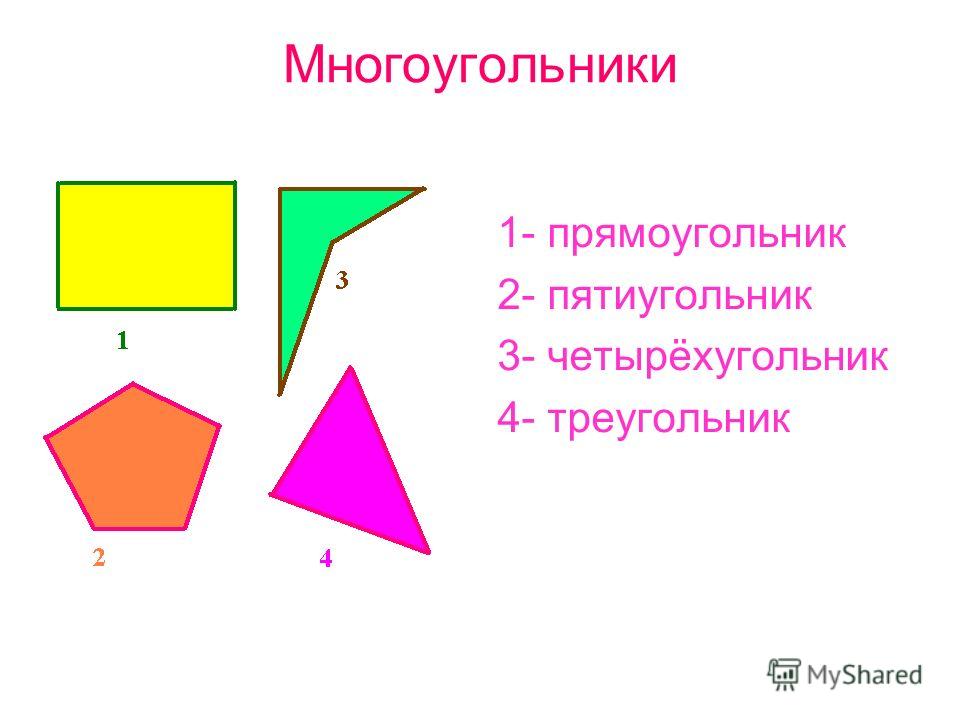 Из всего бесконечного многообразия трёхмерных фигур только пять можно создать из одинаковых правильных многоугольников: тетраэдр, октаэдр, гексаэдр, икосаэдр, додекаэдр. Если смешать различные правильные многоугольники, можно составить ещё 13 фигур, в которых все многоугольники встречаются вершинами – архимедовы тела – а также призмы (два одинаковых многоугольника, соединённые квадратами) и «антипризмы» (два одинаковых многоугольника, соединённые равносторонними треугольниками).

В 1966 году Джонсон, работая в Университете штата Мичиган, обнаружил ещё 92 тела, состоящих только из правильных многоугольников, которые сейчас [в США] называют джонсоновыми телами. И это исчерпало все возможности, что доказал несколькими годами позже русский математик Виктор Абрамович Залгаллер, работавший тогда в Ленинградском государственном университете. Никакую другую закрытую фигуру из правильных многоугольников составить невозможно.

Но во время инвентаризации многогранников Джонсон заметил нечто странное.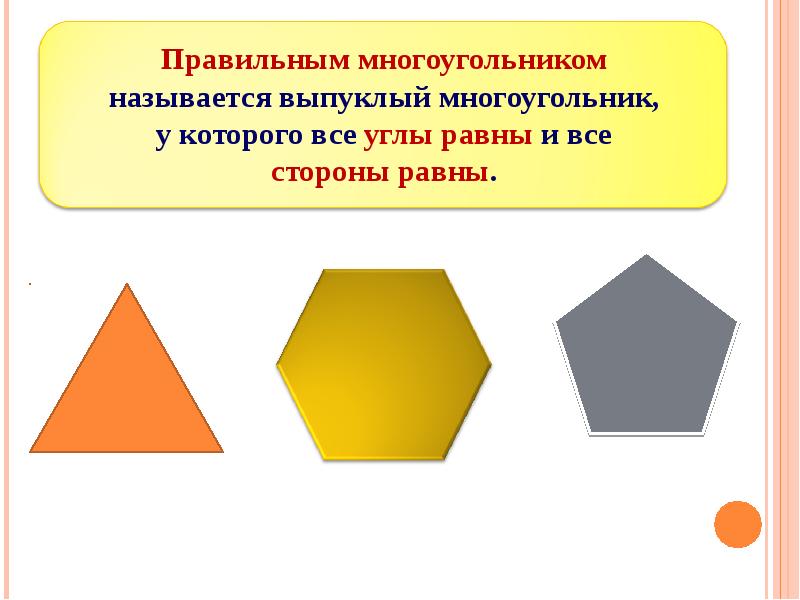 Он находил свои формы, составляя их модели из картона и резинок. Поскольку возможных многогранников довольно мало, он ожидал, что новые формы проявятся довольно быстро. Если начать составлять грани вместе, то фигура обязательно должна совпасть. Но этого не происходило. «При сборке кучи многоугольников было не всегда очевидно, собрал ли я допустимую фигуру», – вспоминает Джонсон.

Может казаться, что модель собралась, но «если провести подсчёты, оказывается, что это не совсем так», – говорит он. При тщательном изучении оказывалось, что то, что казалось квадратом, было не совсем квадратом, или стороны были не совсем плоскими. Можно было бы слегка подрезать грани, и они совпали бы идеально, но тогда это были бы уже не правильные многоугольники.

Вознамерившись подсчитать все идеальные фигуры, Джонсон не придавал значения таким «близким попаданиям». «Я отложил их, и сконцентрировался на допустимых», – говорит он. Но эти почти идеальные фигуры не только привлекли внимание Каплана и других любителей математики, они стали частью более крупного раздела почти идеальной математики.

Точного определения «почти точного» попадания не существует. Строгие правила не работают в позволяющем допуски мире. Сейчас Каплан в поиске почти правильных фигур руководствуется приближённым методом: «реальная, математическая ошибка, присущая фигуре, сравнима с практической ошибкой, возникающей из-за работы с материалами реального мира и несовершенными руками». Иначе говоря, если вам удалось собрать невозможный многогранник – если он настолько близок к возможному, что вы можете выдать его за настоящий – тогда это и будет почти точная фигура. В других разделах математики почти точные результаты оказываются так близко к реальным, что могут обмануть или удивить вас – своего рода математическая шутка.

Некоторые такие математические курьёзы нельзя назвать чем-то большим, чем простой забавой, другие же могут иметь глубинные значения в математике и физике.

Древние задачи квадратуры круга и удвоения куба попадают в категорию почти правильных решений. Они кажутся соблазнительно открытыми для нахождения правильного решения, но в итоге оказываются невозможными – как геометрическая фигура, которая выглядит закрытой, но ею не является. Некоторые конструкции, нарисованные Леонардо да Винчи и Альбрехтом Дюрером, слегка искривляли углы, выдавая почти правильные пятиугольники за настоящие.

А ещё есть загадка с пропавшим квадратом. На рисунке прямоугольный треугольник разрезан на четыре части. Если переставить их местами, в нём появляется разрыв. Откуда он взялся? Это тоже почти правильное решение. Ни один из треугольников на самом деле не треугольник. Их гипотенузы искривлены, и это почти невозможно заметить, из-за чего иллюзия настолько убедительна.

Цифровое совпадение – это одно из самых полезных в обычной жизни почти правильных решений. 2^7/12 почти равно 3/2. По схожей причине у фортепьяно есть 12 клавиш в октаве и в основе равномерно темперированного строя западной музыки. Это компромисс между двумя самыми важными музыкальными интервалами: октавой (частотой 2:1) и квинтой (частотой 3:2). Численно невозможно разделить октаву так, чтобы все квинты были идеальными. Но можно подойти к этому достаточно близко, разделив октаву на 12 полутонов, семь из которых дадут вам частоту в 1,498. Для большинства людей этого достаточно.

Иногда почти точные попадания возникают в математике так, будто она сама себя обманывает. В эпизоде Симпсонов «Treehouse of Horror VI» интересующиеся математикой зрители заметили нечто необычное: уравнение 1782¹² + 1841¹² = 1922¹². На первый взгляд может показаться, что сценаристы опровергли Великую Теорему Ферма, постулирующую, что у уравнения xⁿ + yⁿ = zⁿ не существует целочисленных решений при n > 2. Если ввести эти числа в карманный калькулятор, результат покажется вам верным. Но если провести вычисления с точностью, недоступной для большинства карманных калькуляторов, окажется, что корень 12 степени от левой части уравнения равен 1921,999999955867 а не 1922, и Ферма может быть спокоен. Удивительно маленький промах – менее, чем на 10 миллионных частей.

Но такие почти точные попадания – не просто шутки. «Те, что более других интригуют меня, это случаи, намекающие на наличие чего-то более значительного», – говорит Джон Баез, математик из Калифорнийского университета в Риверсайде. Таков случай величины, которую иногда называют константой Рамануджана. Это число e^{π √163}, равное примерно 262 537 412 640 768 743.99999999999925 – удивительно близко к целому. Мы не можем ожидать, что эти три иррациональных числа – e, π, и √163 – каким-то образом скомбинируются и дадут нам рациональное число, не говоря уже о целом. Но есть причина тому, что они так хорошо совпадают. «Это не простое совпадение, о котором мы не имеем понятия, – говорит Баез. – Это ключ к глубинам математики». Точное объяснение довольно сложное, но основывается на том, что 163 – это наибольшее из чисел Хегнера. Экспоненты, связанные с этими числами, очень близки к целым.

Или взять математическую связь, известную как «Гипотеза монструозного вздора» (monstrous moonshine). История такая: в 1978 году математик Джон Маккей сделал насколько тривиальное, настолько же и интересное наблюдение: 196 884 = 196 883 + 1. Первое число было коэффициентом важного полинома, j-инварианта, а второе возникло в связи с огромным математическим объектом из теории групп под названием «Монстр». Многие люди пожали бы плечами и пошли дальше, но это наблюдение заинтересовало многих математиков, решивших изучить его поближе. Они обнаружили связь между двумя вроде бы несвязанными темами: теорией чисел и симметрией групп Монстр. Эта связь может обладать ещё более широкими, пока не открытыми, последствиями для других тем. Физик Эдвард Уиттен считает, что группа Монстр может быть связанной с квантовой гравитацией и структурой пространства-времени.

Математические почти правильные попадания показывают как игривость, так и мощь человеческого подхода к математике. Джонсон, Каплан и другие делали открытия при помощи проб и ошибок – изучая область, как биолог, продирающийся через джунгли в поисках новых видов. Но в математике проще бывает вести систематический поиск. К примеру Джим Макнил, интересующийся математикой в качестве хобби и собирающий коллекцию почти правильных попаданий на своём сайте, и Роберт Уэбб, программист, создали ПО для создания и изучения многогранников.

Почти точные попадания живут на размытой границе между идеалистической, жёсткой математикой и нашими снисходительными и практическими чувствами. Они выворачивают наизнанку логику приближения. Обычно реальный мир считается несовершенной тенью мира Платона. Совершенство лежащей в основе математики теряется при её реализации. Но в случае почти точных попаданий реальный мир – это идеальная тень неидеального мира. Аппроксимация – это «неправильное приближение правильного ответа», говорит Каплан, а «почти точное попадание – это точное представление почти точного ответа».

Таким способом почти точные ответы меняют связь математиков и математических физиков с природой. «Я благодарен за несовершенства реального мира, поскольку они позволяют мне достигать квазиидеала, работая с объектами, по сути своей неидеальными, – говорит Каплан. – Они позволяют мне преодолевать ограничения математики благодаря красоте сломанной реальности».

Как работает модуль «Дополнительные слои» в ПК-версии — Помощник 2ГИС

С помощью дополнительных модулей можно расширить функциональность программы, подключая к ней новые модули на ваш выбор.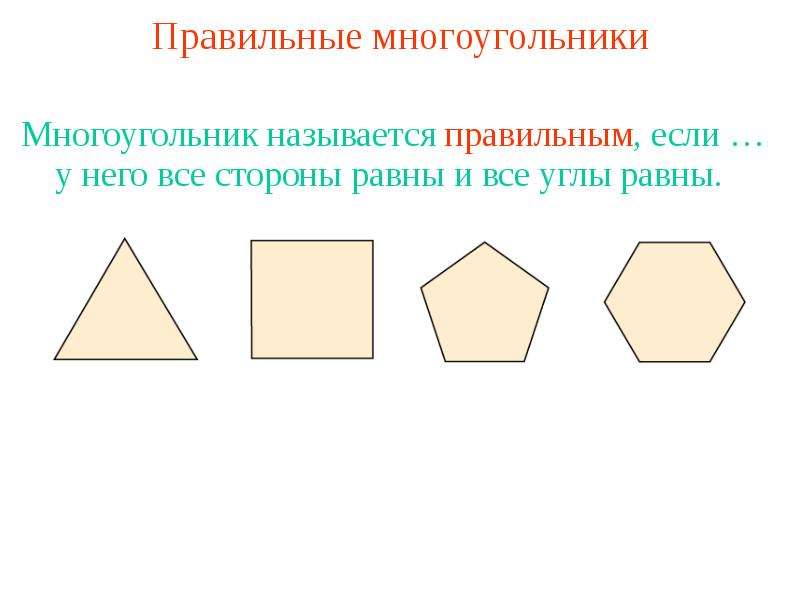 Последние версии модулей можно бесплатно скачать на странице загрузок.

Для отображения списка подключенных модулей, нажмите кнопку «Параметры» в правой верхней части окна программы и выберите пункт «Дополнительные модули».

В открывшемся окне «Дополнительные модули» можно настроить подключенные модули, нажав кнопку «Настроить», а также включить или выключить необходимый модуль.

Mодуль «Дополнительные слои» позволяет создавать, хранить и редактировать дополнительные слои на карте.

Список слоев, объектов, инструменты их создания, редактирования, сохранения собраны в едином справочнике «Дополнительные слои».

Основная часть справочника — список, который показывает текущую структуру слоев и объектов, некоторую их атрибутивную информацию (название, обозначение).

Основные элементы структуры слоёв:

• Каталог (слой, группа)
• Обновляемый каталог (слой, группа со ссылкой на файл-источник объектов слоя)
• Точечный объект
• Линейный объект
• Многоугольник

Вся структура и объекты дополнительных слоёв хранятся одним файлом в дополнительном каталоге программы.

Создание объектов и слоёв

Перейдите к справочнику «Дополнительные слои».

Каталог

Каталог может хранить как подкаталоги, так и точечные, линейные объекты и многоугольники одновременно.

При соответствующих настройках объектам внутри каталога могут быть присвоены свойства того каталога, в котором они находятся. Однако, для каждого объекта в каталоге свойства могут быть изменены и являться индивидуальными.

Обновляемый каталог

Обновляемый каталог имеет ссылку на ранее созданный KML или KMZ файл (объект), содержимое которого предположительно будет меняться (может быть указана ссылка на объект в интернете). Удобно, если этот объект используется несколькими пользователями и для этого не требуется каждый раз отдельно загружать необходимый файл, достаточно просто задать его расположение и период обновления в расширенных настройках каталога во вкладке «Обновление»:

Точечный объект

Для создания точечного объекта укажите щелчком на карте его место и нажмите кнопку «Сохранить» в окне «Свойства точечного объекта».

Линейный объект

Чтобы построить линейный объект на карте, укажите одиночными щелчками точки, между которыми будет строиться прямая линия. Построение выполняется от активной точки, размер которой больше относительно других точек на линии. Активной может являться любая точка на линии. После построения линии нажмите кнопку «Сохранить» в свойствах объекта. Также построение линейного объекта возможно при зажатой левой кнопки мыши. В этом случае первая точка выставляется как от одиночного нажатия.

В результате происходит соединение предыдущей и текущей точки прямой линией. Для удаления последней точки при построении линейного объекта нажмите «Esc» на клавиатуре.

Площадной объект (многоугольник)

Принцип построения многоугольника не отличается от построения линейного объекта, разница лишь в том, что при создании многоугольника происходит закрашивание области между синей и активной точками многоугольника.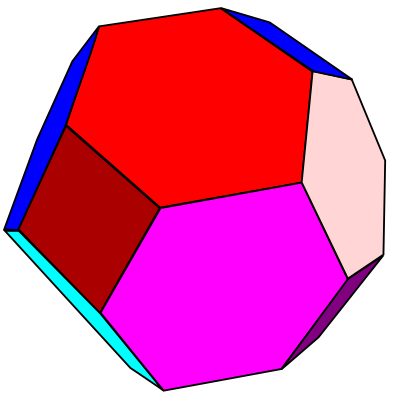

Для удаления последней отмеченной точки при построении многоугольника нажмите «Esc» на клавиатуре.

Редактирование объектов и слоев

Редактирование объектов и слоев на карте возможно только когда открыто окно свойств (при создании и редактировании свойств объекта или слоя).

Дополнительная информация

Для внесения дополнительной информации об объекте воспользуйтесь вкладкой «Описание». Текст можно вводить в HTML. Существует возможность форматирования текста и вставки изображений.

Функция управления времени

Данная функция позволяет устанавливать время отображения объекта на карте. Для этого щелкните «Указать время» во вкладке «Описание» и в открывшемся диалоговом окне укажите период отображения объекта, после чего нажмите кнопку «Установить».

В данном примере объект будет отображаться на карте с 07.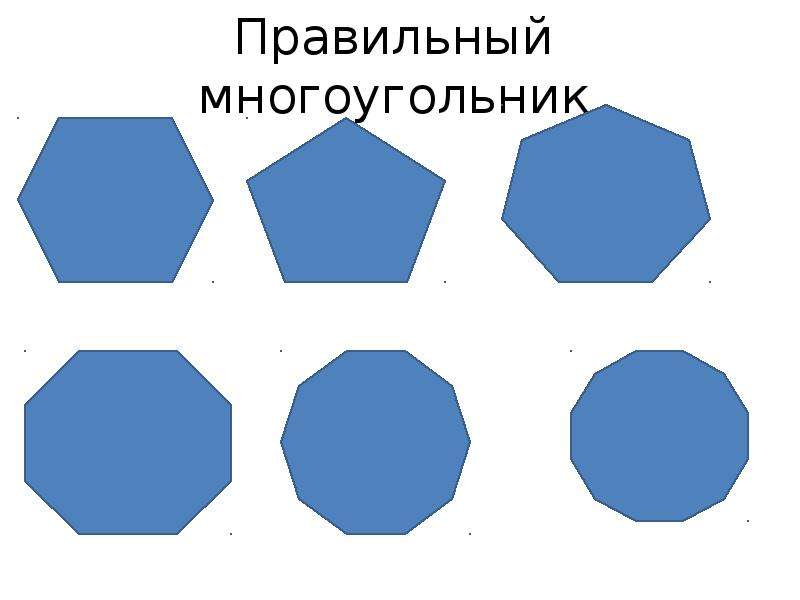 05.2011 09:00 по 08.05.2011 00:00. По истечению заданного времени отображение объекта на карте прекратится. Чтобы убрать период отображения, щелкните «Сбросить» в справочнике «Дополнительные слои» или во вкладке «Описание расширенных настроек объекта».

Также в справочнике существует возможность выбора фильтра по времени отображения объектов на карте.

Для этого нажмите в пиктограммном меню кнопку «Установить по времени» и выберите необходимый фильтр:

• фильтровать по текущему времени;
• установить свой временной интервал.

Если ни один фильтр не выбран, то на карте будут отображаться все объекты.

Стиль

Во вкладке «Стиль» можно настроить стиль отображения объекта на карте. В зависимости от редактируемого объекта доступны следующие параметры для изменения:

• иконка отображения точечного объекта на карте;
• цвет и ширина линий линейного объекта и многоугольника;
• цвет и тип заливки многоугольника;
• цвет и шрифт подписи объекта (для точечного, линейного объектов и многоугольника).

Координаты точечного объекта

В расширенных настройках во вкладке «Координаты» можно выбрать привязку точечного объекта по заданным координатам или определенному адресу на карте.

Ниже рассмотрен пример добавления изображения к точечному объекту на карте с привязкой к адресу.

Во вкладке «Координаты» указывается адрес здания, к которому необходимо привязать объект:

Во вкладке «Описание» требуется ввести относительный путь к картинке в виде кода:
<img src=»c:/pic/1.jpg»>

В результате при щелчке на объект отображается добавленная картинка в его информационной карточке:

Редактирование линейного объекта и многоугольника

Существует возможность добавления новых точек в редактируемом многоугольнике и линейном объекте. В режиме редактирования подсвечиваются все точки объекта и при щелчке в любой отрезок на линии или грань многоугольника добавляется новая точка.

Настройки

Для перехода к настройкам модуля, нажмите кнопку «Параметры» в правом верхнем углу программы и выберите пункт «Дополнительные модули». Раскройте блок «Дополнительные модули» одним щелчком мышки и нажмите кнопку «Настроить».

Соединение с интернетом

Если справочник «Дополнительные слои» содержит слои, обновляемые через интернет, то необходимо выполнить соответствующие настройки соединения с интернетом в этом блоке.

Резервная копия

• Восстановить из резервной копии: восстановление всей структуры и объектов дополнительных слоев из ранее созданной резервной копии.
• Создать резервную копию: сохранение всей структуры и объектов дополнительных слоев в отдельный kmz-файл.

Урок 14. призма — Геометрия — 10 класс

Геометрия, 10 класс

Урок № 14. Призма

Перечень вопросов, рассматриваемых в теме:

• Понятие призмы и виды призм;
• Элементы призмы: вершины, ребра, грани;
• Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
• Призма как модель реальных объектов;
• Пространственная теорема Пифагора.

Глоссарий по теме

Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

Боковые грани – все грани, кроме оснований.

Боковые ребра – общие стороны боковых граней.

Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.

Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.

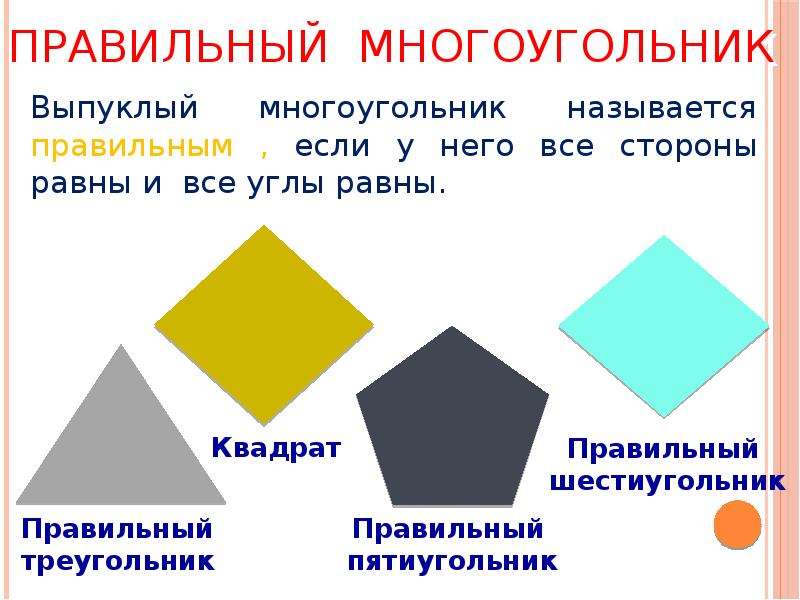
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.

Площадь полной поверхности призмы – сумма площадей всех ее граней.

Площадь боковой поверхности призмы – сумма площадей ее боковых граней.

Параллелепипед – призма, все грани которой – параллелограммы.

Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С.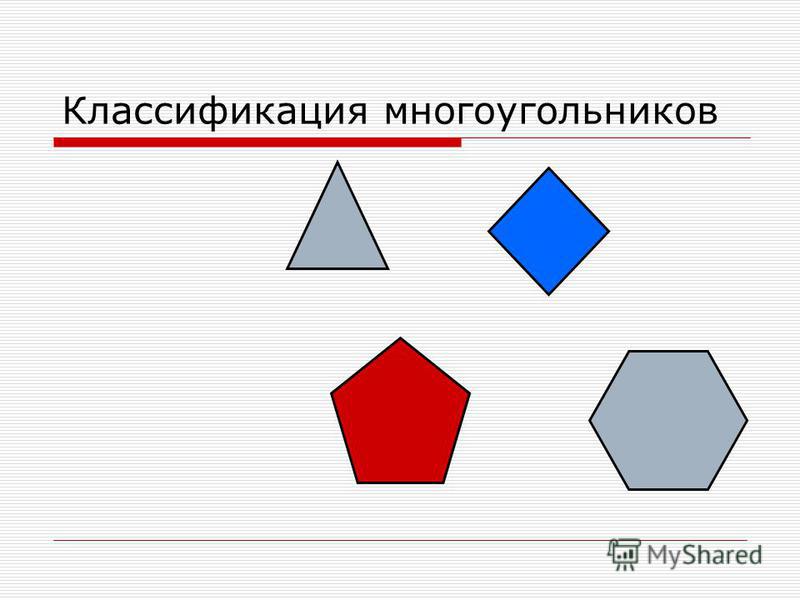 Б. и др. Математика: алгебра и начала математического анализа,

геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.

Открытые электронные ресурсы:

Открытый банк заданий ФИПИ http://ege.fipi.ru/

Теоретический материал для самостоятельного изучения

Определение призмы. Элементы призмы.

Рассмотрим два равных многоугольника А₁А₂…А_n и В₁В₂…В_n, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А₁В₁, А₂В₂…А_nВ_n, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Рисунок 1 – Призма

Заметим, что каждый из n четырехугольников (A₁A₂B₁B_2, …A_nA₁B₁B_n) является параллелограммом. Убедимся в этом на примере четырехугольника A₁A₂B₁B₂. _{A1A2 и B1B2 параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А1В1 и А2В2 по условию. Таким образом, в четырехугольнике A1A2B1B2 противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.}

Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.

На рисунке 1 основаниями призмы являются многоугольники А₁А₂. ..А_n и В₁В₂…В_n. Боковые грани – параллелограммы A₁A₂B₁B_2, …, A_nA₁B₁B_n, а боковые ребра — отрезки А₁В₁, А₂В₂, …, А_nВ_n.

Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).

Призму с основаниями А₁А₂…А_n и В₁В₂…В_n обозначают А₁А₂…А_nВ₁В₂…В_n и называют n-угольной призмой.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма

Виды призм

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.

Высота прямой призмы равна ее боковому ребру.

На рисунке 3 приведены примеры прямых призм

Рисунок 3 – Виды призм.

Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.

Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.

Площадь полной поверхности призмы. Площадь боковой поверхности призмы.

Площадью полной поверхности призмы (S_полн) называется сумма площадей всех ее граней, а площадью боковой поверхности (S_бок) призмы – сумма площадей ее боковых граней.

Таким образом, верно следующее равенство: S_полн= S_бок+2S_осн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.

Чему равна площадь боковой поверхности прямой призмы?

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Доказательство

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом S_бок=P_оснh.

Пространственная теорема Пифагора

Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.

Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

Рисунок 4 – Прямоугольный параллелепипед

Доказательство

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁ и найдем квадрат длины его диагонали А₁С.

Для этого рассмотрим треугольник А₁АС:

Ребро АА₁ перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА₁ перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА₁АС – прямоугольный.

По теореме Пифагора получаем: А₁С²=АА₁²+АС² (1).

Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС²=ВС²+АВ².

Подставив результат в (1), получим: А₁С²=АА₁²+ВС²+АВ².

Так как в основании прямоугольник, то ВС=АD.

Таким образом, А₁С²=АА₁²+АD²+АВ².

Что и требовалось доказать

Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.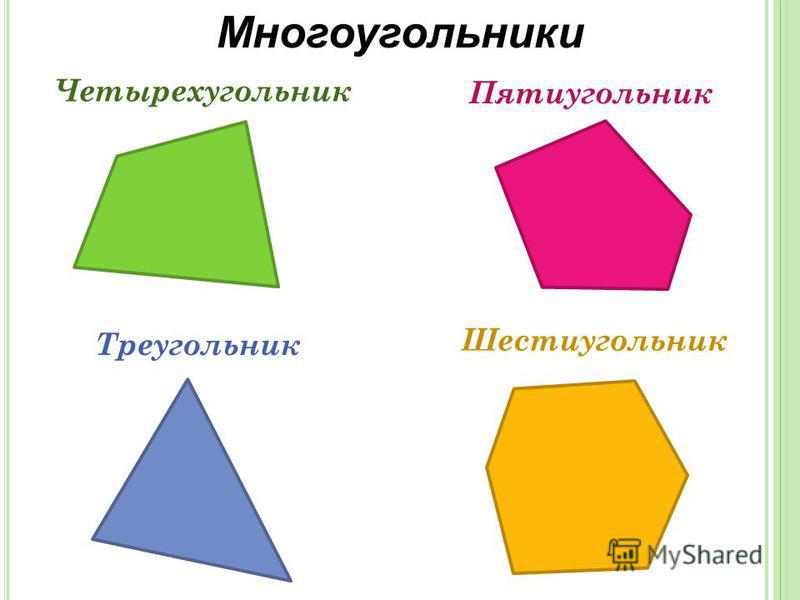

Примеры и разбор решения заданий тренировочного модуля

Задание 1.

Найдите для каждой картинки пару

1)2) 3)

4)5)

6)

Решение

Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.

Задание 2

Какие из перечисленных объектов могут быть элементами призмы?

1) параллельные плоскости

2) отрезок

3) точка

4) четырехугольник

Решение:

Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.

Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.

Ответ: 2,3,4

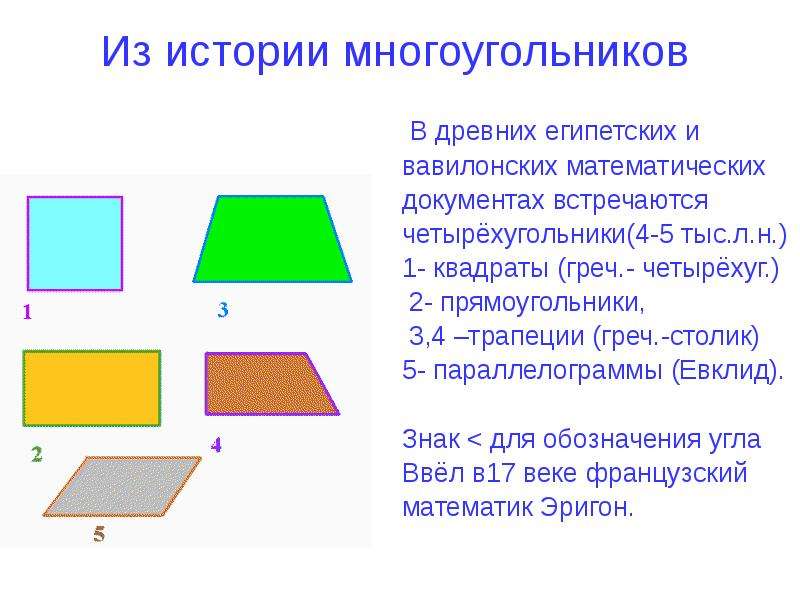
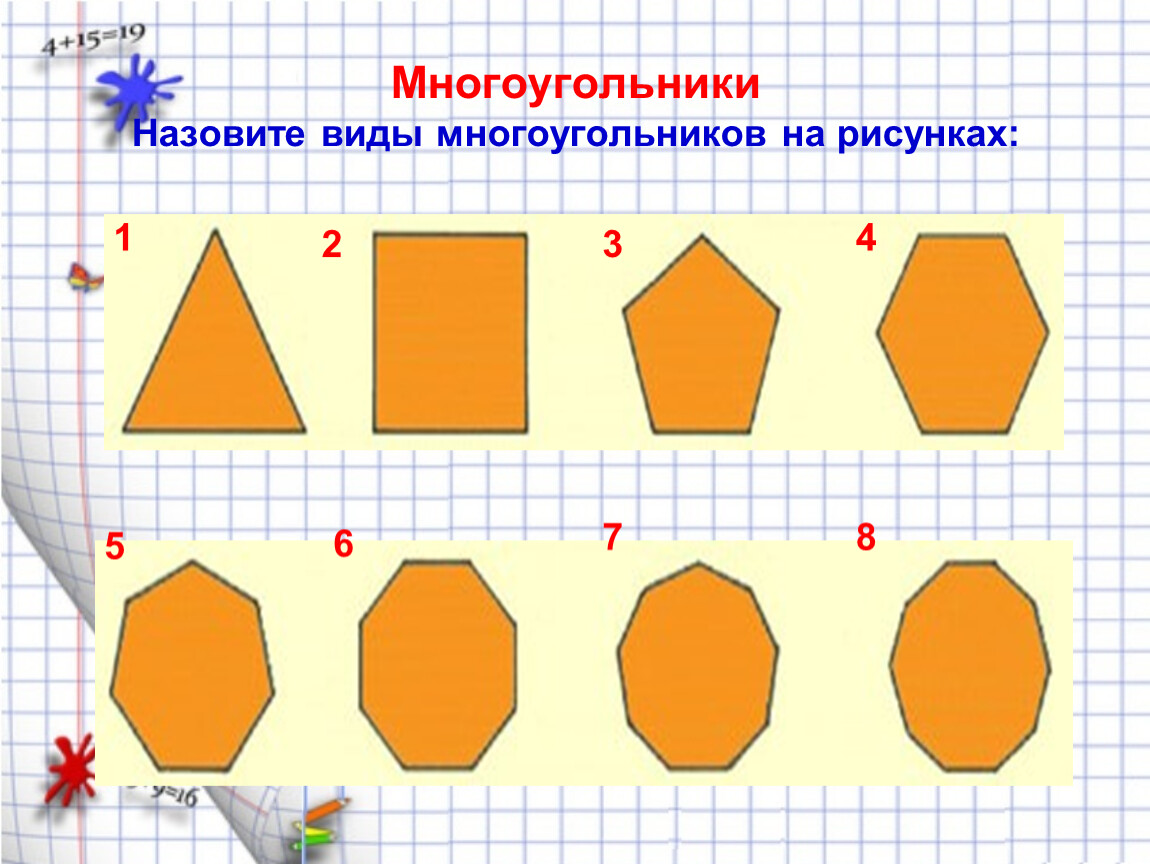
Простейшие многоугольники и их свойства — Алексей Лавриненко | Oleksiy Lavrynenko

Привет всем! В этой записи мы рассмотрели простейшую геометрическую фигуру — угол, познакомились с видами углов, и узнали об основных свойствах этой фигуры, а так же методах их обозначений. Сегодня мы узнаем, какие основные фигуры могут получиться из нескольких углов (многоугольники). И начнем, пожалуй, с треугольника.

Итак, треугольник — как следует из названия — геометрическая фигура состоящая из трех ( 🙂 ) углов (которые являются вершинами треугольника) и трех сторон:

Самой важной особенностью треугольника является тот факт, что сумма углов треугольника всегда равна 180° (пример на картинках ниже):

Как видно из картинок — сумма углов каждого из треугольников равна 180 градусам — какой бы треугольник мы не создавали.

В тексте треугольник обозначается знаком Δ и тремя заглавными латинскими буквами, которые обозначают вершины треугольника. Например, на рисунке ниже у нас имеется треугольник ABC (ΔABC) со сторонами a, b, c:

Что касается видов треугольников, то их всего три:
— прямоугольный (два угла острых (меньше 90°), и один угол прямой (равен 90°):

— остроугольный (каждый из трех углов меньше 90°):

— тупоугольный (один угол больше 90°, два других меньше 90°):

С треугольниками и их видами мы закончили. А теперь зададим себе вопрос: а что будет, если сторон и вершин у фигуры будет не три, а четыре? Начнем с квадрата. Строгое научное объяснение квадрата звучит так: квадрат — это прямоугольник, у которого все стороны равны.

А если говорить простым языком — квадрат — это фигура, у которой четыре вершины, а длина всех сторон — равная. Суть одна, а звучит, как по мне — проще, и не так сухо. Но решать — вам 🙂

В тексте квадрат обозначается заглавными латинскими буквами, обозначающими вершины квадрата. Например, на рисунке ниже у нас имеется квадрат ABCD:

Нужно отметить, что квадрат состоит из четырех углов: BAD, ABC, BCD, CDA. Что касается сторон квадрата — то они (стороны: a, b, c, d) совершенно равны:

А что будет, если в квадрате не все стороны равны? Оказывается, если в квадрате равны не все стороны, а только противоположные,а и углы равны 90° — то это будет не квадрат, а прямоугольник. Обозначается прямоугольник в тексте так же, как и квадрат — заглавными латинскими буквами. На рисунке ниже — прямоугольник ABCD (заглавные буквы обозначают вершины прямоугольника), со сторонами a, b, c, d — причем, как видно из рисунка — противоположные стороны равны друг другу: сторона a = стороне c, а сторона b = стороне d:

Ок… с прямоугольником разобрались … и перейдем к многоугольникам: геометрическим фигурам различной формы, которые, подобно треугольникам, квадратам и прямоугольникам состоят из сторон (отрезки, из которых состоит многоугольник) и вершин (точки, в которых пересекаются стороны). На рисунке ниже — многоугольник ABCDEFG (кстати, многоугольник в тексте обозначается аналогично с треугольником/квадратом/прямоугольником — заглавными латинскими буквами), состоящий из вершин и сторон a, b, c, d, e, f, g:

На этом — пока все 🙂 В следующей записи, посвященной основам геометрии мы поговорим об окружности и круге. Будет интересно!

Похожее

Как найти периметр фигур, его обозначение, измерение

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см², длина составляет 10 см. Чему равен периметр фигуры?

Как решаем:

• Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
• Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;

Ответ: 36 см.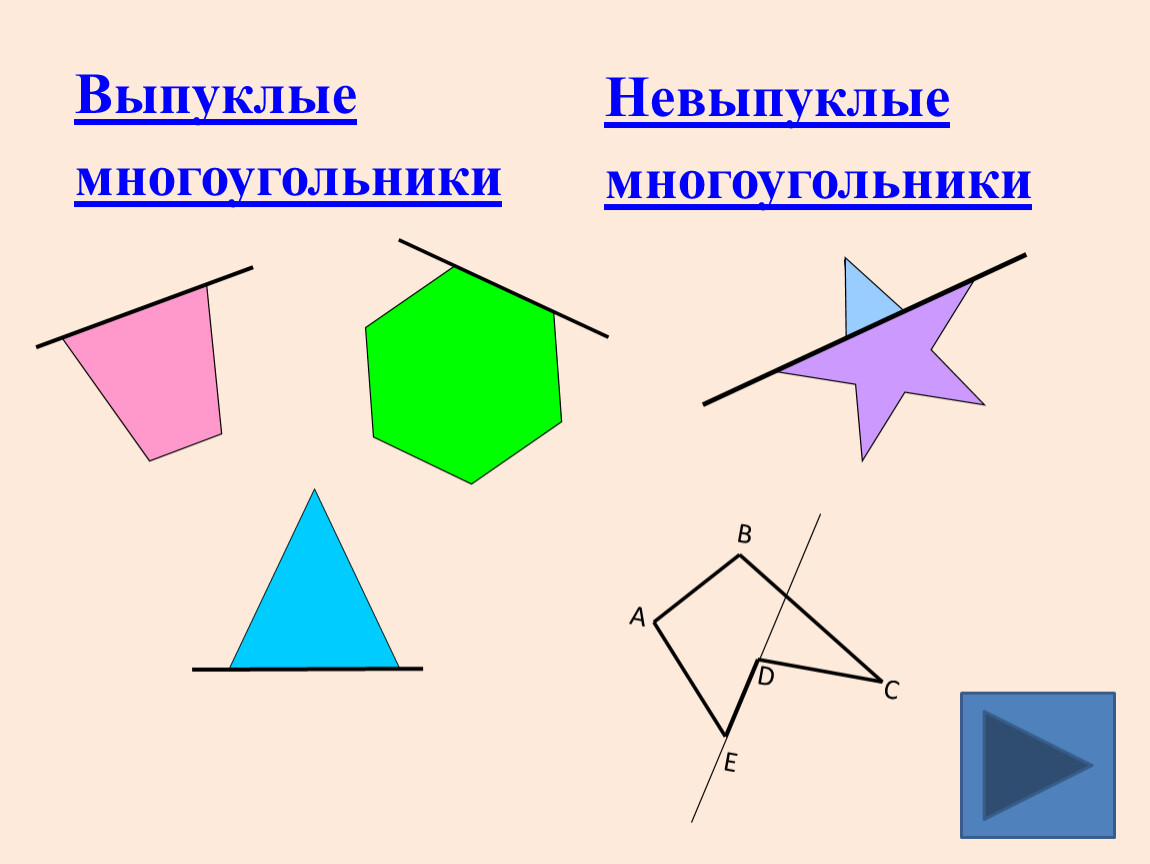

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны? 

Как решаем:

• Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Как решаем:

• Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
• Длина окружности равна π × 2 × 20 = 40π см;

Ответ: 40π см.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Описание и примеры стандартных функций SVG

Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.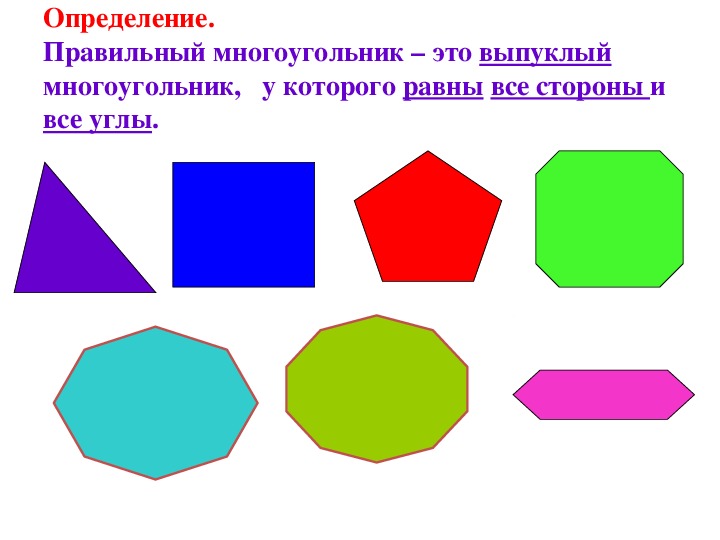
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0

Основные преимущества формата SVG.

Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW

Бесконечное полотно документа svg.

Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.

При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.

 

Взаимодействие SVG, XML с HTML, CSS, Jscript

В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.

Анимация и интерактивность SVG.

Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton.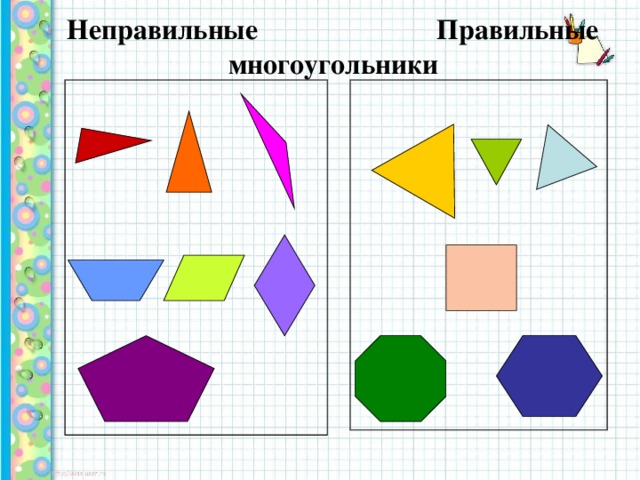 mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.

Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.js

Еще примеры анимации ⇛

Недостатки SVG формата

• С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
• Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
• В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG. Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
  Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.

 

 

UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛

Polygon Pictures — Продюсер аниме

Дверь открывается, и золотая печать разбивает звезду. Это начало 21 века. Человечество проиграло битву за планету Земля Годзилле и отправилось к звездам в поисках нового дома. Но поиски заканчиваются напрасно, заставляя их и их инопланетных союзников вернуться на Землю. Но в их отсутствие прошло 20 000 лет, и Земля стала совсем другим местом. Флора и фауна планеты теперь воплощают Годзиллу и служат ему. Земля — это планета монстров, которой правит самый большой Годзилла высотой 300 метров.Годзилла Земля. Главный герой, капитан Харуо, жаждет победить Годзиллу и вернуть планету человечеству. Там он знакомится с аборигенными потомками человеческой расы, племенем Хоутуа. Сестры-близнецы Хоутуа, Майна и Миана, приводят его к скелетным останкам Меха-Годзиллы, старого оружия против Годзиллы, которое, ко всеобщему удивлению, все еще живо в форме самогенерирующегося нанометалла. Взятые из туши Меха-Годзиллы, нанометаллы постепенно восстанавливали «Город Меха-Годзиллы», потенциальное оружие, способное уничтожить Землю Годзиллы.По мере развития стратегии между людьми и билусалудо, одной из нескольких инопланетных рас, присоединившихся к людям во время их исхода с Земли, образуется раскол. Их лидер, Галу-гу, считает, что секрет победы над Годзиллой заключается в использовании сверхчеловеческих способностей, а именно интеграции нанометаллов, но Харуо сопротивляется, опасаясь, что, побеждая монстров, они сами не должны становиться монстрами. Харуо в конечном итоге использует свои средства для победы над Землей Годзиллы, чтобы разрушить город Меха-Годзиллы, чтобы предотвратить ассимиляцию нанометаллов, убив Галу-гу.Однако его подруга детства Юко была поглощена интеграцией нанометаллов и впала в кому с мертвым мозгом. Человеческая раса, в очередной раз, потеряна. Метфис, командир жреческой инопланетной расы Экзиф, восхищается чудесным выживанием Харуо. Он начинает привлекать последователей. Exif тайно укрывала этот результат как свою «конечную цель». Миана и Майна предупреждают Метфиса, а Харуо начинает сомневаться в следующем шаге человечества. Не имея средств победить Годзиллу на Земле, человечество наблюдает, как король Гидора, облаченный в золотой свет, спускается на планету.Земля снова сотрясается, когда война переходит в более высокое измерение. Что такое Годзилла на самом деле? Есть ли у человечества шанс? Есть ли будущее в глазах Харуо? Узнайте в финале. (Источник: Официальный сайт)

полигональных изображений  | AWS Thinkbox

Компания Polygon Pictures (PPI) из Токио, основанная в 1983 году, стремится «делать то, что никто другой не делал, в непревзойденном качестве, чтобы весь мир мог видеть и наслаждаться». В дополнение к созданию анимации для фильмов, игр, выставок и других различных средств массовой информации, заслуги PPI включают отмеченный Daytime Emmy® полнометражный телесериал CG «Трансформеры Прайм» и «Звездные войны: Войны клонов», а также удостоенный премии Annie Award «Трон: Восстание».Чтобы гарантировать, что компания максимально использует вычислительные ресурсы для жестких производственных графиков, PPI использует крайний срок Thinkbox Software для управления своей фермой рендеринга.

PPI ранее использовала собственную систему, разработанную собственными силами, но в 2010 году перешла на Deadline через дистрибьютора программного обеспечения IndyZone Co., Ltd. обслуживание усложнилось, пришлось искать новое решение.Принимая во внимание его обширную поддержку приложений, высокую гибкость и расширяемость скриптов, мы выбрали Deadline», — сказал Кейичи Камеда, группа исследований и разработок Polygon Pictures.

Чтобы использовать весь потенциал внутренних ресурсов PPI, студия использует Deadline для использования около 400 рабочих станций художников (3000 ядер) для рендеринга в режиме ожидания, в дополнение к примерно 130 машинам (1500 ядер) в выделенной ферме рендеринга. Когда пользователь выходит из рабочей станции, она автоматически подключается к ферме рендеринга в качестве узла рендеринга.Благодаря настройкам приоритета Deadline PPI также может ранжировать задания по важности и соответствующим образом распределять ресурсы между несколькими проектами.

Камеда отметил, «Вначале мы управляли своей работой только по приоритету. Поскольку для одновременного выполнения нескольких проектов требовалось больше заданий, назначение приоритетов между проектами усложнилось, поэтому мы начали создавать пулы проектов и изменили порядок пулов на каждом узле. С помощью Deadline мы можем упорядочить пулы на каждом узле, еженедельно оценивая использование ресурсов для заданий, и обнаружили, что управление пулами в одном репозитории является очень эффективным способом обработки заданий.С нашими текущими настройками, если задание с более высоким приоритетом отправляется на узел рендеринга, он должен либо дождаться завершения текущих заданий, либо остановиться, чтобы начать задания с наивысшим приоритетом».

Работая в 64-разрядной версии Windows 7 с некоторыми Apple OSX, PPI настраивает монтирование дисков и приложений на основе безопасности доступа к проекту, а также настраивает существующие отправки и сценарии подключаемых модулей. Поскольку Deadline изначально поддерживает широкий спектр приложений, PPI смогла легко интегрировать его в свой конвейер.

«Помимо рендеринга из 3D-приложений, используемых нашими художниками, такими как Maya, NUKE, Houdini и 3ds Max, мы также используем Deadline для широкого спектра пакетных процессов, таких как преобразование последовательностей изображений в файлы QuickTime», —  объяснил Ацуши Тамори, Руководитель группы освещения и композитинга, Polygon Pictures.

Используя открытый API Deadline, компания PPI создала набор собственных сценариев, инструментов и настроек, а также высоко оценила простой графический интерфейс Deadline. «Контроль сроков позволяет легко понять статус рендеринга проектов, чтобы мы могли адаптироваться к меняющимся потребностям на этаже студии»,  Тамори сказал.

В настоящее время PPI работает над фильмами «Рыцари Сидонии: Битва за девятую планету» режиссера Хироюки Сэсита и «Рония, дочь разбойника» режиссера Горо Миядзаки, а также направляет свои усилия на создание нового «японского» визуального стиля. сочетая свои непревзойденные производственные ноу-хау и возможности технического развития с признанным во всем мире качеством японской анимации.

Полигон Пикчерз Инк.| Daijob: Работа в Японии! Работа в Японии!

Название компании	Полигон Пикчерз Инк.
Страна штаб-квартиры компании	Япония
Местонахождение компании	Япония
Информация о компании	Polygon Pictures, основанная в 1983 году, является одной из старейших и наиболее признанных студий цифровой анимации в мире. Наша продакшн-студия объединяет более 300 креаторов со всего мира, которые посвящают свои дни созданию ультрасовременного цифрового контента. В дополнение к полнометражным, полностью компьютерным телесериалам, таким как «Трансформеры Прайм», получившие премию «Эмми», и «Звездные войны: Войны клонов», PPI создает цифровую анимацию для фильмов, видеоигр, впечатлений от виртуальной реальности и многого другого; а в 2013 году мы создали в Малайзии совместную студию Silver Ant PPI Sdn. Bhd., чтобы еще больше увеличить наши производственные возможности.PPI также управляет лицензированием игр, которые мы финансировали и выпускали, таких как Knights of Sidonia, Ajin: Demi-Human и Pingu in the City. Сочетая наше непревзойденное производственное ноу-хау с международно признанным качеством японской анимации, PPI стремится стать ведущей компанией в сфере контента.
Промышленность	Издательство/Реклама/Печать/Вещание
Местоположение	3-20-1 Минамиазабу, Минато-ку, Токио Дайва Азабу Терраса 1F
Президент	Сиота Сюдзо
Год основания	1983
Капитал	100 000 тысяч иен ​​
Перечислен на	Н/Д
Количество сотрудников	Прибл. 300 (включая подрядчиков проекта)
Описание деятельности	Планирование, производство и лицензирование цифрового контента, такого как фильмы, телепрограммы, телевизионные рекламные ролики, выставочные видеоролики, веб-/интеллектуальные устройства, разработка персонажей
Место работы (ближайшая станция)	В 10 минутах ходьбы от выхода 4 станции Сирокане Таканава линии Намбоку и линии Тоэй Мита В 12 минутах ходьбы от выхода 1 и выхода 2 станции Хироо линии Хибия токийского метро
URL-адрес	http://www.ppi.co.jp/

Безопасность | Стеклянная дверь

Пожалуйста, подождите, пока мы проверим, что вы реальный человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, отправьте электронное письмо чтобы сообщить нам, что у вас возникли проблемы.

Veuillez терпеливейший кулон Que Nous vérifions Que Vous êtes une personne réelle. Votre contenu s’affichera bientôt. Si vous continuez à voir ce сообщение, связаться с нами по адресу Pour nous faire part du problème.

Bitte warten Sie, während wir überprüfen, dass Sie wirklich ein Mensch sind. Ихр Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, Информировать Sie uns darüber bitte по электронной почте и .

Эвен Гедульд А.У.Б. terwijl мы verifiëren u een человек согнуты. Uw содержание wordt бинненкорт вергегевен. Als u dit bericht blijft zien, stuur dan een электронная почта naar om ons te informeren по поводу ваших проблем.

Espera mientras verificamos Que eres una persona real.Tu contenido se sostrará кратко. Si continúas recibiendo este mensaje, информация о проблемах enviando электронная коррекция .

Espera mientras verificamos Que eres una persona real. Tu contenido aparecerá en краткий Si continúas viendo este mensaje, envía un correo electronico a пункт informarnos Que Tienes Problemas.

Aguarde enquanto confirmamos que você é uma pessoa de verdade. Сеу контеудо será exibido em breve. Caso continue recebendo esta mensagem, envie um e-mail para Para Nos Informar Sobre O Problema.

Attendi mentre verificiamo che sei una persona reale. Il tuo contenuto verra кратко визуализировать. Se continui a visualizzare questo message, invia удалить все сообщения по электронной почте indirizzo для информирования о проблеме.

Включите Cookies и перезагрузите страницу.

Этот процесс выполняется автоматически. Вскоре ваш браузер перенаправит вас на запрошенный вами контент.

Подождите до 5 секунд…

Перенаправление…

Код: CF-102/6cec6a48aee8359b

Polygon Pictures раскрывает полное название, подробности сюжета и визуальные эффекты предстоящего аниме «Годзилла»

Polygon Pictures представляет официальное название, детали сюжета и новейшие визуальные эффекты предстоящего аниме Годзилла .

---

Написанное Каменом Райдером Геймом, сценаристом , Геном Уробучи, грядущее аниме про Годзиллу, созданное Polygon Pictures, представило свое официальное название — Годзилла: Планета монстров или  Годзилла: Кайдзю Вакусе.

Официальный визуальный тизер отмечает следующий слоган: «Мы обязательно вернем себе эту «Планету»».

Годзилла: Планета монстров будет транслироваться на Netflix по всему миру в конце этого года.

Официальный обзор сюжета, описанный Polygon Pictures, выглядит следующим образом:

Последнее лето 20 века.В этот день люди узнают, что они не единственные правители планеты Земля.

Появление гигантских живых существ «Кайдзю» и окончательное существование, уничтожающее всех монстров: Годзилла. В битве с кайдзю, которая длилась полвека, люди терпели постоянные поражения и, наконец, планируют сбежать с Земли. А в 2048 году только те, кого выбрал А.И. управляемый центральным правительством, поднялся на борт межзвездного эмигрантского космического корабля «Аратрум», чтобы направиться к «Тау Цетус е», планете за пределами 11. 9 световых лет. Однако различия в условиях окружающей среды между Землей и Тау е, к которым они наконец прибыли через 20 лет, намного превышали предсказанные цифры и не считались средой, пригодной для жизни людьми.

Молодой человек на эмигрантском корабле: Харуо, увидевший своих родителей, убитых Годзиллой на его глазах, когда ему было 4 года, 20 лет думал только об одном: вернуться на Землю и победить Годзиллу. Исключенная из возможности эмиграции, поскольку условия жизни на корабле ухудшаются, группа «Возвращенцев с Земли» во главе с Харуо стала большинством и решает вернуться на Землю через опасную дальнюю гиперпространственную навигацию.Однако Земля, которую они вернули, уже прошла возраст в 20 000 лет и стала неизвестным миром с экосистемой, в которой правит Годзилла.

В конце концов, люди вернут себе Землю? И что увидит Харуо помимо своей судьбы?

В главных ролях озвучивают Юки Кадзи, Такахиро Сакураи, Мамору Мияно, Дзюнъити Сувабе, Кана Ханадзава и Томокадзу Сугита.

Кроме того, Кобун Сидзуно ( Детектив Конан: Самый мрачный кошмар, Кулак Полярной звезды: Легенда о Кенширо ) и Хироюки Сешита ( Аджин, Рыцари Сидонии ) указаны в качестве режиссеров аниме.

ОБНОВЛЕНИЕ 28 марта 2017 г.: Сеть новостей аниме сообщила, что этот проект будет кинотрилогией.

Источники: Polygon Pictures и Anime News Network

Anime Studio Polygon Pictures объединяется с Game Dev Historia

Если волнение и любовь к 3DCG-адаптации Land of the Lustrous от Studio Orange — это что-то стоящее, то поклонники аниме, похоже, еще больше подогрелись к идее полностью Производство аниме 3DCG.В мире таких медиа Polygon Pictures — еще одна студия, которая некоторое время участвовала в игре 3DCG, с гордостью поддерживая проекты, включая эксклюзивные для Netflix Knights of Sidonia, и даже GODZILLA: Planet of the Monsters.

Когда создатели игр приступают к разработке 3D-игр, им доступен ряд готовых движков, упрощающих создание и реализацию 3D-моделей и фонов. Одним из самых популярных движков на сегодняшний день является «Unreal Engine 4» от Epic Game, который популярен среди игровых студий Японии и остального мира.Конечно же, должно же быть какое-то пространство для совместного использования этих активов в большом количестве работ, верно? Так считают и Polygon Pictures, и Historia Inc., специалист по разработке игр на Unreal Engine.

Ссылаясь на тот факт, что трехмерная компьютерная графика используется во многих различных формах медиа, включая аниме и игры, обе компании объявили о создании совместного предприятия под названием Elementfactory Inc.

В настоящее время это обычная практика для один и тот же контент будет совместно представлен в разных жанрах, от фильмов и телевидения до игр, виртуальной реальности и мероприятий.Кроме того, технологии производства игр и видео используются в областях, выходящих за рамки индустрии развлечений, таких как образование и архитектура. Опираясь на ноу-хау в области производства игр и компьютерной графики, разработанное двумя компаниями-инвесторами, Elementfactory, Inc. возьмет на себя роль производства и разработки 3D-моделей компьютерной графики, которые обеспечивают эффективное повторное использование на нескольких носителях. В частности, компания будет разрабатывать 3D компьютерные модели следующего поколения, в которых используется всемирно используемый движок разработки игр Unreal Engine в различных формах.

Это, безусловно, интересная идея. Возьмем в качестве примера последнюю версию Polygon Picture, Fist of the Blue Sky REGENESIS, .

В дополнение к аниме, что, если сопутствующие игры и даже виртуальная реальность могут создаваться одновременно по щелчку пальцев? Будут ли все проекты содержать одни и те же спецификации, что затруднит их различение? Будут ли модели персонажей просто экспортироваться для использования в играх, чтобы разработчикам не приходилось кропотливо перестраивать свои собственные модели? Я думаю, что возможности сотрудничества на этом уровне безграничны, и если кто-то обладает опытом и готов заставить его работать, и Polygon Pictures, и Historia кажутся безопасными ставками.

Желаем удачи Elementfactory — нам не терпится увидеть, что вы принесете к столу!

Изображения: Polygon Pictures

Polygon Pictures Профиль компании: Приобретение и инвесторы

Обзор полигональных изображений

Обновите этот профиль

• Статус
• Приобретено/​Объединено

Polygon Pictures Общая информация

Описание

Оператор студии цифровой анимации в Токио, Япония.Компания производит передовой цифровой контент для телесериалов, фильмов, видеоигр и виртуальной реальности (VR), а также управляет лицензированием названий, предоставляя качественный контент по всему миру.

Контактная информация

Хотите покопаться в этом профиле?

Мы поможем вам найти то, что вам нужно

Выучить больше

Polygon Pictures Оценка и финансирование

Тип сделки	Дата	Сумма	Оценка/ EBITDA	Пост-Вал	Статус	Долг

Эта информация доступна на платформе PitchBook. Чтобы просмотреть полный профиль Polygon Pictures, запросите доступ.

Запросить бесплатную пробную версию

Группа руководителей Polygon Pictures (6)

Обновите этот профиль

Имя	Титул	Сиденье за ​​столом	Контактная информация
Судзо Сиота	Президент и главный исполнительный директор
Ёичи Атака	Главный операционный директор
Тору Ямамори	Технический директор
Хидэки Мория	Директор по развитию бизнеса
Хирош Шимада	Член правления и вице-президент отдела анимации

Вы просматриваете 5 из 6 членов исполнительной команды.Получить полный список »

Многоугольные изображения Сигналы

Скорость роста

0,80% Еженедельный рост

Еженедельный рост 0,80%, 93-й процент

-35,5%. 530%

Несколько размеров

219x медиана

Размер Несколько 219x, 100% ile

0,00x 0,95х. 413Kx

Ключевые точки данных

подписчиков в Твиттере

5.5к

Уникальных посетителей Similarweb

15.0К

Ссылающиеся домены Majestic

314

Нефинансовые показатели PitchBook помогут вам оценить успех и рост компании с помощью присутствия в Интернете и социального охвата.

Запросить бесплатную пробную версию

Polygon Pictures Бывшие инвесторы

Имя инвестора	Тип инвестора	Холдинг	Инвестор с	Раунды с участием	Контактная информация

Эта информация доступна на платформе PitchBook.Чтобы просмотреть полный профиль Polygon Pictures, запросите доступ.

Запросить бесплатную пробную версию .