Линии графика: Линия в графике
Графика: о чем расскажет линия?
Фев 16, 2016
in Полезные статьи по рисованию by Марина ТрушниковаГрафика: о чем расскажет линия?
Знаете ли вы, как вас можно “прочитать” по рисунку? Если нет, прочтите внимательно это статью!
Перефразируя известное высказывание, хочется спросить – любите ли вы графику так, как люблю её я?
Зачаровывает ли вас утонченная изысканность линий? Восхищает ли игра черных и белых пятен? А сеточка тончайших штрихов? А чудо возникновения образа двумя-тремя касаниями карандаша?
Надеюсь, что да. Ведь черно-белое изображение – это действительно волшебство, к которому мы настолько привыкли, что не ценим его по достоинству!
“Листопад”, Марина Трушникова
А ведь если задуматься, что есть графика?
Это совершенно особый мир, созданный художником на листе бумаги, который имеет мало общего с реальной жизнью.
Он берет у реальности только часть. Но тем не менее, мы воспринимаем этот мир как понятный и существующий!
Насколько было бы забавно, если бы вокруг нас действительно ходили только черно-белые люди!
Да еще и без плоти – только с проволочным каркасом линий! Как в графических листах. Представляете? 🙂
Графика – это чудо совершенно иного мира, который мы воспринимаем реальным!
Мы свободно домысливаем недостающие качества цвета, формы, объема. И художник, и зритель в этом случае являются Творцами!
Графика – это не фотография, где посмотрел и узнал то, что увидел.
Графика – это условность, которая заставляет работать наше воображение.
Это картинка, которая вновь создает новый мир!
Конечно, степень отхода от реальности в может быть разной.
Смотрите, я покажу вам это на примере еще нескольких своих работ.
Изображение упрощается, теряет сначала объем, затем глубину, а в конце концов и реалистичность силуэта.
Но тем не менее, вы ведь понимаете, о чем рассказывает та или иная картинка?
Эта серия лаконичных изображений называется “Возрождение”. Узнаете ли вы в этих незамысловатых линиях людей? Можете ли понять мой замысел, о чем эта история? 🙂
Правда удивительно, как много может выразить одна, всего лишь одна линия?
Галерея графики Марины Трушниковой: Черно-белые сказки о жизни и любви
Это свойство человека домысливать зрительный образ просто поразительно! И именно на нем зиждется изобразительное искусство.
Каждая линия — отпечаток нашей личности!
Линия сама по себе может рассказать внимательному зрителю о многом. О характере, настроении, состоянии человека, который ее нарисовал.
Каждая линия – отпечаток нашей личности! Знаете ведь, что по нашему почерку графолог может достоверно описать человека. Так же и любая другая линия.
Вот смотрите. Я провела три линии одним карандашом с разной скоростью и силой нажима.
Определите, какая линия медленная, какая быстрая, какая проведена легко, а какая — с нажимом?
Думаю, вопрос не поставил вас в тупик?
- Первая линия проведена быстро. Видите, какой у нее тонкий летящий хвостик? Кроме того, она очень ровная – рука на скорости не успевает дрогнуть.
- Вторая линия светлее остальных. Это значит, что сила нажима на нее была меньше.
- Ну а третья – самая медленная, с нажимом. Это видно по неровности линии, и по ее неоднородности – если карандаш очень мягкий, то по краям такой линии видны крошки грифеля.
Таким образом, лишь по одной линии можно судить о настроении художника или его темпераменте, не так ли?
Давайте посмотрим несколько работ разных художников!
Это Рембрандт.
Какая динамичная линия! Какое множество штрихов! Уверенно и быстро они “лепят” объемную форму.
А это портрет матери работы Альбрехта Дюрера. Он прославился своими гравюрами.
Не правда ли, очень спокойная, отточенная линия?
Работа гравера и требует усидчивости – линию, нанесенную резцом на металл, не исправишь.
Здесь нужно быть уверенным в каждом движении!
И хоть этот портрет выполнен углем, но характер линий отражает привычно внимательное отношение художника к изображению.
Еще один портрет.
Это Николай Фешин, великолепный живописец, портретист начала 20 века.
Его линия какая-то невесомая, утонченная, очень романтичная.
Встречи в Periscope: Как создавать эскиз для картины. Трюк, подсмотренный на выставке Фешина
И еще один художник, которого не могу обойти своим вниманием. Потому что линия у него просто виртуозная!
Динамичная, одним движением формирующая силуэт и образ.
Это рисунок Валентина Серова.
Сравнивая работы разных авторов, мы хорошо видим различия в стиле их рисунка, темперамент автора и характер.
Думаю, теперь вы иначе взглянете не только на графические работы художников, но и на те рисунки и “почеркушки”, которые делаете сами, которые видите у своих близких.
Итак, линия может нам рассказать о силе нажима на карандаш и скорости движения руки. А это значит – о темпераменте и мастерстве художника, его настроении и внутреннем состоянии души.
Просто нужно быть внимательным зрителем…
Если мои размышления были вам интересны, поделитесь этой статьей в своих соцсетях!
Любите карандашные рисунки и графику?
Познакомьтесь с моей авторской техникой создания удивительных рисунков
в курсе “КАРАНДАШНЫЕ ФАНТАЗИИ”
Если вы считаете, что у вас бедное воображение, попробуйте эту методику рисования и результат вас приятно удивит!
ПОДРОБНЕЕ О КУРСЕ
Линия тренда в Excel. На разных графиках
Существует множество сфер, где может использоваться трендовая линия. Но наиболее популярной из них, безусловно, являются финансовые рынки. В бизнесе тоже она применяется довольно часто для составления отчетов и прогнозирования возможных перспектив развития проекта или компании в целом.
Также она будет полезным инструментом в тех областях человеческой деятельности, где можно составлять прогнозы, ориентируясь на статистические данные. А таких сфер значительно больше, чем может показаться на первый взгляд. В частности, к ним относятся социология, психология, программирование (использование математических моделей позволяет автоматизировать процесс прогнозирования) и так далее. Особенно это полезно в сочетании с качественным анализом информации.
Основная проблема почти любого графика с большим количеством информации в том, что в нем показания очень вариативны. Поэтому возможно появление большого количества данных, которые мешают понять, какая действительно тенденция наблюдается в этой отрасли.
Трендовая линия – это классический статистический инструмент, позволяющий без особого опыта предсказать, в каком направлении будет двигаться целевой показатель через некоторое время и в какой точке будет. Также он дает возможность косвенно определить факторы, которые влияют на образование данного тренда.
Как добавить линию тренда на график Excel
Трендовая линия дает возможность понять действующие тенденции определенного показателя. И поскольку особенно часто сей инструмент сейчас используется на финансовых рынках, то мы будем приводить на этом примере.
Трендовая линия на финансовых рынках является классическим инструментом анализа динамики котировок, которая используется еще с момента создания первой фондовой биржи. Но одной ее недостаточно, и сейчас разрабатываются все более новые технические индикаторы, которые позволяют значительно улучшить качество прогнозов. Существует еще отдельная категория индикаторов, которая позволяет непосредственно предвидеть разворот тенденции. В то же время трендовая линия дает возможность лишь констатировать имеющееся направление цены.
Поэтому рекомендуется использовать трендовую линию совместно с осцилляторами. Это категория технических индикаторов, которая успевает заметить изменение тренда до того, как это сделает трендовая линия.
Это категория технических индикаторов, которая успевает заметить изменение тренда до того, как это сделает трендовая линия.
Создание трендовой линии возможно стандартными средствами Excel. Она еще до сих пор активно используется, поэтому уметь ее строить надо. Давайте разберемся, как это сделать.
Процесс построения графика
Чтобы процесс построения трендовой линии был успешным, график должен соответствовать математической функции. Чтобы создать график, необходимо следовать этому алгоритму:
- Выделить интересующий набор ячеек.
- Зайти на панель инструментов (или, как нередко говорится, ленту) на вкладку «Главная», и там найти кнопку «Диаграммы».
- Затем нужно выбрать «Точечная, а затем «Точечная с гладкими линиями и маркерами».
После того, как пользователь сделает клик по графику, он сможет воспользоваться еще одной панелью, через которую и осуществляется добавление линии тренда на график.
Создание линии тренда
Итак, давайте перейдем на панель «Работа с диаграммами». Там находится вкладка «Макет», через которую и осуществляется добавление линии тренда на график. После того, как мы нажмем одноименную кнопку, появится возможность выбрать способ приближения. Нужно выбрать линейный тип. Затем появится черная линия, которая будет выражать действующую тенденцию.
Там находится вкладка «Макет», через которую и осуществляется добавление линии тренда на график. После того, как мы нажмем одноименную кнопку, появится возможность выбрать способ приближения. Нужно выбрать линейный тип. Затем появится черная линия, которая будет выражать действующую тенденцию.
Важно понимать, что некоторые типы графиков не поддерживают линию тренда. Поэтому рекомендуется использовать самые стандартные.
Все остальные разновидности графиков дают возможность добавлять линию тренда на них.
Настройка линии
Следующий этап – настройка. Сначала нужно добавить уравнение в график. Это делается путем двухкратного нажатия левой кнопкой мыши по диаграмме. Затем пользователю необходимо выбрать опцию «Показать уравнение на диаграмме».
Если на диаграмме находится больше одного графика, то нужно выбрать наиболее подходящий для прогнозирования.
Нужно запомнить следующие пункты, если нужно отрегулировать определенные параметры линии тренда:
- Чтобы назвать диаграмму, необходимо по ней сделать двойной клик мышью.
 Заголовок записывается в небольшом поле ввода. Чтобы определить местонахождение заголовка графика надо снова открыть вкладку «Работа с диаграммами», после чего выбрать «Макет» и «Название диаграммы». Всплывет перечень возможных расположений заголовка.
Заголовок записывается в небольшом поле ввода. Чтобы определить местонахождение заголовка графика надо снова открыть вкладку «Работа с диаграммами», после чего выбрать «Макет» и «Название диаграммы». Всплывет перечень возможных расположений заголовка. - В данном разделе находится настройка, позволяющая задать заголовки осей и их место на диаграмме. Важно то, что пользователь имеет право располагать название прямо по оси X или Y. Это дает возможность сделать внешний вид максимально удобным для чтения.
- Для внесения изменений сразу в линии, необходимо открыть вкладку «Макет» и там перейти по пунктам «Анализ – Прямая тренда». А если нажать на «Дополнительные параметры», то откроется окно, в котором можно настраивать линию тренда – регулировать ее формат, редактировать окрас, сглаживание и ряд других параметров.
- Также можно проверить трендовую линию на правдивость. Чтобы это сделать, нужно включить опцию «Разместить на график величину достоверности аппроксимации» и закрыть окно.
 Самое оптимальное значение – 1. Если наблюдаются отклонения, это говорит о степени достоверности построенной статистической модели.
Самое оптимальное значение – 1. Если наблюдаются отклонения, это говорит о степени достоверности построенной статистической модели.
Прогнозирование
Самые точные прогнозы возможны, если сделать тип графика «гистограмма». Это дает возможность сопоставить уравнения. Чтобы это сделать, надо следовать такому алгоритму:
- Открыть контекстное меню. В этом перечне нажать по пункту «Изменить тип диаграммы».
- Откроется окно настроек. Там выбирается тип «Гистограмма», а далее выбираем разновидность.
Теперь пользователь может видеть оба графика. Они содержат одну и ту же информацию, но дают возможность составлять более точные прогнозы, поскольку каждый тип графика использует свое уравнение для построения трендовой линии.
Далее перед нами стоит задача сопоставить разные диаграммы. Чтобы это сделать, надо включить визуальное отображение. Для этого выполняются следующие шаги:
- Формат гистограммы меняется на простой точечный график, какой мы делали ранее.
 Чтобы это сделать, нужно воспользоваться пунктом «Изменить тип диаграммы».
Чтобы это сделать, нужно воспользоваться пунктом «Изменить тип диаграммы». - Нажать два раза по линии тренда изменить параметры прогноза на 12 и сохранить внесенные правки.
С помощью таких параметров можно заметить, что угол наклона линии тренда отличается в зависимости от используемого графика, но все равно направление не меняется. Из этого можно сделать вывод, что недостаточно использовать лишь одну линию тренда, чтобы составлять надежные прогнозы на финансовых рынках.
Если речь идет о торговле на финансовых рынках, то использования технических индикаторов (коим трендовая линия и является) недостаточно. Нужно еще понимать фундаментальные законы экономики и общие качественные тенденции развития отрасли. Иначе даже при высоком коэффициенте достоверности реальная точность составляемых прогнозов будет очень страдать.
Уравнение линии тренда в Excel
Только лишь добавить линию тренда недостаточно, нужно еще уметь выбирать правильное уравнение, чтобы данные отображались максимально корректно. Определить, какое из них правильное, можно, ориентируясь на число достоверности. Если величина отличается от единицы, то диаграмма была настроена неверно. Соответственно, нужно по-другому отобразить график или использовать другие уравнения для расчета.
Определить, какое из них правильное, можно, ориентируясь на число достоверности. Если величина отличается от единицы, то диаграмма была настроена неверно. Соответственно, нужно по-другому отобразить график или использовать другие уравнения для расчета.
Линейная аппроксимация
Давайте приведем такой кейс: сотрудник заключал сделки в течение десяти месяцев, и каждый месяц им было совершено определенное их количество.
Построение диаграммы будет осуществляться с опорой на эти данные. Нужно просто выполнить некоторые действия, а именно:
- Добавление линии тренда на диаграмму.
- Добавление к диаграмме уравнения, которое используется для анализа тенденции и величины достоверности. Оба эти значения играют огромную роль в прогнозировании динамики любых показателей.
Предположим, у нас есть график, где введены данные и выбран тот тип отображения графика, при котором достоверность равна 0,9929, а исходя из данных диаграммы, можно сделать вывод, что сотрудник работает больше, чем до того. В таком случае с помощью графика можно определить, сколько сделок ожидается совершить в будущем. Чтобы это сделать, нужно в используемую формулу вставить номер периода.
В таком случае с помощью графика можно определить, сколько сделок ожидается совершить в будущем. Чтобы это сделать, нужно в используемую формулу вставить номер периода.
Экспоненциальная линия тренда
Этот тип линии тренда знаком сейчас многим. По этому сценарию развиваются все пандемии, а также ряд других процессов. Характерная особенность этого вида линии тренда – цифры постоянно возрастают в геометрической прогрессии. Например, 1,2,4,8 и так далее. По похожему сценарию как раз и развиваются эпидемии, поскольку чем больше больных, тем большему количеству людей может передаться заболевание.
Мы попробуем абстрагироваться от неприятных вещей и перейдем на другие сферы, например, бизнес.
Допустим, вы являетесь менеджерами, которым надо проанализировать, сколько энергии было отпущено за определенный период. Использоваться будут условные значения, которые могут расходиться с действительностью. Просто для демонстрации примера.
1Теперь, основываясь на этих данных, выполняем построение графика. Далее добавляем экспоненциальную линию тренда.
Далее добавляем экспоненциальную линию тренда.
Достоверность линии тренда в рассматриваемом нами примере составляет 0,938, что говорит, что вероятность ошибки довольно низкая. Следовательно, прогнозам можно доверять.
Логарифмическая линия тренда
Она применяется в ситуациях, когда показатели могут резко меняться. Например, сперва наблюдается стремительный рост, после чего наступает период стабильности. С помощью логарифмической линии тренда можно попытаться предсказать, насколько удачными будут продажи товара, который только появился.
Сперва компании нужно привлекать новых клиентов. Поэтому рост будет стремительный. Дальше опора идет в первую очередь на то, чтобы сделать лояльными к себе тех, кого уже удалось привлечь. Следовательно, точка приложения усилий меняется и соответственно, корректируется прирост клиентской базы.
Давайте сделаем к этому примеру такой график.
3В этом случае также ошибка аппроксимации минимальная, поэтому полученным сведениям можно доверять. Теперь давайте попробуем предположить, насколько интенсивными будут продажи в будущем. Чтобы это сделать, необходимо подставить номер соответствующего периода в качестве значения переменной x.
Теперь давайте попробуем предположить, насколько интенсивными будут продажи в будущем. Чтобы это сделать, необходимо подставить номер соответствующего периода в качестве значения переменной x.
Как вариант, возможна следующая таблица с прогнозами.
4В нашем кейсе для того, чтобы приблизительно понять, как в будущем будет реализовываться продукция, была применена такая формула: =272,14*LN(B 18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Эксель
Эта линия тренда характерна для волатильных (изменчивых) показателей. Очень хорошо его использовать для торговли криптовалютами или другими высоко рисковыми активами.
Для линии тренда этого типа характерно то увеличение, то уменьшение показателей в достаточно широком диапазоне. Его использование возможно в том числе и для обработки огромных массивов информации количественного типа. Особенно эта линия тренда часто используется при наличии большого количества экстремумов на графике (то есть, минимумов и максимумов).
График цены на нефть является наиболее удобным способом демонстрации того, как работает эта модель. Чтобы величина достоверности была близкой к единице, пришлось выставить шестую степень. Но такая линия тренда дает возможность составлять достаточно верные прогнозы.
5Выводы
Построение линии тренда – это довольно простая процедура. А вот анализ данных с ее использованием – уже задачка посложнее. Но с помощью встроенных средств Excel можно составлять эффективные прогнозы развития самых разных показателей из разных сфер. И хотя использование трендовой линии по большей части автоматизировано в современных программах, иногда может потребоваться использование Excel для этой цели.
Вообще, для составления эффективных прогнозов одной трендовой линии недостаточно. Это не панацея, и не стоит надеяться, что настолько элементарная математическая модель способна творить чудеса. Тем не менее, это один из самых простых элементов статистического анализа. И теперь вы знаете, как его использовать в реальной работе.
Оцените качество статьи. Нам важно ваше мнение:
Как в Excel добавить к диаграмме линию тренда или линию скользящего среднего
Глядя на только что созданную диаграмму в Excel не всегда легко сразу понять тенденцию развития данных. Некоторые диаграммы состоят из тысяч точек данных. Иногда можно на глаз определить, в каком направлении изменяются данные со временем, в других случаях потребуется прибегнуть к некоторым инструментам Excel, чтобы определить, что же происходит. Сделать это можно при помощи линии тренда и линии скользящего среднего. Чаще всего для того, чтобы определить, в каком направлении происходит развитие данных, в диаграмме используется линия тренда. Чтобы автоматически рассчитать такую линию и добавить её к диаграмме Excel, нужно сделать следующие шаги:
- В Excel 2013 кликните в любом месте диаграммы и затем нажмите иконку с символом плюс (+) рядом с диаграммой, чтобы открыть меню Элементы диаграммы (Chart elements).
 Другой вариант: нажмите кнопку Добавить элемент диаграммы (Add Chart Elements), которая находится в разделе Макеты диаграмм (Chart Layouts) на вкладке Конструктор (Design).
Другой вариант: нажмите кнопку Добавить элемент диаграммы (Add Chart Elements), которая находится в разделе Макеты диаграмм (Chart Layouts) на вкладке Конструктор (Design). - Отметьте галочкой параметр Линия тренда (Trendline).
- Чтобы настроить тип линии тренда, кликните направленную вправо стрелку и выберите один из предложенных вариантов (линейная, экспоненциальная, линейный прогноз, скользящее среднее и т.д.).
Чаще всего используются обычный линейный тренд и линия скользящего среднего. Линейный тренд – это прямая линия, расположенная таким образом, чтобы расстояние от неё до любой из точек графика было минимальным. Эта линия полезна в том случае, если есть уверенность, что последующие данные будут соответствовать тому же шаблону.
Очень полезна линия скользящего среднего по нескольким точкам. Такая линия, в отличие от линейного тренда, показывает усреднённую тенденцию по заданному числу точек на графике, которое можно изменить. Линию скользящего среднего используют, если формула, предоставляющая данные для построения графика, изменяется со временем, и тренд должен быть построен только по нескольким предшествующим точкам. Чтобы построить такую линию, выполните шаги 1 и 2 из описанных выше, а затем сделайте вот что:
Линию скользящего среднего используют, если формула, предоставляющая данные для построения графика, изменяется со временем, и тренд должен быть построен только по нескольким предшествующим точкам. Чтобы построить такую линию, выполните шаги 1 и 2 из описанных выше, а затем сделайте вот что:
- Кликните направленную вправо стрелку в строке Линия тренда (Trendline) и выберите вариант Скользящее среднее (Moving average).
- Проделайте шаги 1 и 2 из предыдущего примера ещё раз и нажмите Дополнительные параметры (More options).
- В открывшейся панели Формат линии тренда (Format Trendline) убедитесь, что флажком отмечен вариант Линейная фильтрация (Moving Average).
- Справа от параметра Линейная фильтрация (Moving Average) находится поле Точки (Period). Здесь задаётся количество точек, которое нужно использовать для вычисления средних значений для построения линии тренда.
 Установите такое количество точек, которое, по Вашему мнению, будет оптимальным. Например, если Вы считаете, что определённая тенденция в данных сохраняется неизменной только для последних 4 точек, то введите число 4 в данном поле.
Установите такое количество точек, которое, по Вашему мнению, будет оптимальным. Например, если Вы считаете, что определённая тенденция в данных сохраняется неизменной только для последних 4 точек, то введите число 4 в данном поле.
Линии тренда в Excel – это отличный способ получить больше информации об имеющемся наборе данных и о том, как они изменяются со временем. Линейный тренд и скользящее среднее – два типа линий тренда, наиболее распространённых и полезных для бизнеса.
Оцените качество статьи. Нам важно ваше мнение:
Линии на графике не появляются
Я пытаюсь plot следующую функцию в MATLAB, но строки не отображаются. Может ли кто-нибудь помочь мне с этим, пожалуйста. Спасибо.
x=1;
PiD=10;
PiC=20;
PiP=50;
Vhigh=4;
Vlow=0;
Vmax=5;
Vmin=-1;
A1=2;
A0=-4;
Dt=[(Vmax/A1)-(Vmax/A0)]+[((Vlow-Vmin)+(Vmax-Vhigh))/A1]+[((Vmax-Vhigh)+(Vlow-Vmin))/A0];
for i=-x:0.1:x
DPiI=PiD+[PiC*(Vhigh/A1)]+PiP*i+PiC*i;
PiE=DPiI/Dt;
end
plot (x,PiE)
Поделиться Источник Hamza Mezo 16 августа 2018 в 20:59
2 ответа
- Crystal reports строк не отображаются
У меня есть отчет crystal для счета-фактуры, который отформатирован с некоторыми горизонтальными и вертикальными линиями.
 Вертикальные линии пересекают ряд групповых и детальных сечений. Crystal reports-это версия 13, и я использую ее в конструкторе в Visual Studio 2013. У меня две проблемы 1)…
Вертикальные линии пересекают ряд групповых и детальных сечений. Crystal reports-это версия 13, и я использую ее в конструкторе в Visual Studio 2013. У меня две проблемы 1)… - Метки не отображаются на графике
Вчера должен был обновить библиотеку highcharts. После обновления у меня возникла проблема с метками на графике. На графике появилась только одна метка (первая серия в данных). Для всего, что метки не отображаются, добавляется свойство html: visilibty=hidden. Например: jsfiddle Кто-нибудь знает,…
2
Я сделал некоторые дополнения к ответу лопитала, и он, похоже, прошел первоначальное тестирование.
...
for i=-x:0.1:x
DPiI=PiD+[PiC*(Vhigh/A1)]+PiP*i+PiC*i;
PiE(j)=DPiI/Dt;
i2(j) = i;
j=j+1;
end
plot (i2,PiE,'bo-')
Поделиться Tom 16 августа 2018 в 22:03
0
The PiE variable is a scalar. Try making it a vector as follows:
...
PiE = []
j = 1;
Dt=[(Vmax/A1)-(Vmax/A0)]+[((Vlow-Vmin)+(Vmax-Vhigh))/A1]+[((Vmax-Vhigh)+(Vlow-
Vmin))/A0];
for i=-x:0.1:x
DPiI=PiD+[PiC*(Vhigh/A1)]+PiP*i+PiC*i;
PiE(j)=DPiI/Dt;
j=j+1;
end
plot (x,PiE)
Try making it a vector as follows:
...
PiE = []
j = 1;
Dt=[(Vmax/A1)-(Vmax/A0)]+[((Vlow-Vmin)+(Vmax-Vhigh))/A1]+[((Vmax-Vhigh)+(Vlow-
Vmin))/A0];
for i=-x:0.1:x
DPiI=PiD+[PiC*(Vhigh/A1)]+PiP*i+PiC*i;
PiE(j)=DPiI/Dt;
j=j+1;
end
plot (x,PiE)
Поделиться lhopital 16 августа 2018 в 21:37
Похожие вопросы:
Данные отображаются только в виде нулей на графике
У меня есть лист excel с данными в нем: Это приводит к диаграмме, но диаграмма показывает только 0 в качестве данных: Каждая моя клетка-это формула. Я попытался записать значение в ячейку, и оно…
Интервальная роль i-линии не отображаются в линейном графике Google
Я пытаюсь добавить минимальные и максимальные ограничения в диаграмму Google, которую я генерирую с помощью скрипта Perl из данных CSV — используя роль интервала для этих 2 значений. К сожалению,…
Прикрепление Textbox к точке или линии на графике в Excel/VBA
Мне было интересно, как прикрепить textbox к точке или линии на диаграмме Excel для макроса, над которым я работаю. Я использую метод .AddTextbox , такой как…
Я использую метод .AddTextbox , такой как…
Crystal reports строк не отображаются
У меня есть отчет crystal для счета-фактуры, который отформатирован с некоторыми горизонтальными и вертикальными линиями. Вертикальные линии пересекают ряд групповых и детальных сечений. Crystal…
Метки не отображаются на графике
Вчера должен был обновить библиотеку highcharts. После обновления у меня возникла проблема с метками на графике. На графике появилась только одна метка (первая серия в данных). Для всего, что метки…
Линии не отображаются на графике Matplotlib
Я пытаюсь построить три линии на одном и том же участке в Matplotlib. Это InvoicesThisYear, DisputesThisYear и PercentThisYear (то есть Disputes/Invoices) Исходные входные данные представляют собой…
Строки Div в FusionChart XT не работают в IE11
Я пытаюсь отобразить два графика с FusionChartXT, но линии div не отображаются на втором графике в IE. Первый график всегда выглядит правильно, а на другом графике линии div исчезают. Это часть…
Первый график всегда выглядит правильно, а на другом графике линии div исчезают. Это часть…
Почему метки не отображаются на графике?
Я работаю над проектом с Angular 4 и AmCharts. Мне нужно отобразить простую метку на графике, в левом верхнем углу. Мой конфигурационный код для диаграммы выглядит следующим образом: this.chart =…
Линии сетки не отображаются на моем графике в блокноте Jupter
я пытаюсь построить график распределения с помощью seaborn, но не получаю линий сетки на графике, это просто. import seaborn as sns %matplotlib inline sns.distplot(df_0[‘temp’], bins=20) Below is…
Нет точек, отображаемых на графике
я искал способ отображения точек на этом графике
Алгоритм: понять, когда две линии графика похожи
Я пытаюсь разработать скрипт, способный понять, когда две линии графика похожи (они имеют одинаковое направление или одинаковые значения).
Например, предположим, что у меня есть два массива:
array1 = [0,1,2,3,4,5,6,7,8,9,10];
array2 = [2,3,4,5,6,7,8,8,10,11,12];
Как вы можете видеть, они оба роста и их значения очень похожи.
На данный момент я нашел идеально работающее решение, используя алгоритм DTW. Проблема в том, что DTW имеет «обучающую часть» очень быстро (я просто должен хранить много линий диаграммы), но у него есть тяжелая часть прогнозирования , потому что он сравнивает последнюю линию диаграммы со всеми остальными в памяти.
Поэтому мой вопрос таков: можно ли переместить время вычислительной сложности во время обучающей части, чтобы иметь более быстрое предсказание? Например, создание дерева поиска или что-то в этом роде? И если это возможно, то в соответствии с каким конкретным значением я могу сгруппировать информацию?
У вас есть какие-нибудь советы или полезные ссылки?
algorithm machine-learning artificial-intelligence binary-search-tree cluster-analysisПоделиться Источник Jacob 20 сентября 2017 в 08:07
2 ответа
- Нарисуйте вертикальную линию, когда две линии пересекаются в Highcharts
У меня есть график температурной линии, и я хочу нарисовать красную вертикальную линию, когда две температуры (температура поверхности и точка росы) пересекаются.
 Пока что я рисую вертикальный прямоугольник поверх своего графика в тех местах, где, по моим расчетам, он пересекается. Он работает…
Пока что я рисую вертикальный прямоугольник поверх своего графика в тех местах, где, по моим расчетам, он пересекается. Он работает… - Алгоритм поиска того, где именно две строки совпадают/отличаются
Я работаю над поиском сходства/различий в исходном коде различных программ java. Я использовал реализацию алгоритма Левенштейна, чтобы найти, насколько похожи две программы. Я хочу знать, есть ли какой-нибудь алгоритм, который может помочь найти точные позиции, где две строки отличаются.
1
Это часто возможно путем отображения объектов из вашей области в линейное пространство. Например , вы можете увидеть, как это работает для встраивания слов в естественные языки ( учебник word2vec, перейдите к разделу «визуализация изученных встраиваний»). В этом случае сходство между объектами определяется расстоянием в линейном пространстве, которое очень быстро вычисляется.
Насколько сложным должно быть отображение в вашем случае, во многом зависит от ваших данных: насколько разнообразны диаграммы и какое сходство вы хотите захватить.
В вашем примере с двумя векторами можно вычислить одно значение: наклон линии регрессии . Это, вероятно, сработает, если ваши графики будут «somewhat linear» в природе. Если вы также хотите захватить синусоидальные паттерны, вы можете попытаться нормализовать временной ряд, вычитая первое значение. Опять же, в вашем конкретном примере он покажет идеальную посадку.
Итог: сложность отображения определяется сложностью данных.
Поделиться Maxim 22 сентября 2017 в 19:19
1
Если они всегда имеют одинаковую длину, корреляция Пирсона должна быть гораздо более подходящей и гораздо более быстрой.
Если вы стандартизируете свои векторы, Пирсон является евклидовым, и вы можете использовать любое многомерное дерево поиска для дальнейшего ускорения.
Поделиться Has QUIT—Anony-Mousse 26 сентября 2017 в 20:01
Похожие вопросы:
Когда был создан первый алгоритм обнаружения линий и когда была поставлена задача обнаружения линий?
Интересно, когда был создан первый алгоритм обнаружения линий (впервые использованный на практике и рефренированный любыми публикациями) и когда была поставлена проблема обнаружения линий (я знаю,…
Метрика для сравнения того, насколько похожи две линейные линии 2D
Есть ли алгоритм (предпочтительно в реализации C#), который позволяет мне сравнить, насколько похожи две строки? В моем случае у меня есть одна опорная линия, и у меня есть много вторичных линий,…
OpenCV алгоритм подгонки линии
Я пытаюсь понять алгоритм OpenCV fitLine(). Это фрагмент кода из OpenCV: icvFitLine2D функция — icvFitLine2D Я вижу, что существует некоторая случайная функция, которая выбирает точки для. ..
..
Нарисуйте вертикальную линию, когда две линии пересекаются в Highcharts
У меня есть график температурной линии, и я хочу нарисовать красную вертикальную линию, когда две температуры (температура поверхности и точка росы) пересекаются. Пока что я рисую вертикальный…
Алгоритм поиска того, где именно две строки совпадают/отличаются
Я работаю над поиском сходства/различий в исходном коде различных программ java. Я использовал реализацию алгоритма Левенштейна, чтобы найти, насколько похожи две программы. Я хочу знать, есть ли…
почему алгоритм крускала и алгоритм Дейкстры так похожи друг на друга?
Я знаю, что эти два алгоритма используются для решения различных задач, алгоритм Дейкстры используется для поиска кратчайшего пути в графе, в то время как алгоритм крускала используется для поиска…
как я могу сравнить две изогнутые линии на двух картинках?
У меня есть 2 изображения,на которых есть две линии, я хочу сравнить там две изогнутые линии и узнать, насколько они похожи together. ..I используйте Mathlab для программирования, а также используйте…
..I используйте Mathlab для программирования, а также используйте…
Есть ли способ поместить линии сетки поверх контурного участка?
Я использую функцию contourf для создания контурного графика: Я хотел бы, чтобы линии сетки появлялись поверх плоскости, которая показывает контуры. Я наткнулся на одно решение, но оно работает…
алгоритм bresenham для линии, используя javascript
Я пытаюсь реализовать алгоритм бресенхэма для линии вот что я сделал: https://jsfiddle.net/noatendler/u2vnz5La/1/ по какой-то причине линия находится не в той точке, где я нажал Я просмотрел…
Соедините две линии зигзагообразными линиями
У меня две точки на плоскости XZ, л аргер/самая высокая точка равна L=(х, л , з л ) и меньше/короче точка Х=(Х , З ) Соединяя точки L и S с линией Z=0, я получаю две линии Я намерен соединить две…
Графические методы анализа данных
Графические методы анализа данныхГрафические методы анализа данных
Краткий обзор типов графиков
Типичные методы визуализации
Категоризованные графики
Одним из наиболее мощных аналитических методов
исследования является разделение
(«разбиение») данных на группы для сравнения
структуры получившихся подмножеств. Эти методы
широко применяются как в разведочном
анализе данных, так и при проверке гипотез и
известны под разными названиями (классификация,
группировка, категоризация, разбиение,
расслоение и пр.). Например, взаимосвязь между
возрастом и риском инфаркта может отличаться для
мужчин и женщин (для мужчин эта зависимость
сильнее). Или например, зависимость между приемом
лекарств и снижением уровня холестерина может
наблюдаться только для женщин с пониженным
давлением и в возрасте 30-40 лет.
Производительность или гистограммы
мощности могут различаться для временных
промежутков, когда управление осуществляется
разными операторами. Разным экспериментальным
группам также могут соответствовать разные
наклоны линий регрессии.
Эти методы
широко применяются как в разведочном
анализе данных, так и при проверке гипотез и
известны под разными названиями (классификация,
группировка, категоризация, разбиение,
расслоение и пр.). Например, взаимосвязь между
возрастом и риском инфаркта может отличаться для
мужчин и женщин (для мужчин эта зависимость
сильнее). Или например, зависимость между приемом
лекарств и снижением уровня холестерина может
наблюдаться только для женщин с пониженным
давлением и в возрасте 30-40 лет.
Производительность или гистограммы
мощности могут различаться для временных
промежутков, когда управление осуществляется
разными операторами. Разным экспериментальным
группам также могут соответствовать разные
наклоны линий регрессии.
Для количественного описания различий между
группами наблюдений разработаны многочисленные
вычислительные методы, основанные на
группировке данных (например, дисперсионный
анализ). Однако графические средства (такие как
рассматриваемые в этом разделе категоризованные
графики) дают особые преимущества и
позволяют выявить закономерности, которые
трудно поддаются количественному описанию и
которые весьма сложно обнаружить с помощью
вычислительных процедур (например, сложные
взаимосвязи, исключения или аномалии). В этих
случаях графические методы предоставляют
уникальные возможности многомерного
аналитического исследования или «добычи» данных.
Однако графические средства (такие как
рассматриваемые в этом разделе категоризованные
графики) дают особые преимущества и
позволяют выявить закономерности, которые
трудно поддаются количественному описанию и
которые весьма сложно обнаружить с помощью
вычислительных процедур (например, сложные
взаимосвязи, исключения или аномалии). В этих
случаях графические методы предоставляют
уникальные возможности многомерного
аналитического исследования или «добычи» данных.
Что такое категоризованные графики
Термин «категоризованные графики» впервые
был использован в программе STATISTICA компании
StatSoft в 1990 году (кроме того, Becker, Cleveland и Clark из Bell Labs
называют их графиками на решетке). Эти
графики представляют собой наборы двумерных,
трехмерных, тернарных или n-мерных графиков
(таких как гистограммы,
диаграммы рассеяния,
линейные графики, поверхности,
тернарные
диаграммы рассеяния и пр. ), по одному графику
для каждой выбранной категории
(подмножества) наблюдений, например,
опрашиваемых из Нью-Йорка, Чикаго или Далласа.
Эти «входящие» графики располагаются
последовательно в одном графическом окне,
позволяя сравнивать структуру данных для каждой
из указанных подгрупп (например, городов).
), по одному графику
для каждой выбранной категории
(подмножества) наблюдений, например,
опрашиваемых из Нью-Йорка, Чикаго или Далласа.
Эти «входящие» графики располагаются
последовательно в одном графическом окне,
позволяя сравнивать структуру данных для каждой
из указанных подгрупп (например, городов).
Для выбора подгрупп можно использовать множество методов, самый простой из них — это введение категориальной переменной (например, переменной City с значениями New York, Chicago и Dallas). На следующем графике показаны гистограммы переменной, представляющей данные о самооценке стресса жителями каждого из трех городов.
На основе этих данных можно сделать вывод о том, что жители Далласа не очень подвержены стрессам, в то время как распределения уровня стресса в Нью-Йорке и Чикаго довольно похожи.
Некоторые программы (например, система STATISTICA)
поддерживают двухвходовую или многомерную
категоризацию, где для задания подгрупп
используется не один (например, City), а два или
более критериев (например, City и Time ). Двухвходовые категоризованные графики можно
рассматривать как «таблицы графиков», где
каждый входящий график находится на
«пересечении» определенных значений первой
(например, City) и второй (например, Time) группирующих
переменных.
Двухвходовые категоризованные графики можно
рассматривать как «таблицы графиков», где
каждый входящий график находится на
«пересечении» определенных значений первой
(например, City) и второй (например, Time) группирующих
переменных.
Добавление второго фактора показывает, что картины стрессовых нагрузок в Нью-Йорке и Чикаго в действительности сильно различаются, если учитывается время опроса, в то время как фактор времени практически ничего не меняет в Далласе.
Категоризованные и матричные графики. Матричные графики
также состоят из нескольких графиков; однако
здесь каждый из них основывается (или может
основываться) на одном и том же множестве
наблюдений, и графики строятся для всех
комбинаций переменных из одного или двух
списков. Для категоризованных графиков
требуется такой же выбор переменных, как и для
некатегоризованных графиков соответствующего
типа (например, две переменных для диаграммы
рассеяния). В то же время для категоризованных
графиков необходимо указать по крайней мере одну
группирующую
переменную (или способ разбиения наблюдений
на категории), где содержалась бы информация о
принадлежности каждого наблюдения к
определенной подгруппе (например, Chicago, Dallas).
Группирующая
переменная не будет непосредственно
изображена на графике (т.е. не будет построена),
однако она будет служить критерием для
разделения всех анализируемых наблюдений на
отдельные подгруппы. Как показано выше, для
каждой группы (категории), определяемой
группирующей переменной, будет построен один
график.
В то же время для категоризованных
графиков необходимо указать по крайней мере одну
группирующую
переменную (или способ разбиения наблюдений
на категории), где содержалась бы информация о
принадлежности каждого наблюдения к
определенной подгруппе (например, Chicago, Dallas).
Группирующая
переменная не будет непосредственно
изображена на графике (т.е. не будет построена),
однако она будет служить критерием для
разделения всех анализируемых наблюдений на
отдельные подгруппы. Как показано выше, для
каждой группы (категории), определяемой
группирующей переменной, будет построен один
график.
Общие и независимые шкалы. Каждый элементарный график, входящий в состав категоризованного графика, может быть масштабирован в соответствии со своим собственным диапазоном значений (независимые шкалы).
Или все графики могут иметь общую шкалу,
достаточно широкую, чтобы охватить весь диапазон
значений.
Общий масштаб позволяет сравнивать диапазоны и распределения значений разных категорий. Однако, если эти диапазоны сильно различаются (что приводит к очень большой общей шкале), то исследование некоторых графиков может быть затруднено. Использование независимого масштаба может упростить выявление трендов и определенных закономерностей внутри категорий, но в то же время затруднить сравнение диапазонов значений разных подгрупп.
Методы категоризации
Существует пять основных методов
категоризации значений, которые будут кратко
описаны в этом разделе: целые числа, категории,
границы, коды и сложные подгруппы. Обратите
внимание, что одни и те же методы категоризации
можно использовать как для разбиения наблюдений
по входящим графикам, так и для категоризации
наблюдений внутри входящих графиков ( например,
на гистограммах
или диаграммах
размаха).
Целые числа. При использовании этого режима для определения категорий будут использованы целые значения выбранной группирующей переменной, и для всех наблюдений, принадлежащих каждой категории (заданной этими целыми числами), будет построено по одному графику. Если выбранная группирующая переменная содержит не целочисленные значения, то программа автоматически округлит каждое значение выделенной переменной до целого числа.
Категории. В этом режиме категоризации нужно указать желаемое число категорий. Программа разделит весь диапазон значений выбранной группирующей переменной (от минимального до максимального) на указанное число интервалов равной длины.
Границы. Метод границ также представляет
собой интервальную категоризацию, однако в этом
случае интервалы могут иметь произвольную
(например, различную) длину, определяемую
пользователем (например, «меньше -10»,
«больше или равно -10, но меньше 0», «больше
или равно 0, но меньше 10» и «больше или равно
10»).
Коды. Этот метод следует использовать в том случае, если выбранная группирующая переменная содержит «коды » (т.е. особые смысловые значения, такие как Male, Female), по которым можно разбить данные на категории.
Сложные подгруппы. Этот метод дает возможность пользователю использовать для выделения подгрупп более одной переменной. Другими словами, категоризация, основанная на выделении сложных подгрупп, может представлять не распределения конкретных переменных, а распределения частот определенных «событий» при заданной комбинации значений любого числа переменных текущего набора данных. Например, можно указать шесть категорий, задаваемых комбинациями значений трех переменных Gender, Age и Employment.
Гистограммы
Гистограммы
используются для изучения распределений частот
значений переменных. Такое частотное
распределение показывает, какие именно
конкретные значения или диапазоны значений
исследуемой переменной встречаются наиболее
часто, насколько различаются эти значения,
расположено ли большинство наблюдений около среднего значения,
является распределение симметричным
или асимметричным, многомодальным
(т.е. имеет две или более вершины) или одномодальным и
т.д. Гистограммы
также используются для сравнения наблюдаемых и
теоретических или ожидаемых распределений.
Такое частотное
распределение показывает, какие именно
конкретные значения или диапазоны значений
исследуемой переменной встречаются наиболее
часто, насколько различаются эти значения,
расположено ли большинство наблюдений около среднего значения,
является распределение симметричным
или асимметричным, многомодальным
(т.е. имеет две или более вершины) или одномодальным и
т.д. Гистограммы
также используются для сравнения наблюдаемых и
теоретических или ожидаемых распределений.
Категоризованные гистограммы представляют собой наборы гистограмм, соответствующих различным значениям одной или нескольких категоризующих переменных или наборам логических условий категоризации (см. Методы категоризации).
Частотные распределения могут представлять интерес по двум основным причинам.
- По форме распределения можно судить о природе
исследуемой переменной (например, бимодальное
распределение позволяет предположить, что
выборка не является однородной и содержит
наблюдения, принадлежащие двум различным
множествам, которые в свою очередь нормально
распределены).

- Многие статистики основываются на определенных предположениях о распределениях анализируемых переменных; гистограммы позволяют проверить, выполняются ли эти предположения.
Как правило, работа с новым набором данных начинается с построения гистограмм всех переменных.
Гистограммы и группировка. Категоризованные
гистограммы предоставляют такую же информацию о
данных, как и группировка (например, среднее, медиану, минимум,
максимум, разброс и т.п.; см. главу Основные
статистики и таблицы). Хотя конкретные
(числовые) значения описательных статистик легко
увидеть в таблице, в то же время общую структуру и
глобальные характеристики распределения проще
изучать на графике. Более того, график дает
качественную информацию о распределении,
которую невозможно отразить с помощью
какого-либо одного параметра. Например, по асимметрии
распределения значений дохода можно сделать
вывод о том, что большинство населения имеет
низкий, а не высокий уровень доходов. Если помимо
этого провести группировку данных по
этническому и половому признакам, то можно
обнаружить, что в некоторых подгруппах эта
структура распределения станет еще более ярко
выраженной. Хотя эта информация содержится в
значении коэффициента асимметрии
(для каждой подгруппы), но она легче
воспринимается и запоминается, будучи
графически представленной на гистограмме. Кроме
того, на гистограмме можно наблюдать некоторые
«впадины и выпуклости», которые могут
свидетельствовать о социальном расслоении в
исследуемой группе населения или об аномалиях в
распределении дохода отдельных подгрупп,
связанных с недавней налоговой реформой.
Если помимо
этого провести группировку данных по
этническому и половому признакам, то можно
обнаружить, что в некоторых подгруппах эта
структура распределения станет еще более ярко
выраженной. Хотя эта информация содержится в
значении коэффициента асимметрии
(для каждой подгруппы), но она легче
воспринимается и запоминается, будучи
графически представленной на гистограмме. Кроме
того, на гистограмме можно наблюдать некоторые
«впадины и выпуклости», которые могут
свидетельствовать о социальном расслоении в
исследуемой группе населения или об аномалиях в
распределении дохода отдельных подгрупп,
связанных с недавней налоговой реформой.
Категоризованные гистограммы и диаграммы
рассеяния. Полезное применение категоризации
для непрерывных переменных — это представление
взаимосвязи трех переменных одновременно. Ниже
показана диаграмма рассеяния для двух
переменных Load 1 и Load 2.
Предположим, к ним нужно добавить третью переменную (Output) и исследовать ее распределение при различных значения совместного распределения переменных Load 1 и Load 2. Для этого можно построить следующий график:
На этом графике обе переменные Load 1 и Load 2 сгруппированы в 5 интервалов, и для каждой комбинации этих интервалов вычислено распределение переменной Output. Обратите внимание, что внутри «прямоугольника» (параллелограмма) находятся наблюдения, одинаковые для обоих показанных выше графиков.
Диаграммы рассеяния
Двумерные диаграммы
рассеяния используются для визуализации
взаимосвязей между двумя переменными X и Y
(например, весом и ростом). На этих диаграммах
отдельные точки данных представлены маркерами
на плоскости, где оси соответствуют переменным.
Две координаты (X и Y), определяющие положение
точки, соответствуют значениям переменных. Если
между переменными существует сильная
взаимосвязь, то точки на графике образуют
упорядоченную структуру (например, прямую линию
или характерную кривую). Если переменные не
взаимосвязаны, то точки образуют «облако».
Если
между переменными существует сильная
взаимосвязь, то точки на графике образуют
упорядоченную структуру (например, прямую линию
или характерную кривую). Если переменные не
взаимосвязаны, то точки образуют «облако».
Можно построить также категоризованные диаграммы рассеяния, сгруппированные по значениям одной или нескольких переменных, а с помощью метода сложных подгрупп (см. Методы категоризации) — диаграммы рассеяния, категоризованные по заданным логическим условиям выбора подгрупп наблюдений.
Категоризованные диаграммы рассеянияпредставляют собой мощный исследовательский и аналитический метод для изучения взаимосвязей между двумя и более переменными среди различных подгрупп.
Однородность двумерных распределений (форма
взаимосвязей).Диаграммы
рассеяния обычно используются для выявления
природы взаимосвязи двух переменных (например,
кровяного давления и уровня холестерина),
поскольку они предоставляют гораздо больше
информации, чем коэффициент корреляции.
Например, неоднородность выборки, по которой рассчитываются корреляции, может привести к искажению значений коэффициента корреляции. Предположим, коэффициент корреляции рассчитывается по данным, полученным в двух экспериментальных группах, но этот факт при вычислениях игнорируется. Пусть эксперимент в одной из подгрупп привел к увеличению значений обеих переменных, и на диаграмме рассеяния данные из каждой группы образуют отдельные «облака» (как показано на картинке).
В этом примере большое значение коэффициента корреляции целиком обусловлено распределением по группам и не отражает «истинную» взаимосвязь между двумя переменными, которая практически близка к 0 (это хорошо видно, если рассматривать каждую группу отдельно).
Если вы предполагаете, что подобная структура
присутствует и в ваших данных, и знаете, каким
образом выделить «подгруппы» наблюдений, то
имеет смысл построить категоризованную
диаграмму рассеяния.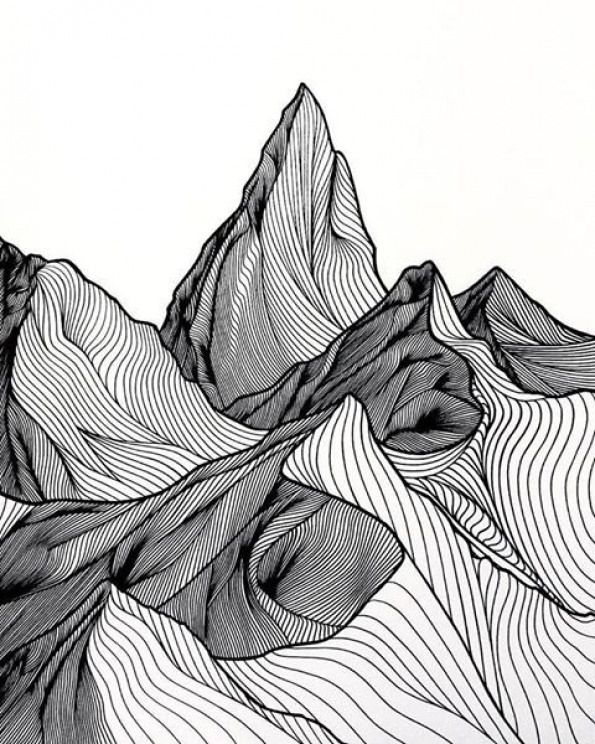
Такой график поможет вам прояснить структуру взаимосвязей между переменными X и Y внутри каждой подгруппы (после соответствующего разбиения наблюдений).
Нелинейные зависимости. С помощью диаграмм рассеяния можно исследовать и нелинейные взаимосвязи между переменными. При этом не существует каких-либо «автоматических» или простых способов оценки нелинейности. Стандартный коэффициент корреляции Пирсона r позволяет оценить только линейность связи, а некоторые непараметрические корреляции, например, Спирмена R, дают возможность оценить нелинейность, но только для монотонных зависимостей. На диаграммах рассеяния можно изучить структуру взаимосвязей, чтобы затем с помощью преобразования привести данные к линейному виду или выбрать подходящую нелинейную подгонку.
Дополнительную информацию можно найти в
разделах Основные статистики, Непараметрическая статистика и
распределения, Множественная
регрессия и Нелинейное
оценивание.
Вероятностные графики
Существует три типа категоризованных вероятностных графиков: нормальные, полунормальные и с исключенным трендом. Нормальные вероятностные графики — это быстрый способ визуальной проверки степени соответствия данных нормальному распределению.
В свою очередь категоризованные вероятностные графики дают возможность исследовать близость к нормальному распределению различных подгрупп данных .
Категоризованные нормальные вероятностные графики представляют собой эффективный инструмент для исследования однородности группы наблюдений с точки зрения соответствия нормальному распределению.
Графики квантиль-квантиль
Категоризованные графики
квантиль-квантиль (или К-К) используются для
поиска в определенном семействе распределений
того распределения, которое наилучшим образом
описывает имеющиеся данные.
В случае категоризованных графиков К-К строится набор графиков квантиль-квантиль, по одному для каждого значения категориальных переменных (X или X и Y) или для заданных условий выбора сложных подгрупп (см. Методы категоризации). Для графиков К-К используются следующие семейства распределений: экспоненциальное, экстремальное, нормальное, Релея, бета-, гамма-, логнормальное и Вейбулла.
Графики вероятность-вероятность
Категоризованные графики вероятность-вероятность (или В-В) используются для проверки соответствия конкретного теоретического распределения имеющимся исходным данным. На этих графиках для каждого значения категориальных переменных (X или X и Y) или для заданных условий выбора сложных подгрупп (см. Методы категоризации) создается по одному графику вероятность-вероятность.
На графиках В-В строится наблюдаемая функция
распределения (доля непропущенных значений x) в зависимости от
теоретической функции распределения, чтобы
оценить соответствие этой теоретической функции
наблюдаемым данным. Если все точки этого графика
располагаются на диагонали (содержащей точку 0 и
имеющей наклон 1), то можно заключить, что
наблюдаемое распределение хорошо
аппроксимируется данной теоретической функцией.
Если все точки этого графика
располагаются на диагонали (содержащей точку 0 и
имеющей наклон 1), то можно заключить, что
наблюдаемое распределение хорошо
аппроксимируется данной теоретической функцией.
Если не все точки данных располагаются на диагональной линии, то на таком графике можно визуально выделить группы наблюдений, соответствующие и не соответствующие искомому распределению (если, к примеру, точки образуют кривую S-образной формы вокруг диагональной линии, то к ним можно применить определенное преобразование для приведения к нужной форме распределения).
Линейные графики
На линейных
графиках отдельные точки данных
соединяются линиями. Это простой способ
визуального представления последовательности
значений (например, цены на фондовом рынке за
несколько дней торгов). Категоризованные
линейные графики строятся в том случае, если
необходимо разбить данные на несколько групп
(категоризовать) с помощью группирующей
переменной (например, цены при закрытии
рынка по понедельникам, вторникам и т. д.) или с
помощью логических условий, составленных по
нескольким переменным (например, цены при
закрытии рынка в те дни, когда две другие акции и
индекс Доу Джонса выросли по сравнению с другими
ценами закрытия; см. Методы
категоризации).
д.) или с
помощью логических условий, составленных по
нескольким переменным (например, цены при
закрытии рынка в те дни, когда две другие акции и
индекс Доу Джонса выросли по сравнению с другими
ценами закрытия; см. Методы
категоризации).
Диаграммы размаха
На диаграммах размаха (этот термин был впервые использован Тьюки в 1970 году) представлены диапазоны значений выбранной переменной (или переменных) для отдельных групп наблюдений. Для выделения этих групп используются от одной до трех категориальных (группирующих) переменных или набор логических условий выбора подгрупп.
Для каждой группы наблюдений вычисляется
центральная тенденция (медиана
или среднее), а также
размах или изменчивость (квартили,
стандартные ошибки
или стандартные
отклонения). Выбранные параметры отображаются
на графике одним из пяти способов (Прямоугольники-Отрезки,
Отрезки, Прямоугольники, Столбцы или
Верхние-нижние засечки). На этом графике можно
показать и выбросы (см. разделы о выбросах и крайних точках).
На этом графике можно
показать и выбросы (см. разделы о выбросах и крайних точках).
На следующем графике, например, выбор факторов можно было бы считать вполне удачным, если бы не «досадное» несоответствие, на которое указывают выделенные на рисунке выбросы (в данном случае это значения, попадающие за пределы 1,5 квартильных размахов):
А на следующем рисунке не показаны ни выбросы, ни крайние точки.
Можно выделить два основных направления
использования диаграмм
размаха: (a) отображение диапазонов значений
отдельных элементов, наблюдений или выборок
(например, типичные минимаксные графики цен на
акции или товары или графики агрегированных
данных с диапазонами), (б) отображение изменения
значений в отдельных группах или выборках
(например, когда точкой внутри прямоугольника
представлено среднее
значение для каждой выборки, сам прямоугольник
соответствует значениям стандартной ошибки, а
меньший прямоугольник или пара «отрезков»
обозначает стандартное
отклонение от среднего).
С помощью диаграмм размаха, на которых представлены характеристики изменчивости, можно быстро оценить и «интуитивно представить» силу связи между группирующей и зависимой переменной. Предположив, что зависимая переменная нормально распределена, и зная долю наблюдений, попадающих, к примеру, в интервал ±1 или ±2 стандартных отклонения от среднего (см. Элементарные понятия статистики), можно сделать, например, вывод о том, что 95% наблюдений из экспериментальной группы 1 попадают в другой диапазон значений, нежели 95% наблюдений из группы 2.
На этих графиках можно изобразить и так называемые усеченные средние (этот термин был впервые использован Тьюки в 1962 году), которые вычисляются после исключения заданного пользователем процента наблюдений с концов (хвостов) распределения.
Круговые диаграммы
Одним из наиболее широко используемых типов
графического представления данных являются круговые диаграммы, на
которых показаны пропорции или сами значения
переменных. Категоризованные графики этого типа
состоят из нескольких круговых диаграмм, где
данные разделены по группам с помощью одной или
нескольких группирующих
переменных (например, gender) или
категоризованы согласно логическим условиям
выбора подгрупп (см. Методы
категоризации).
Категоризованные графики этого типа
состоят из нескольких круговых диаграмм, где
данные разделены по группам с помощью одной или
нескольких группирующих
переменных (например, gender) или
категоризованы согласно логическим условиям
выбора подгрупп (см. Методы
категоризации).
В дальнейшем, говоря о категоризации этих
графиков, мы будем иметь ввиду круговые диаграммы
частот (в противоположность круговым диаграммам
значений). Эти типы графиков, называемые также
частотными круговыми диаграммами, представляют
данные аналогично гистограммам.
Все значения выбранной переменной
категоризуются с помощью заданного метода
категоризации, а затем относительные значения
частот отображаются в виде сегментов круговой
диаграммы пропорционального размера. Таким
образом, эти графики являются альтернативным
представлением гистограммы частот (см. раздел
о категоризованных
гистограммах).
Диаграммы рассеяния круговых диаграмм. Еще одно очень полезное применение категоризованных круговых диаграмм — это представление относительных частот значений какой-либо переменной в различных «местах» совместного распределения двух других переменных. Например:
Обратите внимание, что круговые диаграммы изображены только в тех «местах», где имеются данные. Показанный выше график напоминает диаграмму рассеяния (переменных L1 и L2), где маркерами точек являются круговые диаграммы. Однако помимо обычной информации, содержащейся в диаграмме рассеяния, здесь в каждой точке дополнительно показано относительное распределение третьей переменной (а именно, доля значений Low, Medium и High Quality).
Графики пропущенных значений и данных вне диапазона
На этих графиках можно наглядно представить
структуру распределения точек данных,
содержащих пропущенные значения или находящихся
«вне диапазонов», заданных пользователем.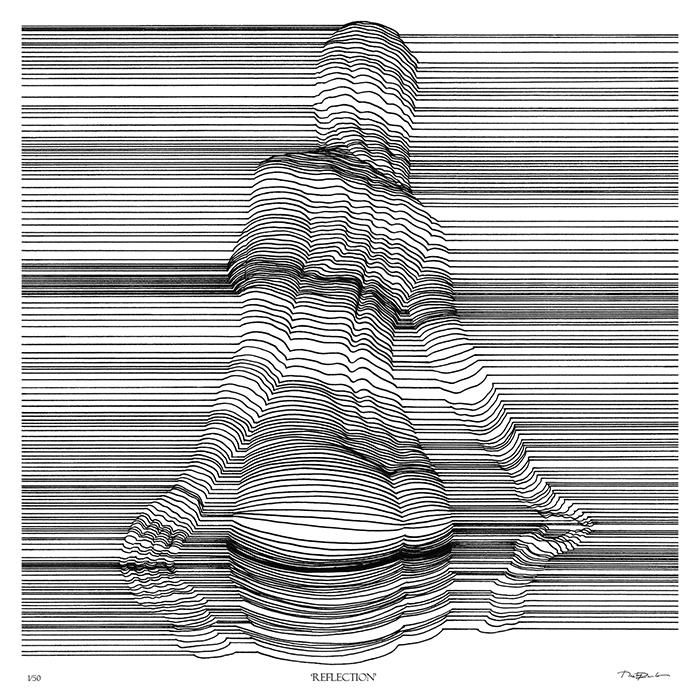 При этом строится по одной двумерной диаграмме
для каждой группы наблюдений, выделенной с
помощью группирующих
переменных или с помощью условий выбора
сложных подгрупп (см. Методы
категоризации).
При этом строится по одной двумерной диаграмме
для каждой группы наблюдений, выделенной с
помощью группирующих
переменных или с помощью условий выбора
сложных подгрупп (см. Методы
категоризации).
Эти типы графиков используются в разведочном анализе данных, чтобы определить, является ли случайным распределение точек с пропущенными значениями, а также для оценки их диапазона.
Трехмерные (3М) графики
Трехмерные
диаграммы рассеяния (пространственные,
спектральные, трассировочные и диаграммы отклонений),
карты линий уровня и
поверхности
также можно построить для подгрупп
наблюдений, заданных с помощью выбранной
категориальной переменной или логических
условий выбора (см. Методы
категоризации). Основная задача этих графиков -
упростить сравнение взаимосвязей между тремя и
более переменными для различных групп или
категорий наблюдений.
Применения. Трехмерные графики в координатах XYZ отображают взаимосвязи между тремя переменными. С помощью различных способов категоризации можно исследовать эти зависимости при различных условиях (т.е. в разных группах).
Изучая, например, показанный ниже категоризованный график поверхности, можно сделать вывод о том, что величина допуска прибора не влияет на измерения (переменные Depend1, Depend2 и Height), кроме случая, когда она 3.
Этот вывод становится еще более очевидным, если использовать вместо поверхности карту линий уровня.
Тернарные графики
Категоризованные тернарные
графики используются для исследования
взаимосвязей между тремя и более переменными,
три из которых представляют собой компоненты
смеси (т.е. для каждого наблюдения значения их
суммы являются постоянной величиной), при этом
отдельный график строится для каждого уровня группирующей
переменной.
Для построения тернарных графиков используется треугольная система координат на плоскости или в пространстве и строится зависимость между четырьмя (или более) переменными (компонентами X, Y и Z и откликами V1, V2 и т.д.). При этом накладываются ограничения на относительные значения каждой из компонент, чтобы они в сумме давали одинаковую величину для каждого наблюдения (например, 1).
На категоризованных тернарных графиках строится по одному графику для каждого значения группирующей переменной (или заданного пользователем подмножества данных), и все они отображаются в одном графическом окне, чтобы можно было сравнивать различные подгруппы наблюдений.
Применения. Эти графики применяются для
анализа результатов эксперимента, в котором
измеряемый отклик зависит от относительного
соотношения трех компонент (например, трех
химических веществ при составлении
смесей), которое варьируется с целью
определения его оптимального значения. Эти
типы графического представления можно
использовать и в других случаях, когда
взаимосвязь между переменными, на которые
наложены определенные ограничения, необходимо
исследовать для различных групп или категорий
наблюдений.
Эти
типы графического представления можно
использовать и в других случаях, когда
взаимосвязь между переменными, на которые
наложены определенные ограничения, необходимо
исследовать для различных групп или категорий
наблюдений.
Закрашивание
Закрашивание является одним из первых и, по-видимому, наиболее широко распространенных методов, известных как графический разведочный анализ данных. Этот метод позволяет интерактивно выделять на экране отдельные точки или подмножества данных и задавать их характеристики, или исследовать их влияние на взаимосвязи между переменными (например, на матрицах диаграмм рассеяния) и идентифицировать выбросы(например, с помощью меток).
Связи между переменными можно наглядно
представить с помощью аппроксимирующих функций
(например, двумерных кривых или трехмерных
поверхностей) и доверительных интервалов. Интерактивно удаляя или добавляя определенные
подгруппы наблюдений, можно наблюдать за
изменениями этих функций и их параметров. Одно из
применений метода закрашивания — это, например,
выделение на матричной
диаграмме рассеяния всех точек данных,
принадлежащих определенной категории (например,
на показанном ниже рисунке на правом верхнем
графике выделена группа наблюдений,
соответствующих значению «среднего» уровня
дохода).
Интерактивно удаляя или добавляя определенные
подгруппы наблюдений, можно наблюдать за
изменениями этих функций и их параметров. Одно из
применений метода закрашивания — это, например,
выделение на матричной
диаграмме рассеяния всех точек данных,
принадлежащих определенной категории (например,
на показанном ниже рисунке на правом верхнем
графике выделена группа наблюдений,
соответствующих значению «среднего» уровня
дохода).
Такое исследование помогает определить, как эти конкретные наблюдения влияют на связи между другими переменными того же набора данных (например, на корреляцию между «расходами» и «активами»).
В режиме «динамического закрашивания» (см.
следующий пример) или «автоматического
обновления функции подгонки» можно задать
движение кисти по определенным последовательным
диапазонам выбранной переменной (например,
непрерывной, а не дискретной, как на показанном
ранее примере) и исследовать динамику вклада
этой переменной в связи между другими
переменными этого набора данных.
Сглаживание двумерных распределений
Для наглядного представления таблицы значений двух переменных используются трехмерные гистограммы. Их можно рассматривать как объединение двух простых гистограмм для совместного анализа частот значений двух переменных. Чаще всего на этом графике для каждой «ячейки» таблицы нарисован один трехмерный столбец, а его высота соответствует частоте значений в этой ячейке. При построении трехмерной гистограммы для каждой из двух переменных можно использовать свой метод категоризации (см. ниже).
Когда предусмотрены процедуры сглаживания
данных, то трехмерное представление частот
значений можно аппроксимировать поверхностью.
Такое сглаживание можно осуществить для любой
трехмерной гистограммы. Для достаточно простой
структуры данных (как на предыдущем рисунке)
такое сглаживание не имеет особого смысла.
Однако, в случае более сложной картины распределения частот эта процедура может оказаться эффективным инструментом разведочного анализа данных
и позволит выявить особенности, которые трудно обнаружить на обычной трехмерной гистограмме (например, показанную выше «волновую структуру» поверхности).
Послойное сжатие
На графиках этого типа за счет сокращения области основного графика освобождается место для графиков на полях, которые располагаются в правой и верхней части графического окна (включая маленький угловой график). Эти графики на полях представляют собой соответственно вертикально и горизонтально сжатые изображения основного графика.
Послойное сжатие двумерных графиков является
методом разведочного анализа данных, который
дает возможность скрытые тренды и структуры
двумерных наборов данных. Рассмотрим следующий
рисунок.
Рассмотрим следующий
рисунок.
Здесь на примере, приведенном Кливландом (Cleveland, 1993), можно убедиться, что в каждом цикле солнечной активности число пятен уменьшается гораздо медленнее, чем нарастает в начале цикла. Такое поведение совершенно не очевидно при исследовании обычного линейного графика, в то время как сжатый график позволяет обнаружить эту скрытую картину.
Проекции трехмерных наборов данных
Полезным методом изучения и аналитического исследования структуры поверхности (созданной, как правило, по трехмерным наборам данных) является построение ее проекции на плоскость в виде карты линий уровня.
Эти графики менее эффективны для быстрого визуального анализа формы трехмерных структур по сравнению с графиками поверхности,
однако их преимущество заключается в возможности точного исследования формы поверхности —
на картах линий уровня отображается ряд не
искаженных горизонтальных «сечений».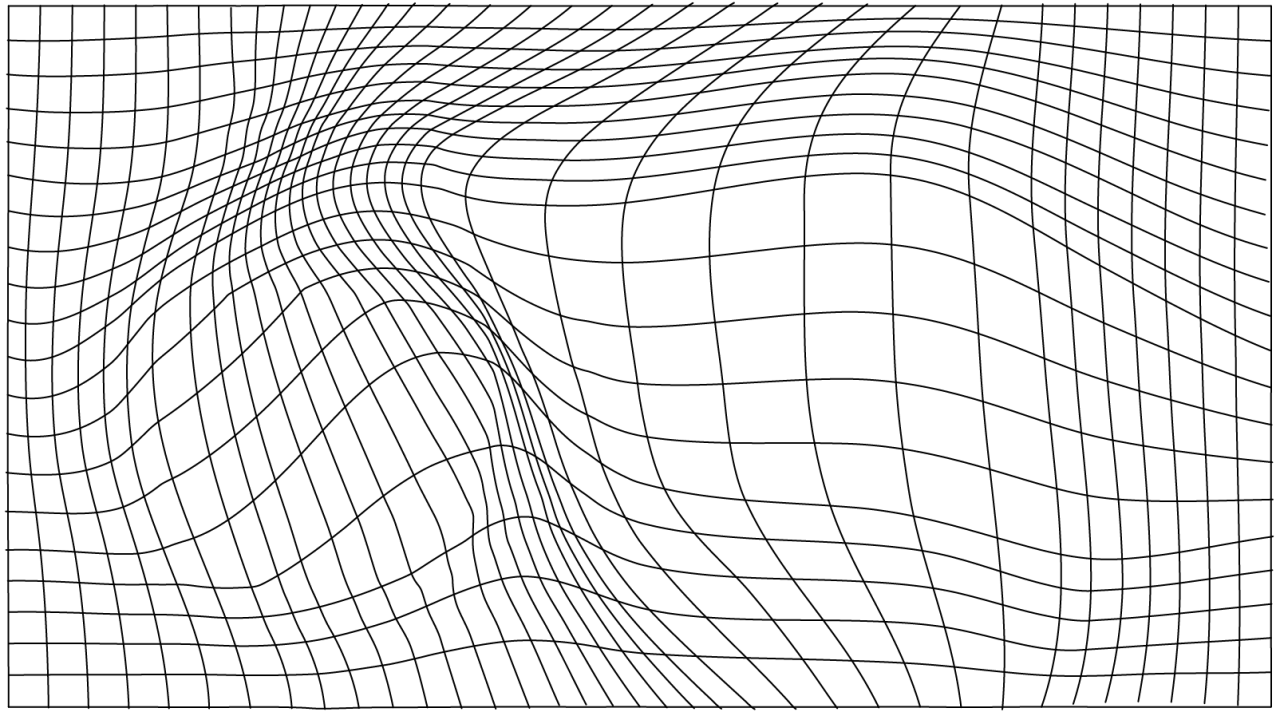
Пиктографики
На пиктографиках каждое наблюдение
представлено в виде многомерного символа, что
позволяет использовать эти типы графического
представления данных в качестве не очень
простого, но мощного исследовательского
инструмента. Главная идея такого метода анализа
основана на человеческой способности
«автоматически» фиксировать сложные связи
между многими переменными, если они проявляются
в последовательности элементов (в данном случае
«пиктограмм»). Иногда понимание (или
«чувство») того, что некоторые элементы
«чем-то похожи» друг на друга, приходит
раньше, чем наблюдатель (аналитик) может
объяснить, какие именно переменные
обусловливают это сходство (Lewicki, Hill, & Czyzewska, 1992).
Конкретную природу проявившихся взаимосвязей
между переменными позволяет выявить уже
последующий анализ данных, основанный на
изучении этого интуитивно обнаруженного
сходства.
Основная идея пиктографиков заключается в представлении элементарных наблюдений как отдельных графических объектов, где значения переменных соответствуют определенным чертам или размерам объекта (обычно одно наблюдение = одному объекту). Это соответствие устанавливается таким образом, чтобы общий вид объекта менялся в зависимости от конфигурации значений.
Таким образом, объекты имеют определенный «внешний вид», который уникален для каждой конфигурации значений и может быть идентифицирован наблюдателем. Изучение таких пиктограмм помогает выявить как простые связи, так и сложные взаимодействия между переменными.
Анализ пиктографиков
Целесообразно проводить анализ пиктографиков в пять этапов.
- Сначала выберите порядок анализируемых
переменных. В большинстве случаев наилучшим
вариантом оказывается случайная
последовательность.
 Кроме того, можно
попробовать расположить их в порядке,
соответствующем полученному уравнению множественной регрессии, факторным
нагрузкам или объясняемым факторам (см. главу Факторный анализ). Таким образом
можно упростить и сделать более
«однородным» общий вид пиктограмм, чтобы
легче идентифицировать слабо выраженные
различия. В то же время такой подход может
затруднить идентификацию некоторых структур. На
этом этапе можно дать только один универсальный
совет: прежде чем использовать какие-либо
сложные методы, попробуйте наиболее простой и
быстрый вариант, а именно, случайную
последовательность переменных.
Кроме того, можно
попробовать расположить их в порядке,
соответствующем полученному уравнению множественной регрессии, факторным
нагрузкам или объясняемым факторам (см. главу Факторный анализ). Таким образом
можно упростить и сделать более
«однородным» общий вид пиктограмм, чтобы
легче идентифицировать слабо выраженные
различия. В то же время такой подход может
затруднить идентификацию некоторых структур. На
этом этапе можно дать только один универсальный
совет: прежде чем использовать какие-либо
сложные методы, попробуйте наиболее простой и
быстрый вариант, а именно, случайную
последовательность переменных. - Попробуйте обнаружить какие-либо
закономерности, например, сходства между
группами пиктограмм, выбросы
или определенные связи между элементами
(например, » если первые два луча звезды
длинные, то как правило, с другой стороны есть
один или два коротких луча»).
 На этом этапе
лучше использовать пиктографики кругового
типа.
На этом этапе
лучше использовать пиктографики кругового
типа. - При обнаружении закономерностей постарайтесь сформулировать их в терминах конкретных переменных.
- Измените соответствие переменных и элементов пиктограмм (или переключитесь на один из последовательных пиктографиков), чтобы проверить обнаруженную структуру взаимосвязей (например, попробуйте переместить ближе друг к другу элементы, между которыми обнаружена связь). В некоторых случаях в конце этого этапа целесообразно исключить из рассмотрения те переменные, которые не вносят явного вклада в обнаруженную структуру.
- И наконец, используйте один из численных
методов (таких как регрессионный
анализ, нелинейное оценивание, дискриминантный или кластерный
анализ), чтобы проверить и попытаться
количественно оценить обнаруженные
закономерности или хотя бы их часть.

Систематизация пиктографиков
Большинство пиктографиков можно отнести к одной из двух групп: круговые и последовательные.
Круговые пиктографики. Круговые пиктографики (звезды, лучи, многоугольники) имеют вид «велосипедного колеса», на них значения переменных представлены расстояниями между центром пиктограммы («втулкой») и их концами.
Такие графики могут помочь в обнаружении связей между переменными, которые проявляются в общей структуре пиктограмм и зависят от конфигурации значений самих переменных.
Чтобы описать такую » общую картину» в терминах конкретных моделей или проверить имеющиеся предположения, имеет смысл использовать последовательные пиктографики, которые могут оказаться более эффективными, если уже известно, что именно требуется обнаружить.
Последовательные пиктографики.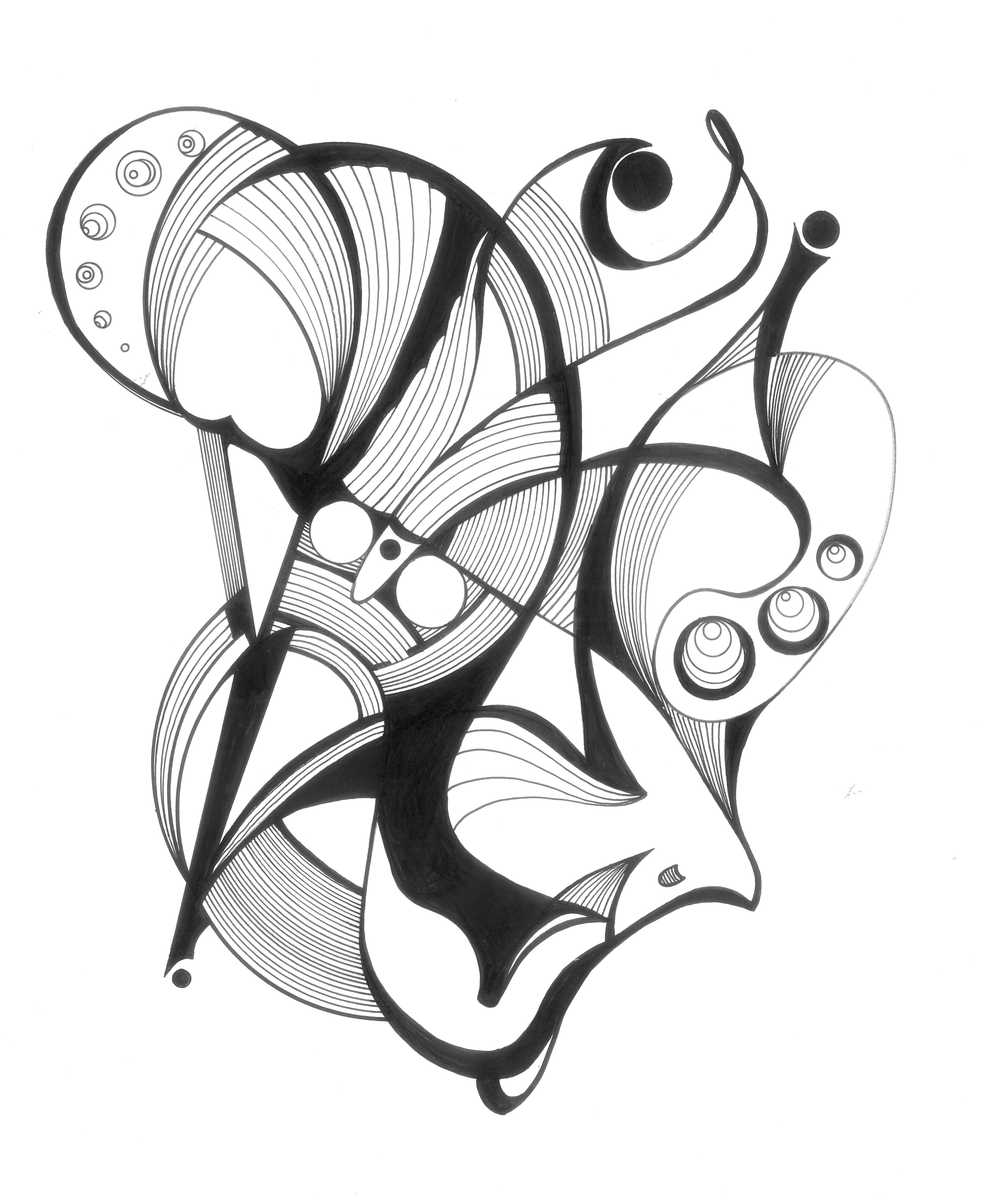 Последовательные пиктографики (столбцы, профили,
линии) представляют собой набор картинок с
маленькими последовательными графиками
(различных типов).
Последовательные пиктографики (столбцы, профили,
линии) представляют собой набор картинок с
маленькими последовательными графиками
(различных типов).
Значения переменных представлены здесь расстояниями между основанием пиктограммы и последовательными точками (например, высотами показанных выше столбцов). Эти графики менее эффективны на начальной стадии разведочного анализа, поскольку пиктограммы очень похожи между собой. Однако, как уже упоминалось ранее, такое представление может быть весьма полезным для проверки уже сформулированной гипотезы.
Пиктограммы круговых диаграмм. Эти пиктографики нельзя однозначно отнести к одной из двух групп. Все они имеют круговую форму, но в то же время последовательно разделены в соответствии с значениями переменных.
Их можно отнести скорее к последовательным, чем
к круговым пиктографикам, но можно использовать
и в том, и в другом случае.
«Лица Чернова». Этот тип пиктографиков составляет отдельную группу. Здесь каждое наблюдение представляет собой схематичное изображение лица, определенным чертам которого соответствуют относительные значения выбранных переменных.
Некоторые исследователи рассматривают этот способ графического представления данных как уникальный многомерный метод разведочного анализа, позволяющий выявить такие скрытые картины взаимосвязей между переменными, которые не могут быть обнаружены другими методами. Вероятно, такое заявление можно считать преувеличением. Кроме того, следует заметить, что этот способ исследования весьма непрост в применении и требует большого опыта в том, что касается сопоставления переменных чертам лица. См. также раздел Методы «добычи данных» .
Стандартизация значений
Как правило, при построении пиктографиков
значения переменных должны быть
стандартизованы, чтобы их можно было сравнивать
в пределах одной пиктограммы. Исключения
составляют те случаи, когда на пиктограммах
необходимо отобразить глобальные различия
диапазонов выбранных переменных. Поскольку
масштаб пиктограммы определяется наибольшим
значением, то на пиктограмме могут отсутствовать
те переменные, которые имеют значения другого
порядка малости, например, на пиктограмме звезды
некоторые лучи могут оказаться настолько
короткими, что совсем не будут видны..
Исключения
составляют те случаи, когда на пиктограммах
необходимо отобразить глобальные различия
диапазонов выбранных переменных. Поскольку
масштаб пиктограммы определяется наибольшим
значением, то на пиктограмме могут отсутствовать
те переменные, которые имеют значения другого
порядка малости, например, на пиктограмме звезды
некоторые лучи могут оказаться настолько
короткими, что совсем не будут видны..
Применения
Пиктографики обычно используются: (1) для обнаружения структур или кластеров наблюдений и (2) для исследования сложных взаимосвязей между несколькими переменными. Первый вариант соответствует кластерному анализу; т.е. процедуре классификации наблюдений.
Предположим, вы изучали характеры актеров и
записали их ответы на вопросы анкеты. С помощью
пиктографика можно определить, существуют ли
группы артистов, которые отличаются по их
ответам на заданные вопросы (можно, к примеру,
обнаружить, что некоторые артисты являются
творческими, недисциплинированными и
независимыми личностями, в то время как другая
группа состоит из умных, дисциплинированных
людей, которые ценят свою популярность).
Другая область применений — изучение взаимосвязей между переменными — напоминает факторный анализ, который используется для исследования вопроса о зависимости переменных. Предположим, изучалось мнение группы людей о различных марках автомобилей. В файле данных записаны средние оценки по каждому из свойств (рассматриваемых как переменные) для каждого из автомобилей (рассматриваемых как наблюдения).
При изучении «лиц Чернова» (где каждое лицо
представляет мнение об одном из автомобилей)
может оказаться, что улыбающиеся лица обычно
имеют большие уши; при этом, если цене
соответствует «ширина» улыбки, а
динамическим качествам — размер ушей, то это
«открытие» означает, что быстрые машины
являются более дорогими. Разумеется, это очень
простой пример; однако при реальном анализе
данных применение этого метода может сделать
более очевидными сложные взаимосвязи между
многими переменными.
Близкие способы графического представления
Связи между переменными из одного или двух списков могут быть представлены на матричных графиках. Использование матричных графиков одновременно с выделением подгрупп позволяет получить информацию, подобную той, которая отображается на пиктографиках.
Если использовать методы выделения подгрупп на диаграммах рассеяния, то для исследования взаимосвязей между двумя переменными можно использовать обычные 2М диаграммы рассеяния; а в случае трех переменных — 3Мдиаграммы рассеяния.
Типы графиков
Существуют различные типы пиктографиков.
«Лица Чернова». Для каждого наблюдения
рисуется отдельное «лицо»; при этом
относительные значения выбранных переменных
соответствуют форме и размерам определенных его
черт (например, длине носа, изгибу бровей, ширине
лица).
Дополнительно см. абзац «Лица Чернова» в разделе Систематизация пиктографиков.
Звезды. Это пиктографики кругового типа. Для каждого наблюдения рисуется пиктограмма в виде звезды; относительные значения выбранных переменных соответствуют относительным длинам лучей каждой звезды (по часовой стрелке, начиная с 12:00). Концы лучей соединены линиями.
Лучи. Эти пиктографики также относятся к круговому типу. Для каждого наблюдения строится одна пиктограмма. Каждый луч соответствует одной из выбранных переменных (по часовой стрелке, начиная с 12:00), и на нем отложено значение соответствующей переменной. Эти значения соединены линиями.
Многоугольники. Это пиктографикикругового типа. Для каждого
наблюдения рисуется отдельный многоугольник;
относительные значения выбранных переменных
соответствуют расстояниям вершин от центра
многоугольника (по часовой стрелке, начиная с
12:00).
Круговые диаграммы. Это пиктографики кругового типа. Для каждого наблюдения рисуется круговая диаграмма; относительные значения выбранных переменных соответствуют размерам сегментов диаграммы (по часовой стрелке, начиная с 12:00).
Столбцы. Это пиктографики последовательного типа. Для каждого наблюдения строится столбчатая диаграмма; относительные значения выбранных переменных соответствуют высотам последовательных столбцов.
Линии. Это пиктографики последовательного типа.
Для каждого наблюдения строится линейный график; относительные значения выбранных переменных соответствуют расстояниям точек излома линии от основания графика.
Профили. Это пиктографики последовательного
типа. Для каждого наблюдения строится зонный
график; относительные значения выбранных
переменных соответствуют расстояниям
последовательных пиков сечения над линией
основания.
Маркировка пиктограмм
Если программа позволяет вам выделять подгруппы наблюдений, то это свойство можно использовать и для маркировки соответствующих пиктограмм. При этом вокруг выделенных пиктограмм будут нарисованы рамки.
Шаблоны рамок, идентифицирующих заданные подгруппы, будут показаны в условных обозначениях рядом с текстом соответствующих условий выбора наблюдений. На следующем графике показан пример маркированных подгрупп.
Все наблюдения, удовлетворяющие условию для подгруппы 1 (значение переменной Iristype равно значению переменной Setosa и номер наблюдения меньше 100), обозначены специальной рамкой вокруг пиктограммы.
А все наблюдения, которые удовлетворяют
условию для подгруппы 2 (значение переменной Iristype
равно значению переменной Virginic и номер
наблюдения меньше 100), обозначены на графике
рамкой другого цвета.
Выборка данных
Иногда отображение на графике слишком большого числа точек данных затрудняет изучение их структуры (см. следующий рисунок). Если файл данных слишком большой, то имеет смысл показать на графике лишь подмножество наблюдений, чтобы общая картина не была скрыта маркерами точек.
Некоторые программы предлагают методы выборки (или оптимизации) данных, которые в ряде случаев могут оказаться весьма полезны. При этом пользователь может задать целое число n, меньшее числа наблюдений в файле данных, а программа случайным образом выберет из этого файла приблизительно n допустимых наблюдений и именно их построит на графике.
Заметим, что такие методы сокращения набора
данных (или размера выборки) эффективно
отображают случайную структуру этих данных.
Очевидно, эти методы принципиально отличаются от
методов выделения конкретного подмножества или
подгруппы наблюдений с помощью определенных
критериев (например, по полу, области или уровню
холестерина). Последние можно применять
интерактивно (например, в режиме динамического закрашивания)
или каким-либо другим способом (например, на категоризованных
графиках или с помощью условий выбора
наблюдений). Все эти методы в равной мере могут
помочь в идентификации сложной структуры
большого набора данных.
Последние можно применять
интерактивно (например, в режиме динамического закрашивания)
или каким-либо другим способом (например, на категоризованных
графиках или с помощью условий выбора
наблюдений). Все эти методы в равной мере могут
помочь в идентификации сложной структуры
большого набора данных.
Вращение (в трехмерном пространстве)
Изменение угла зрения при отображении трехмерной диаграммы рассеяния (простой, спектральной или пространственной) может оказаться эффективным средством для выявления некоторой структуры, которая видна только при определенном повороте «облака» точек (см. следующий рисунок).
Некоторые программы предоставляют полезный
инструмент для интерактивного изменения
перспективы и вращения изображения. Эти средства
контроля изображения позволяют подобрать
подходящий угол зрения и перспективу, чтобы
найти наиболее удачное расположение «точки
зрения» на график, а также дают возможность
управлять его вращением в горизонтальной и
вертикальной плоскости.
Эти инструменты могут оказаться весьма полезными не только при начальном разведочном анализе данных, но и при исследовании факторного пространства (см.Факторный анализ) или пространства размерностей (см. Многомерное шкалирование).
Все права на материалы электронного учебника принадлежат компании StatSoft
%d0%bb%d0%b8%d0%bd%d0%b8%d1%8f %d0%b3%d1%80%d0%b0%d1%84%d0%b8%d0%ba%d0%b8 PNG, векторы, PSD и пнг для бесплатной загрузки
поп арт 80 х патч стикер
3508*2480
Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов
4167*4167
естественный цвет bb крем цвета
1200*1200
поп арт 80 х патч стикер
3508*2480
Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации
4167*4167
аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс
5000*5000
Мемфис бесшовные модели 80 х 90 х стилей
4167*4167
поп арт 80 х патч стикер
2292*2293
три группы 3d реалистичное декоративное яйцо с золотым цветом на гнезде bd с золотым всплеском текстовый баннер
5000*5000
поп арт 80 х патч стикер
2292*2293
схема бд электронный компонент технологии принципиальная схема технологическая линия
2000*2000
милая ретро девушка 80 х 90 х годов
800*800
рисованной радио 80 х
1200*1200
80 летний юбилей дизайн шаблона векторные иллюстрации
4083*4083
поп арт 80 х патч стикер
3508*2480
диско дизайн в стиле ретро 80 х неон
5556*5556
поп арт 80 х патч стикер
3508*2480
поп арт 80 х патч стикер
3508*2480
80 е брызги краски дизайн текста
1200*1200
поп арт 80 х патч стикер
3508*2480
3d модель надувной подушки bb cream
2500*2500
Дизайн персонажей моды 80 х годов может быть коммерческими элементами
2000*2000
ма дурга лицо индуистский праздник карта
5000*5000
поп арт 80 х патч стикер
3508*2480
Косметический bb Крем Дизайн Плаката косметический Косметика постер Реклама косметики Плакат
3240*4320
поп арт 80 х патч стикер
3508*2480
Мода стерео ретро эффект 80 х годов тема искусства слово
1200*1200
Мемфис шаблон 80 х 90 х годов на белом фоне векторная иллюстрация
4167*4167
мемфис бесшовной схеме 80s 90 все стили
4167*4167
Неоновый эффект 80 х годов Ретро вечеринка арт дизайн
1200*1200
bb крем ню макияж косметика косметика
1200*1500
Ретро ретро пиксель
4725*2658
Ретро мода 80 х градиент цвета художественного слова
1200*1200
80 х годов ретро слово градиент цвета искусства
1200*1200
bd письмо 3d круг логотип
1200*1200
в первоначальном письме bd шаблон векторный дизайн логотипа
1200*1200
Рождество 80 х годов ретро пиксель
9449*5315
Ретро ТВ игра 80 х годов в стиле арт дизайн
1200*1200
в первоначальном письме ба логотипа
1200*1200
Креативное письмо bb дизайн логотипа черно белый вектор минималистский
1202*1202
скейтборд в неоновых цветах 80 х
1200*1200
ТВ игра 80 х в стиле ретро
1200*1200
84 летие векторный дизайн шаблона иллюстрация
4083*4083
ТВ игра 80 х неоновый эффект слово дизайн
1200*1200
в эти выходные только мега продажи баннер скидки до 80 с
10418*10418
Ретро вечеринка 80 х годов цвет градиент искусства слово
1200*1200
ретро стиль 80 х годов диско дизайн неон плакат
5556*5556
мемфис образца 80 s 90 стилей на белом фоневектор иллюстрация
4167*4167
80 е в стиле ретро мода цвет градиент арт дизайн
1200*1200
80 основных форм силуэта
5000*5000
Построить линию — WebMath
Быстро! Мне нужна помощь с:
Выберите пункт справки по математике . .. Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степень комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesTheotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа с сложением, Вычитание числа Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с помощью GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
.. Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степень комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesTheotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа с сложением, Вычитание числа Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с помощью GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Что такое линейный график? — Определение, факты и пример
Что такое линейный график?
Линейный график — это тип диаграммы, используемый для отображения информации, которая изменяется во времени. Мы строим линейные графики, используя несколько точек, соединенных прямыми линиями. Мы также называем это линейным графиком. Линейный график состоит из двух осей, известных как ось «x» и ось «y».
Мы строим линейные графики, используя несколько точек, соединенных прямыми линиями. Мы также называем это линейным графиком. Линейный график состоит из двух осей, известных как ось «x» и ось «y».
- Горизонтальная ось называется осью x.
- Вертикальная ось называется осью Y.
На данном изображении описаны части линейного графика.
Название : сообщает о данных для каждого построенного линейного графика.
Ось x : сообщает о метках по оси x, которая обычно является временем.
Ось Y : сообщает о метках по оси Y, которые обычно представляют собой количество в числах
Тренд : Соединяем точки, чтобы нарисовать график. Точка пересечения метки на оси x и оси y говорит о тенденции. На данном рисунке пересечение в понедельник и 5 показывает, что в понедельник было продано 5 маффинов.
Построение линейного графика Построить линейный график очень просто. Вот простые шаги, которые следует учитывать при построении линейного графика.
Вот простые шаги, которые следует учитывать при построении линейного графика.
Начертите оси X и Y на миллиметровой бумаге. Обязательно напишите заголовок над таблицей, чтобы он определял назначение графика.
Например, если одним из факторов является время, он идет по горизонтальной оси, называемой осью x. Другой фактор впоследствии будет перемещаться по вертикальной оси, которая известна как ось y. Обозначьте обе оси в соответствии с их соответствующими коэффициентами.Например, мы можем обозначить ось x временем или днем.
После этого с помощью уже заданных данных укажите точные значения на графике. После того, как вы объедините точки, вы сможете сделать четкий вывод о тенденции.
Например, данный линейный график показывает тенденцию изменения температуры Нью-Йорка в жаркий день.
Чтение линейного графика Читать линейный график очень просто, и вы можете научиться читать график, прочитав приведенные ниже точки.
Во-первых, взгляните на две оси и попытайтесь понять, что обозначают эти оси.
Затем посмотрите на график и проверьте значения точек, расположенных на линиях графика.
Следуйте линиям и выясните, есть ли там подъем или падение. Также проверьте наличие повторяющихся узоров и пересечения линий. Таким образом, вы узнаете назначение линейного графика.
Также существует вероятность того, что вы в конечном итоге увидите появляющиеся модели, которые помогут вам угадать тренд.
Например: на приведенном выше графике максимальная температура была в 16:00, что составляло 55 градусов Цельсия. Прочтите приведенный выше график и ответьте на следующие вопросы:
A : О чем этот график?
B : Когда была минимальная температура?
C : Какая была температура в 15:00?
Интересные факты о линейном графике
|
Графические линии — Построение линейных уравнений | Линии | Склон
Темы
- Построение графиков линейных уравнений
- Линии
- Склон
Описание
Откройте для себя мир линий.Исследуйте взаимосвязь между линейными уравнениями, наклоном и графиками линий. Испытайте себя в линейной игре!
Примеры целей обучения
- Объясните, как можно вычислить наклон линии графика.
- Постройте прямую, заданную уравнением, в форме углового пересечения или точки-наклона.
- Напишите уравнение в форме точки наклона или точки наклона в виде линии графика.
- Спрогнозируйте, как изменение переменных в линейном уравнении повлияет на график.

Согласование стандартов
Общее ядро - математика
8.EE.B.5График пропорциональных соотношений, интерпретируя удельный вес как наклон графика. Сравните два разных пропорциональных отношения, представленных разными способами. Например, сравните график расстояние-время с уравнением расстояние-время, чтобы определить, какой из двух движущихся объектов имеет большую скорость.
8.EE.B.6Используйте похожие треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b .
8.EE.C.8a Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.
Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения. Разбирайте простые случаи путем осмотра. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не могут одновременно быть 5 и 6 .
8.F.A.3Интерпретируйте уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными. Например, функция A = s 2 , дающая площадь квадрата как функцию длины его стороны, не является линейной, потому что ее график содержит точки (1,1), (2,4) и (3,9 ), которые не находятся на прямой .
HSF-IF.C.7 Графические функции, выраженные символически и показывающие ключевые особенности графика, вручную в простых случаях и с использованием технологий для более сложных случаев. *
*
График линейных и квадратичных функций и отображение точек пересечения, максимумов и минимумов.
HSF-LE.A.1aДокажите, что линейные функции растут на равные разности через равные интервалы, а экспоненциальные функции растут на равные множители через равные интервалы.
Версия 1.3.10
HTML5 sims могут работать на iPad и Chromebook, а также на ПК, Mac и Linux.
iPad:
iOS 12+ Safari
iPad-совместимые sim-карты
Android:
Официально не поддерживается. Если вы используете симуляторы HTML5 на Android, мы рекомендуем использовать последнюю версию Google Chrome.
Chromebook:
Последняя версия Google Chrome
Симуляторы HTML5 и Flash PhET поддерживаются на всех устройствах Chromebook.
SIM-карты, совместимые с Chromebook
Системы Windows:
Microsoft Edge, последняя версия Firefox, последняя версия Google Chrome.
Системы Macintosh:
macOS 10.13+, Safari 13+, последняя версия Chrome.
Системы Linux:
Официально не поддерживается. Пожалуйста, свяжитесь с [email protected] по вопросам устранения неполадок.
Определение точек пересечения на графике линии
Результаты обучения
- Определите точки пересечения по оси x и y линии, представленные в форме уравнения
- Определить точки пересечения по оси x и y линии, представленной в виде графика
Каждое линейное уравнение имеет уникальную линию, которая представляет все решения уравнения.При построении линии путем нанесения точек каждый человек, который рисует линию, может выбрать любые три точки, поэтому два человека, рисующие линию, могут использовать разные наборы точек.
На первый взгляд, две их линии могут показаться разными, поскольку на них будут обозначены разные точки. Но если все работы были выполнены правильно, линии будут точно такими же. Один из способов узнать, что это действительно одна и та же линия, — это сосредоточиться на том, где линия пересекает оси. Каждая из этих точек называется точкой пересечения линии.
Один из способов узнать, что это действительно одна и та же линия, — это сосредоточиться на том, где линия пересекает оси. Каждая из этих точек называется точкой пересечения линии.
Перехват линии
Каждая из точек, в которых линия пересекает [latex] x \ text {-axis} [/ latex] и [latex] y \ text {-axis} [/ latex], называется точкой пересечения линии.
Давайте посмотрим на график, показанный ниже.
Сначала обратите внимание, где каждая из этих линий пересекает ось x -:
| Рисунок: | Линия пересекает ось x в точке: | Заказанная пара этой точки |
|---|---|---|
| [латекс] 42 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] (3,0) [/ латекс] |
| [латекс] 43 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] (4,0) [/ латекс] |
| [латекс] 44 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] (5,0) [/ латекс] |
| [латекс] 45 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] (0,0) [/ латекс] |
Вы видите узор?
Для каждой строки координата y- точки, в которой линия пересекает ось x- , равна нулю. Точка, в которой линия пересекает ось x- , имеет вид [латекс] \ left (a, 0 \ right) [/ latex]; и называется отрезком x линии. Перехват x- происходит, когда y равен нулю.
Точка, в которой линия пересекает ось x- , имеет вид [латекс] \ left (a, 0 \ right) [/ latex]; и называется отрезком x линии. Перехват x- происходит, когда y равен нулю.
Теперь давайте посмотрим на точки, в которых эти линии пересекают ось Y.
| Рисунок: | Линия пересекает ось Y в точке: | Заказываемая пара для этой точки |
|---|---|---|
| [латекс] 42 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] (0,6) [/ латекс] |
| [латекс] 43 [/ латекс] | [латекс] -3 [/ латекс] | [латекс] (0, -3) [/ латекс] |
| [латекс] 44 [/ латекс] | [латекс] -5 [/ латекс] | [латекс] (0, -5) [/ латекс] |
| [латекс] 45 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] (0,0) [/ латекс] |
[latex] x \ text {-intercept} [/ latex] — это точка [latex] \ left (a, 0 \ right) [/ latex], где график пересекает [латекс] x \ text {- ось} [/ латекс]. [Latex] x \ text {-intercept} [/ latex] возникает, когда [latex] \ text {y} [/ latex] равно нулю.
[Latex] x \ text {-intercept} [/ latex] возникает, когда [latex] \ text {y} [/ latex] равно нулю.
[latex] y \ text {-intercept} [/ latex] — это точка [latex] \ left (0, b \ right) [/ latex], где график пересекает [латекс] y \ text {- ось} [/ латекс].
[latex] y \ text {-intercept} [/ latex] возникает, когда [latex] \ text {x} [/ latex] равно нулю.
, пример
Найдите [латекс] x \ text {- и} y \ text {-intercepts} [/ latex] в каждой строке:
| 1. [латекс] x + 2y = 4 [/ латекс] | |
| 2.[латекс] 3x-y = 6 [/ латекс] | |
| 3. [латекс] x + y = -5 [/ латекс] |
Решение
| 1. | |
| График пересекает ось x в точке [latex] (4, 0) [/ latex]. | Перехват x — [латекс] (4, 0) [/ латекс]. |
| График пересекает ось y в точке [latex] (0, 2) [/ latex]. | Перехват x — [латекс] (0, 2) [/ латекс]. |
| 2. | |
| График пересекает ось x в точке [latex] (2, 0) [/ latex]. | Перехват x — [латекс] (2, 0) [/ латекс] |
| График пересекает ось y в точке [latex] (0, −6) [/ latex]. | Перехват y — [латекс] (0, -6) [/ латекс]. |
| 3. | |
| График пересекает ось x в точке [латекс] (- 5, 0) [/ латекс]. | Перехват x — [латекс] (- 5, 0) [/ латекс]. |
График пересекает ось y в точке [latex] (0, −5) [/ latex]. | Перехват y — [латекс] (0, -5) [/ латекс]. |
Признавая, что [latex] x \ text {-intercept} [/ latex] возникает, когда [latex] y [/ latex] равно нулю, и что [latex] y \ text {-intercept} [/ latex] возникает, когда [ latex] x [/ latex] равно нулю, дает нам метод найти точки пересечения линии из ее уравнения.Чтобы найти [latex] x \ text {-intercept,} [/ latex], пусть [latex] y = 0 [/ latex] и решит для [latex] x [/ latex]. Чтобы найти [latex] y \ text {-intercept} [/ latex], положите [latex] x = 0 [/ latex] и решите для [latex] y [/ latex].
Найдите
x и y из уравнения прямойВоспользуйтесь уравнением, чтобы найти:
пересечение линии x- , пусть [latex] y = 0 [/ latex] и решает для x .
пересечение линии y- , пусть [latex] x = 0 [/ latex] и решают относительно y .
| [латекс] x [/ латекс] | [латекс] y [/ латекс] |
|---|---|
| [латекс] 0 [/ латекс] | |
| [латекс] 0 [/ латекс] |
, пример
Найдите точки пересечения [латекса] 2x + y = 6 [/ latex]
Заполним таблицу ниже.
Чтобы найти точку пересечения с x, пусть [latex] y = 0 [/ latex]:
| [латекс] 2x + y = 6 [/ латекс] | |
| Заменить [латекс] 0 [/ латекс] на и . | [латекс] 2x + \ color {красный} {0} = 6 [/ латекс] |
| Доп. | [латекс] 2x = 6 [/ латекс] |
| Разделить на [латекс] 2 [/ латекс]. | [латекс] x = 3 [/ латекс] |
Перехват x — [латекс] (3, 0) [/ латекс]. |
Чтобы найти точку пересечения оси y, пусть [latex] x = 0 [/ latex]:
| [латекс] 2x + y = 6 [/ латекс] | |
| Замените [латекс] 0 [/ латекс] на x . | [латекс] 2 \ cdot \ color {красный} {0} + y = 6 [/ латекс] |
| Умножить. | [латекс] 0 + y = 6 [/ латекс] |
| Доп. | [латекс] y = 6 [/ латекс] |
| Перехват y — [латекс] (0, 6) [/ латекс]. |
точки пересечения — это точки [латекс] \ влево (3,0 \ вправо) [/ латекс] и [латекс] \ влево (0,6 \ вправо) [/ латекс].
, пример
Найдите точки пересечения [latex] 4x — 3y = 12 [/ latex].
Показать решение Решение
Чтобы найти [латекс] x \ text {-intercept,} [/ latex], пусть [latex] y = 0 [/ latex].
| [латекс] 4x — 3y = 12 [/ латекс] | |
| Замените [латекс] 0 [/ латекс] на [латекс] y [/ латекс]. | [латекс] 4x — 3 \ cdot 0 = 12 [/ латекс] |
| Умножить. | [латекс] 4x — 0 = 12 [/ латекс] |
| Вычесть. | [латекс] 4x = 12 [/ латекс] |
| Разделить на [латекс] 4 [/ латекс]. | [латекс] x = 3 [/ латекс] |
[латекс] x \ text {-intercept} [/ latex] — это [latex] \ left (3,0 \ right) [/ latex].
Чтобы найти [латекс] y \ text {-intercept} [/ latex], пусть [latex] x = 0 [/ latex].
| [латекс] 4x — 3y = 12 [/ латекс] | |
| Замените [латекс] 0 [/ латекс] на [латекс] x [/ латекс]. | [латекс] 4 \ cdot 0 — 3y = 12 [/ латекс] |
| Умножить. | [латекс] 0 — 3y = 12 [/ латекс] |
Упростить. | [латекс] -3y = 12 [/ латекс] |
| Разделить на [латекс] −3 [/ латекс]. | [латекс] y = -4 [/ латекс] |
[latex] y \ text {-intercept} [/ latex] — это [latex] \ left (0, -4 \ right) [/ latex].
Перехваты — это точки [латекс] \ влево (-3,0 \ вправо) [/ латекс] и [латекс] \ влево (0, -4 \ вправо) [/ латекс].
| [латекс] 4x — 3y = 12 [/ латекс] | |
|---|---|
| x | y |
| [латекс] 3 [/ латекс] | [латекс] 0 [/ латекс] |
| [латекс] 0 [/ латекс] | [латекс] -4 [/ латекс] |
Графические линейные уравнения
График линейного уравнения с двумя переменными представляет собой линию (поэтому его называют линейный ).
Если вы знаете, что уравнение линейно, вы можете построить его график, найдя любые два решения.
( Икс 1 , у 1 ) и ( Икс 2 , у 2 ) ,
нанести эти две точки на карту и провести линию, соединяющую их.
Пример 1:
Изобразите уравнение Икс + 2 у знак равно 7 .
Вы можете найти два решения, соответствующие Икс -перехватывает и у -перехватывает графика, установив сначала Икс знак равно 0 а потом у знак равно 0 .
Когда Икс знак равно 0 , мы получили:
0
+
2
у
знак равно
7
у
знак равно
3. 5
5
Когда у знак равно 0 , мы получили:
Икс + 2 ( 0 ) знак равно 7 Икс знак равно 7
Итак, две точки ( 0 , 3.5 ) и ( 7 , 0 ) .
Постройте эти две точки и проведите линию, соединяющую их.
Если уравнение находится в форма пересечения склонов или же точечно-наклонная форма , вы также можете использовать склон чтобы помочь вам построить график.
Пример 2:
Постройте линию у знак равно 3 Икс + 1 .
Из уравнения мы знаем, что
у
-перехват
1
, смысл
(
0
,
1
)
и наклон
3
. Постройте точку
(
0
,
1
)
и оттуда идти вверх
3
единиц и вправо
1
единицы и нанесите на график вторую точку. Проведите линию, содержащую обе точки.
Постройте точку
(
0
,
1
)
и оттуда идти вверх
3
единиц и вправо
1
единицы и нанесите на график вторую точку. Проведите линию, содержащую обе точки.
Горизонтальные и вертикальные линии иметь очень простые уравнения.
Пример 3:
Горизонтальная линия: у знак равно 3
Вертикальная линия: Икс знак равно — 2
Линейный график— все, что вам нужно знать о линейных графиках
Что такое линейный график?
Линейный график, также известный как линейная диаграмма, представляет собой тип диаграммы, используемый для визуализации значения чего-либо с течением времени.Например, финансовый отдел может построить график изменения суммы наличных денег, имеющихся в наличии у компании, с течением времени.
Линейный график состоит из горизонтальной оси x и вертикальной оси y. Большинство линейных графиков имеют дело только с положительными числовыми значениями, поэтому эти оси обычно пересекаются около нижней части оси y и левого конца оси x. Точка пересечения осей всегда (0, 0). Каждая ось помечена типом данных. Например, по оси X могут быть дни, недели, кварталы или годы, а по оси Y — доход в долларах.
Точки данных нанесены на график и соединены линией «точка-точка».
Ось x также называется независимой осью, потому что ее значения ни от чего не зависят. Например, время всегда помещается на ось x, поскольку оно продолжает двигаться вперед независимо от чего-либо еще. Ось Y также называется зависимой осью, потому что ее значения зависят от значений оси X: в то время у компании было столько денег. В результате линия графика всегда движется горизонтально, и каждое значение x имеет только одно значение y (компания не может иметь две суммы денег одновременно).
Более одной линии могут быть нанесены на одну ось в качестве формы сравнения. Например, вы можете создать линейный график, сравнивающий сумму денег, хранящуюся в каждом филиале, с отдельной строкой для каждого офиса. В этом случае каждая линия будет иметь свой цвет, обозначенный в легенде.
Например, вы можете создать линейный график, сравнивающий сумму денег, хранящуюся в каждом филиале, с отдельной строкой для каждого офиса. В этом случае каждая линия будет иметь свой цвет, обозначенный в легенде.
Линейный график — это мощный визуальный инструмент для маркетинга, финансов и других областей. Это также полезно в лабораторных исследованиях, мониторинге погоды или любой другой функции, связанной с корреляцией между двумя числовыми значениями.Если на графике есть две или более линий, это можно использовать для сравнения между ними.
Как создать линейный график
Шаг первый — убедиться, что данные правильно отформатированы для линейного графика.
На вкладке Insert в SmartDraw щелкните Graph и выберите Line Graph. .
Выберите файл данных для импорта, и SmartDraw автоматически сгенерирует график.
После импорта вы можете легко изменить заголовок, размещение легенды и даже быстро изменить тип графика с помощью параметров Edit Graph или просто дважды щелкнув импортированную диаграмму.
— определение и простые шаги для создания одного
Определения статистики> Линейный график
Что такое линейный график?
Линейный график показывает, как меняются значения. Например, вы можете изобразить, как ваш ребенок растет с течением времени. Линейные графики также можно использовать, чтобы показать, как меняются функции. Функция — это просто уравнение, которое дает вам уникальный результат для каждого входа. Например, y = — 4 / 5x + 3 — это функция, потому что вы получите уникальное значение для y, если введете любое число для x.
Самый обычный тип данных, который вы найдете на линейном графике, — это , как что-то меняется с течением времени . Линейный график, который показывает изменения во времени, иногда называют временным графиком.
График Доу-Джонса из Wall Street Journal показывает, как фондовый рынок меняется с течением времени.
Линейные графики имеют горизонтальную ось (ось x) и вертикальную ось (ось y). В большинстве случаев время откладывается по горизонтальной оси.
В большинстве случаев время откладывается по горизонтальной оси.
Зачем нужен линейный график?
Линейный график имеет характеристики, которые делают его полезным в некоторых ситуациях.Вы бы использовали линейный график, если:
- У вас есть функция . Линейные графики хорошо показывают определенные значения данных, а это означает, что если у вас есть одна переменная (x), вы можете легко найти другую (y).
- Вы хотите показать тенденции. Например, как ваши инвестиции меняются с течением времени или как с течением времени росли цены на продукты питания.
- Вы хотите делать прогнозы. Линейный график можно экстраполировать за пределы имеющихся данных. Они позволяют вам делать прогнозы относительно результатов данных.
Части линейного графика.
| Название | Сообщает вам, о чем график. |
| Этикетки осей | Сообщает вам, какие данные находятся на каждой оси. |
| Масштаб оси | Показывает, сколько или сколько данных находится на каждой оси. |
| Очки | Дает вам конкретную точку данных на линейном графике со значениями x и y. |
| Строки | Дает вам оценку значений между точками для дискретных функций (дискретные функции состоят из точек данных).В непрерывных функциях линия дает вам фактических данных , а не оценку. |
Как построить линейный график
Линейные графики очень легко построить на миллиметровой бумаге.
Первый шаг: нарисуйте линию для оси x и оси y.
Второй шаг: добавьте метки осей и масштаб оси.
Третий шаг: после этого отметьте точки данных.
Четвертый шаг: Затем проведите линию через точки данных.
Пятый шаг: наконец, добавьте заголовок диаграммы.
Проблемы с линейными графиками.
Линейные графики могут вводить в заблуждение. Например, на этом графике показаны данные о продажах за 4 дня. Что с этим не так?
Что с этим не так?
График вводит в заблуждение из-за неровного масштаба по оси y. Создается впечатление, что между 1 и 2 днями (8) произошел огромный скачок продаж, тогда как на самом деле был больший скачок между 3 и 4 (11).
А как насчет этого реального графика температур в Нью-Хейвене, Коннектикут? Это ясно показывает, что происходит глобальное потепление.
Изображение: Йельский университет
Если присмотреться, вы увидите, что температуры отображаются только для первой половины года.Это обычная тактика введения зрителей в заблуждение.
Должен ли линейный график начинаться с начала координат?
График, который начинается с нуля, легче понять и прочитать. Однако, в отличие от гистограмм, для линейных графиков нет установленного правила, согласно которому вы должны начинать с начала координат. С учетом сказанного, если вы решите начать с числа, отличного от нуля, будьте осторожны, чтобы не преувеличивать бессмысленные небольшие различия (см. Вводящие в заблуждение графики для некоторых примеров), например, этот из Fox News:
Вводящие в заблуждение графики для некоторых примеров), например, этот из Fox News:
Этот график намеренно начат с 8%, чтобы иметь очень небольшую разницу (.2%) выглядят крупными. Источник изображения: http://cloudfront.mediamatters.org
После этого скачок на 0,2% может быть очень значимым в некоторых обстоятельствах, например, рост числа излечимых болезней. В общем, вы можете начать ось с того места, где захотите — только будьте осторожны, чтобы не ввести читателя в заблуждение.
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

 Заголовок записывается в небольшом поле ввода. Чтобы определить местонахождение заголовка графика надо снова открыть вкладку «Работа с диаграммами», после чего выбрать «Макет» и «Название диаграммы». Всплывет перечень возможных расположений заголовка.
Заголовок записывается в небольшом поле ввода. Чтобы определить местонахождение заголовка графика надо снова открыть вкладку «Работа с диаграммами», после чего выбрать «Макет» и «Название диаграммы». Всплывет перечень возможных расположений заголовка.  Самое оптимальное значение – 1. Если наблюдаются отклонения, это говорит о степени достоверности построенной статистической модели.
Самое оптимальное значение – 1. Если наблюдаются отклонения, это говорит о степени достоверности построенной статистической модели.  Чтобы это сделать, нужно воспользоваться пунктом «Изменить тип диаграммы».
Чтобы это сделать, нужно воспользоваться пунктом «Изменить тип диаграммы». Другой вариант: нажмите кнопку Добавить элемент диаграммы (Add Chart Elements), которая находится в разделе Макеты диаграмм (Chart Layouts) на вкладке Конструктор (Design).
Другой вариант: нажмите кнопку Добавить элемент диаграммы (Add Chart Elements), которая находится в разделе Макеты диаграмм (Chart Layouts) на вкладке Конструктор (Design). Установите такое количество точек, которое, по Вашему мнению, будет оптимальным. Например, если Вы считаете, что определённая тенденция в данных сохраняется неизменной только для последних 4 точек, то введите число 4 в данном поле.
Установите такое количество точек, которое, по Вашему мнению, будет оптимальным. Например, если Вы считаете, что определённая тенденция в данных сохраняется неизменной только для последних 4 точек, то введите число 4 в данном поле. Вертикальные линии пересекают ряд групповых и детальных сечений. Crystal reports-это версия 13, и я использую ее в конструкторе в Visual Studio 2013. У меня две проблемы 1)…
Вертикальные линии пересекают ряд групповых и детальных сечений. Crystal reports-это версия 13, и я использую ее в конструкторе в Visual Studio 2013. У меня две проблемы 1)… Try making it a vector as follows:
...
PiE = []
j = 1;
Dt=[(Vmax/A1)-(Vmax/A0)]+[((Vlow-Vmin)+(Vmax-Vhigh))/A1]+[((Vmax-Vhigh)+(Vlow-
Vmin))/A0];
for i=-x:0.1:x
DPiI=PiD+[PiC*(Vhigh/A1)]+PiP*i+PiC*i;
PiE(j)=DPiI/Dt;
j=j+1;
end
plot (x,PiE)
Try making it a vector as follows:
...
PiE = []
j = 1;
Dt=[(Vmax/A1)-(Vmax/A0)]+[((Vlow-Vmin)+(Vmax-Vhigh))/A1]+[((Vmax-Vhigh)+(Vlow-
Vmin))/A0];
for i=-x:0.1:x
DPiI=PiD+[PiC*(Vhigh/A1)]+PiP*i+PiC*i;
PiE(j)=DPiI/Dt;
j=j+1;
end
plot (x,PiE)
 Пока что я рисую вертикальный прямоугольник поверх своего графика в тех местах, где, по моим расчетам, он пересекается. Он работает…
Пока что я рисую вертикальный прямоугольник поверх своего графика в тех местах, где, по моим расчетам, он пересекается. Он работает…
 Кроме того, можно
попробовать расположить их в порядке,
соответствующем полученному уравнению множественной регрессии, факторным
нагрузкам или объясняемым факторам (см. главу Факторный анализ). Таким образом
можно упростить и сделать более
«однородным» общий вид пиктограмм, чтобы
легче идентифицировать слабо выраженные
различия. В то же время такой подход может
затруднить идентификацию некоторых структур. На
этом этапе можно дать только один универсальный
совет: прежде чем использовать какие-либо
сложные методы, попробуйте наиболее простой и
быстрый вариант, а именно, случайную
последовательность переменных.
Кроме того, можно
попробовать расположить их в порядке,
соответствующем полученному уравнению множественной регрессии, факторным
нагрузкам или объясняемым факторам (см. главу Факторный анализ). Таким образом
можно упростить и сделать более
«однородным» общий вид пиктограмм, чтобы
легче идентифицировать слабо выраженные
различия. В то же время такой подход может
затруднить идентификацию некоторых структур. На
этом этапе можно дать только один универсальный
совет: прежде чем использовать какие-либо
сложные методы, попробуйте наиболее простой и
быстрый вариант, а именно, случайную
последовательность переменных. На этом этапе
лучше использовать пиктографики кругового
типа.
На этом этапе
лучше использовать пиктографики кругового
типа.

