Рисунок из геометрических фигур 5 класс: Творческая работа учащихся (5 класс) по теме: Презентация «Рисунки из геометрических фигур», ученица 5а класса школы надомного обучения №367 Гусева Анастасия
Творческая работа учащихся (5 класс) по теме: Презентация «Рисунки из геометрических фигур», ученица 5а класса школы надомного обучения №367 Гусева Анастасия
Слайд 1
Автор презентации: Гусева Анастасия Класс 5-б Руководитель: Монакова К.З. Москва 2010 г. ГОУ СОШ «Школа надомного обучения» 367 Зеленоградского округа г. Москвы Конкурс «Умники и умницы» «Рисунки из геометрических фигур» (математика)Слайд 2
1. Компьютерная графика. 2.Геометрические игры – головоломки: «Пифагор», «Архимед», « Танграм » и др. 3. Рисунки по координатам. Геометрический зоопарк. 3. «Живая геометрия» Рисунки из геометрических фигур . . Содержание:
Слайд 3
Знаменитые старинные головоломки из геометрических фигур: «Пифагор», «Архимед», « Тагнрам » и другие …
Слайд 4
Развивает умственные и творческие способности детей. Суть игры заключается в конструировании на плоскости разнообразных предметных силуэтов, напоминающих животных, людей, предметы быта, транспорт, буквы, цифры, цветы и т. д. В каждой модели используются все семь фигур «Квадрата Пифагора». Благодаря сложности и многообразию геометрических фигур, игра развивает пространственное воображение, комбинаторные способности, сообразительность, смекалку, усидчивость. Головоломка «Пифагора» — это к вадрат размером 7х7 см , разрезанный на 7 частей. Из полученных фигур можно сложить различные силуэты. Головоломка «Пифагор»
д. В каждой модели используются все семь фигур «Квадрата Пифагора». Благодаря сложности и многообразию геометрических фигур, игра развивает пространственное воображение, комбинаторные способности, сообразительность, смекалку, усидчивость. Головоломка «Пифагора» — это к вадрат размером 7х7 см , разрезанный на 7 частей. Из полученных фигур можно сложить различные силуэты. Головоломка «Пифагор»
Слайд 5
Простейшие фигурки из деталей «Квадратов Пифагора»
Слайд 6
Головоломка Архимеда « Стомахион » (приводящая в ярость) Игра была известна еще до нашей эры. Создателем ее считали Архимеда, в нее играли еще в глубокой древности. Чтобы сделать такую игру, надо взять прямоугольник одна сторона которого в 2 раза больше другой. Элементы игры получаются путем произвольного деления прямоугольника на 14 частей. Из получившихся деталей конструируют на плоскости разнообразные предметные силуэты, например, сидящей собаки, бегущего человека, разнообразных цветов, птиц. Можно сложить и многофигурные композиции.
Слайд 7
Головоломка «Сфинкс» . В ее состав входит 7 простых геометрических фигур: 4 треугольника и 3 четырехугольника с разным соотношением сторон.
Слайд 8
Геометрия Головоломки «Архимеда»
Слайд 9
И еще…
Слайд 10
«Геометрическая семья»
Слайд 11
Геометрический подарок к празднику
Слайд 12
Геометрический тренинг
Слайд 13
1 2 3 6 4 5 7 Детали « Танграма ». Квадрат разделен на 7 кусков как показано на рисунке: 5 различных треугольников, квадрат и параллелограмм .
Слайд 14
Более сложные рисунки из 7 частей « Танграма »: дом, машина, лошадь, мальчик на ослике; человек, толкающий тачку; собака, велосипедист, британский лев и др .
Слайд 15
Рисунки по координатам ГЕОМЕТРИЧЕСКИЙ ЗООПАРК. 1 Рисунок по координатам «Верблюд».
Слайд 16
2 Рисунок по координатам «СТРАУС »
Слайд 17
3 Рисунок по координатам «Лебедь»
Слайд 18
4 Рисунок по координатам «ЛИС»
Слайд 19
Рисунок 1 «Медвежонок» выполнен в программе «Живая геометрия»
Слайд 20
Рисунок 2 из геометрических фигур «Живая геометрия»
Слайд 21
1. Материалы сети Интернет. 2. «520 головоломок». Генри Э.Дьюдени . 3. Наглядная геометрия. И.Ф.Шарыгин . 4. Очерки о математических задачах на смекалку. Б.А.Кордемский . 5. Практикум по компьютерной технологии. О.Ефимова, В. Морозов. 6. Увлекательная математика. И.Леман . И др. Литература:
Материалы сети Интернет. 2. «520 головоломок». Генри Э.Дьюдени . 3. Наглядная геометрия. И.Ф.Шарыгин . 4. Очерки о математических задачах на смекалку. Б.А.Кордемский . 5. Практикум по компьютерной технологии. О.Ефимова, В. Морозов. 6. Увлекательная математика. И.Леман . И др. Литература:
Проект (5 класс) на тему: Конкурс творческих проектов «Фантазии с геометрическими фигурами» в рамках кружка «В мире математики»
Слайд 1
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ Работу выполнила ученица 5 «В» класса МКОУ Таловской СОШ Зеленина ИринаСлайд 2
ТРЕУГОЛЬНИК Самолёт летит по небу- треугольное крыло, на моём велосипеде — треугольное седло. Есть такой предмет угольник, и всё это – ТРЕУГОЛЬНИК.
Слайд 3
КВАДРАТ Доска, где шахматы стоят, и клетка каждая – квадрат. Стоят там кони и слоны, фигуры боевые. КВАДРАТ – четыре стороны, все стороны его равны, и все углы прямые.
Слайд 4
КРУГ КРУГ — тарелка, колесо, ОКРУЖНОСТЬ — обруч, поясок.
Слайд 5
ОВАЛ А как нарисовать овал? На помощь брата я позвал. Брат взял фломастер и искусно мне овал нарисовал: ты слегка окружность сплюсни, получается ОВАЛ.
Брат взял фломастер и искусно мне овал нарисовал: ты слегка окружность сплюсни, получается ОВАЛ.
Слайд 6
Конус Сказала мама: «А сейчас про конус будет мой рассказ. В высокой шапке звездочёт считает звёзды круглый год. КОНУС- шляпа звездочёта. Вот какой он. Понял? То-то».
Слайд 7
КУБ Принёс нам ящик почтальон — посылка мне и брату. Ящик — КУБ, в нём шесть сторон, все стороны — квадраты. А что лежит в посылке? Там стружки и опилки, конфеты и баранки, ещё с вареньем банки.
Слайд 8
ТОЧКА Пуст сегодня дворик наш, за окошком хмуро. Я взял фломастер, карандаш, решил чертить фигуры. Передо мной бумаги лист. До чего ж он бел и чист. Фломастером ткнёшь посредине листочка, и на листе получается … .
Слайд 9
ПИРАМИДА Я видел картину. На этой картине стоит ПИРАМИДА в песчаной пустыне. Всё в пирамиде необычайно. Какая-то есть в ней загадка и тайна. А Спасская башня на площади Красной и детям, и взрослым знакома прекрасно. Посмотришь на башню — обычная с виду. А что на вершине у ней? — Пирамида.
А что на вершине у ней? — Пирамида.
Слайд 10
ПРЯМАЯ ЛИНИЯ Мне посоветовала мама Вести свою дорогу прямо. Как сделать линию прямой? Никак не получается. Фломастер у меня хромой Или рука сбивается? А вот с линейкой по листу Так просто провести черту. Смотрите, ровная какая — Это линия — ПРЯМАЯ.
Слайд 11
ШАР Удар! Удар! Ещё удар! Летит в ворота мячик — ШАР! А это — шар арбузный, зелёный, круглый, вкусный. Вглядитесь лучше – шар каков ! Он сделан из одних кругов. Разрежьте на круги арбуз И их попробуйте на вкус.
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Геометрические фигуры 1 класс — Онлайн-тренажер
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
1. Рисунки из геометрических фигур — Условия к выполнению заданий:
Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.
- В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры.
 Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки. - Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).
Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.
2. Геометрические фигуры в рисунках — 3 задания-раскраски:
Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.
Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.
3. Развивающая раскраска для детей — Смешные рисунки из фигур
В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.
Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.
Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Счет до 10 для дошкольников
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Геометрические фигуры из бумаги — Вырезаем и занимаемся!
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.
Объемные геометрические фигуры из бумаги — Вырезаем и клеим:
Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Скачать геометрические фигуры из бумаги — развертки для вырезания вы можете во вложениях внизу страницы
Лист 1
Лист 2
Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.
Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: «Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:
Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)
Что такое куб:
Что такое конус и цилиндр. На что они похожи:
Можете также скачать эти обучающие картинки во вложениях.
Плоские геометрические фигуры из бумаги — Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
«Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.
Карточка 1
Карточка 2
Карточка 3
Карточка 4
Карточка 5
Карточка 6
Геометрические фигуры для вырезания:
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Счет до 10 для детей дошкольного возраста
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Плоские геометрические фигуры — Обведи и дорисуй!
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги. Поэтому очень важно начинать обучение малышей с таких развивающих заданий, которые мы собрали для вас на этой странице.
Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги. Поэтому очень важно начинать обучение малышей с таких развивающих заданий, которые мы собрали для вас на этой странице.
1. Плоские геометрические фигуры — Обведи, дорисуй и раскрась:
В этом развивающем уроке ребенок встретит два задания, с помощью которых он научится рисовать плоские геометрические фигуры: раскрашивание фигур определенным образом и обведение фигур по пунктирной линии, а затем дорисовке отсутствующей части.
- В первом задании малыш с помощью пространственного мышления должен расположить (т. е. раскрасить) фигуры таким образом, чтобы каждая из них либо накрывала соседнюю, либо оказывалась под ней. Итак, условие к заданию: квадрат накрыл один угол треугольника, овал оказался на прямоугольнике, а треугольник разместился под кругом. Как вы уже догадались, для того, чтобы получилась такая картина, нужно соприкасающиеся фигуры раскрашивать в разные цвета.

- Во втором задании ребенку предстоит обвести пунктирные линии, определить в процессе форму обводимой фигуры и дорисовать самостоятельно ее недостающую часть. После этого фигуры можно раскрасить в произвольные цвета.
Чтобы объяснить ребенку, какие отличия имеют плоские геометрические фигуры и объемные, можете дополнить занятие следующим примером. Из листа обычной бумаги вырежьте квадрат и дайте ребенку, чтобы он оценил его поверхность и объем. Пусть малыш ощутит его в руках, затем положит на стол и посмотрит на фигуру со всех сторон. Скажите ему, что квадрат, который он держит в руках — плоский. После этого возьмите обычный детский кубик и, дав ребенку, скажите, что этот предмет также является квадратом, только теперь он объемный. Дайте ему пощупать кубик, покрутить в руках и посмотреть на него со всех сторон. Не нужно больше ничего говорить и тем более что-то объяснять и разжевывать.
Скачать задание — Плоские геометрические фигуры вы можете во вложениях.
2. Простые геометрические фигуры карандашом — Обведи по точкам
Обводить рисунки по точкам — чрезвычайно интересное занятие для детей. Используя этот детский интерес можно научить их рисовать простые геометрические фигуры, а заодно и потренировать воображение. Ведь в этом задании малыш должен в уме представить, какие точки нужно соединить между собой, чтобы получилась заданная фигура. Данное задание также формирует полезный для школы навык — умение ориентироваться на образец и заданные требования.
Задания необходимо выполнять карандашом, чтобы можно было в процессе работы стереть ластиком ненужные линии. Ведь ребенок будет ошибаться и это абсолютно нормально. Помните, «не ошибается тот, кто ничего не делает».
Вам нужно скачать 2 бланка с простыми геометрическими фигурами. На каждом бланке дается по 3 задания. В 1 и 5 задании нужно нарисовать по образцу неправильные треугольники, во 2 задании — неправильную трапецию, в 3 задании — ромб, в 4 задании — соединить по точкам квадрат, а в 6 задании — четырех лучевую звезду.
Как проводить занятие. Взрослый дает ребенку рассмотреть первое задание и указывая на три вершины треугольника говорит: «Видишь, сначала здесь были точки, которые соединили между собой таким образом, что получился этот рисунок (взрослый указывает на стороны треугольника, но не произносит слов «треугольник», «вершина», «стороны»). А вот здесь (и показывает на точки рядом с треугольником) нарисованы точки, из которых тебе следует выбрать такие, соединив которые получится точно такой рисунок. Но будь внимателен, так как здесь есть лишние точки — их соединять не нужно. Ты сам должен решить, какие точки лишние.»
Затем взрослый предлагает ребенку рассмотреть нарисованные точки и спрашивает у него «Все ли точки одинаковые?» Когда ребенок ответит «Нет», взрослый, подтвердив его ответ, объясняет ребенку условия соединения точек: «Все точки разные. Здесь есть белые точки, черные и с крестиком внутри. Ты должен запомнить правила: одинаковые точки нельзя соединять между собой, нельзя проводить линию от белой точки к белой, от черной — к черной, от точки с крестиком — к точке с крестиком. То есть соединять между собой можно только разные точки. Запомнил? Теперь можешь приступать к выполнению заданий.»
То есть соединять между собой можно только разные точки. Запомнил? Теперь можешь приступать к выполнению заданий.»
Скачать задание «Простые геометрические фигуры карандашом — Обведи по точкам» вы можете во вложениях внизу страницы.
3. Дорисуй фигуру по образцу — Геометрия для малышей
Еще одно развивающее занятие по рисованию и запоминанию геометрических фигур — Дорисуй фигуру по образцу. Здесь ребенок должен дорисовать недостающие элементы в каждой фигуре, руководствуясь бланком с готовыми фигурами. Для занятия необходимы: карандаш, ластик, линейка, 4 распечатанных бланка заданий.
Прежде чем приступить к выполнению упражнения, объясните ребенку правила, по которым он должен действовать:
- В первом задании (бланки №1 и №2) ребенку сначала нужно внимательно рассмотреть бланк №1 с готовыми геометрическими фигурами. Затем спросите его, какие фигуры из нарисованных ему знакомы. Подскажите ребенку название тех фигур, которые он не сможет назвать.
 Когда с фигурами станет все предельно ясно — дайте ребенку бланк №2 с недостающими деталями и скажите ему, что на этом листе геометрические фигуры немного испортились. И теперь его задача — исправить их для получения точно такого результата, как на бланке №1.
Когда с фигурами станет все предельно ясно — дайте ребенку бланк №2 с недостающими деталями и скажите ему, что на этом листе геометрические фигуры немного испортились. И теперь его задача — исправить их для получения точно такого результата, как на бланке №1. - Во втором задании (бланки №3 и №4) упражнение проводится аналогично предыдущему. Только в отличие от первого задания, здесь ребенку нужно не только дорисовать фигуры, но и дораскрасить, ориентируясь на образец.
Фигуры с прямыми линиями легче дорисовать с помощью линейки. Если ребенок еще не умеет ей пользоваться, то взрослый должен показать ему, как это делать.
Скачать задания «Дорисуй фигуру по образцу» вы можете во вложениях внизу страницы.
Бланк №1 — Готовые фигуры для 1 задания
Бланк №2 — Фигуры с недостающими деталями для 1 задания
Бланк №3 — Готовые фигуры для 2 задания
Бланк №4 — Фигуры с недостающими частями для 2 задания
4. Упражнение «Найди геометрические фигуры»
Упражнение «Найди геометрические фигуры»
Здесь вы можете скачать и распечатать бланк с заданием — Найди геометрические фигуры — для занятий с ребенком или с группой детей. Такие упражнения очень важны для развития логико-математических способностей в процессе обучения (или подготовке к обучению) начальных азов геометрии.
Распечатанный бланк с заданием нужно дать ребенку и попросить его внимательно рассмотреть изображение и найти в нем 1 четырехугольник и 5 треугольников.
Скачать задание «Найди геометрические фигуры» вы можете во вложениях внизу страницы
Чтобы продолжить изучать с ребенком геометрию, можете скачать геометрические фигуры для вырезания из бумаги, распечатать, вырезать и использовать как дополнительный обучающий материал.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Чтобы продолжить изучать с ребенком геометрию, можете скачать геометрические фигуры для вырезания из бумаги, распечатать, вырезать и использовать как дополнительный обучающий материал.
Счет до 5 — Картинки с заданиями для малышей
Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Животные из геометрических фигур: картинки для детей
Умеете ли вы составлять животных из геометрических фигур?
Никогда не пробовали?
Тогда стоит посмотреть картинки на сайте, где из геометрических фигур сложены разнообразные животные. Предложите эти рисунки своим детям: наверняка они оценят их оригинальность.
Геометрический мир
Во всем, что нас окружает, можно отыскать элементы геометрии.
Стол может быть круглым или квадратным, наши дома – параллелепипеды и т.д. Не наблюдали, как рисуют художники? Они сначала намечают контуры предмета с основой из геометрических фигур, а уж затем проводят вокруг них плавные линии. Они видят мир геометрическим, а ровные или мягкие линии лишь скрывают настоящую суть вещей.
Они видят мир геометрическим, а ровные или мягкие линии лишь скрывают настоящую суть вещей.
В педагогике для детей дошкольного возраста есть даже целое направление, где ребят учат во всем видеть чистые геометрические фигуры. Это педагогика Марии Монтессори. Она считала, что чистые геометрические фигуры способствуют лучшему развитию детей и их ориентации в мире. Нельзя сказать, что эта система идеальна, но она нашла своих сторонников.
А теперь давайте вспомним произведения художников эпохи модернизма и постмодернизма. Перед глазами встают картины, наполненные квадратами, треугольниками, кругами, трапециями и всевозможными фигурами, окрашенными в разные цвета. Так живописцы новой эпохи видели мир, и этому должно было основание. Они пытались передать этот мир нетронутым человеческими руками. Их стремлением было показать, что все мы и все предметы вокруг нас состоят из геометрических фигур. Весь наш мир, если присмотреться, — сплошная геометрия.
Как использовать картинки в работе с детьми
Вполне понятно, что встает вопрос: одно дело художники, но зачем детям такое видение мира?
Конечно, картинки с животными из геометрических фигур не ставят целью навязать малышу неординарное видение мира. Однако почему бы ни показать, что и такая трактовка всего, что нас окружает, возможна.
Однако почему бы ни показать, что и такая трактовка всего, что нас окружает, возможна.
По картинкам можно интересно и увлекательно изучать названия геометрических фигур. От простого показа и повторения ребенок быстро устает и начинает отказываться от занятий, даже если их проводит мама в домашних условиях. Другое дело, если фигуры необходимо отыскать в животных. Тут просыпается неподдельное любопытство.
Когда вы полностью изучите с ребенком названия фигур и их внешний вид, попросите ребенка проявить свое видение мира. Пусть для примера будет взято животное или любой предмет.
Спросите: на какую геометрическую фигуру он похож.
Такие упражнения:
- — развивают наблюдательность;
- — совершенствуют логическое и пространственное мышление;
- — способствуют видению скрытого за внешней оболочкой предмета.
Малыш учится видеть и наблюдать то, что не могут или не умеют видеть другие. Это ли не воспитание художника и творческой личности?
А можно поиграть в обратную игру. Представьте, что вы художники-абстракционисты. Пусть один из вас нарисует что-нибудь, состоящее из геометрических фигур, а другой попытается отгадать, что нарисовано. Живописцы постмодернизма часто зашифровывали свои рисунки на полотне, заполненной квадратами, прямоугольниками, трапециями… такие же головоломки предлагали ранее детские журналы.
Представьте, что вы художники-абстракционисты. Пусть один из вас нарисует что-нибудь, состоящее из геометрических фигур, а другой попытается отгадать, что нарисовано. Живописцы постмодернизма часто зашифровывали свои рисунки на полотне, заполненной квадратами, прямоугольниками, трапециями… такие же головоломки предлагали ранее детские журналы.
Вы и сами можете создать такую головоломку: нужно лишь немного фантазии и взгляд на мир сквозь призму геометрии.
Бесплатные ссылки на пособия с аппликациями:
Нажмите на картинку, чтобы скачать эту тетрадку с заданиями для детей бесплатно.Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет. Аппликации для детей от 4 до 7 лет. Нажмите на картинку, чтобы скачать эту книгу.| Загадка Ферма и тройки Пифагора | ||||||||||||||||||||||||||||||||||||||||
Теорема Пифагора утверждает, что для прямоугольного треугольника с катетами a и b и гипотенузой
c,  Числа, соответствующие этому шаблону, называются тройками Пифагора. На диаграмме ниже показаны некоторые из этих троек Пифагора. Изучите шаблон в диаграмму, чтобы найти следующие два набора троек. | ||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||
| Будет ли какая-либо из троек удовлетворять Великой теореме Ферма — a 3 + b 3 = c 3 ? А как насчет a 4 + b 4 = c 4 ? Следующие формулы можно использовать для генерации чисел, удовлетворяющих Теорема Пифагора.Убедитесь, что x> y и что один из них нечетный, а другой даже. a = x 2 — y 2 b = 2xy c = x 2 + y 2 Вот пример: пусть x = 7 и y = 6.
Совет: чтобы получить числа a, b и c, не имеющие общих делителей, убедитесь, что ваши числа x и y не имеют общих делителей, например 5 и 6 или 5 и 8, но не 5 и 10. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Шарлин Эванс | ||||||||||||||||||||||||||||||||||||||||
Ссылка: Коллинз, Уильям и др. Математика: приложения и связи,
Курс 3. | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | ||||||||||||||||||||||||||||||||||||||||
| Волшебный круг | ||||||||||||||||||||||||||||||||||||||||
Материалы
Предложите учащимся решить три задачи, которые имеют значение только для диаметра. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дэвидом Лейбом | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||
| Пентаграммы природы | ||||||||||||||||||||||||||||||||||||||||
Цель: Учащиеся смогут использовать алгебраические понятия при изучении природы. Цель: Учащиеся будут использовать геометрию и концепцию соотношений и применять их для измерения предметов, встречающихся в природе. Материалы: Пятилепестковые цветы, Яблоки, Доллары, Морская звезда. Фокус: Показать фильм: Дональд Дак в стране математики (его можно получить через Library Media Services, 259 долларов США) Процедура:
Оценка: Попросите учащихся сообщить, что они обнаружили с помощью различных материалов. Они нашли золотые треугольники? Что помогло? Что нужно исправить? | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дженнифер Гарретсон | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||
| Деятельность полосы Мебиуса | ||||||||||||||||||||||||||||||||||||||||
Для этого задания вам понадобится пять полосок бумаги на каждого учащегося.
| ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Стивом Бикслером | ||||||||||||||||||||||||||||||||||||||||
Ссылки: Этот проект разработан: pkelley@informns. | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||
| Теорема Пифагора с танграммами | ||||||||||||||||||||||||||||||||||||||||
Цель: Использование танграмм для введения теоремы Пифагора. Цель: Студенты будут использовать танграммы как введение в пифагорейский язык. Теорема. Материалы: набор Tangram (квадрат 4 x 4 дюйма), бумага, карандаш Чтобы у каждого ученика было достаточно деталей для некоторых из этих заданий, вы может позволить студентам работать в парах или предоставить каждому студенту более один набор танграмм. Знакомство с Пифагором Шаг 1 Шаг 2 Шаг 3 Шаг 4 Шаг 5 Шаг 6 (Вот! Ваши ученики только что открыли теорему Пифагора !!!) Это прекрасная возможность поделиться со своими учениками историей Пифагор и как он разработал эту теорему. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||
| Действие формулы Эйлера | ||||||||||||||||||||||||||||||||||||||||
Название урока: Формула Эйлера, зубочистки и мармеладки. Предметная область: Геометрия, предалгебра Уровень оценки: Восьмой Описание или формулировка результата: Обнаружив информацию о плоских сетях и трехмерных объектах, учащиеся смогут продемонстрировать, как удовлетворить формулу Эйлера. Цели:
Для оценки понимания учащимся представленного материала будут даны устные вопросы и ответы, а также тест с карандашом и бумагой из десяти вопросов. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Яном Свенсоном | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||
| Площадь и объем поверхности | ||||||||||||||||||||||||||||||||||||||||
Это упражнение должно научить ученика вычислять объем и площадь поверхности цилиндра.Эту деятельность можно легко связать с историей, обсуждая, как древние могли измерять объем или даже длину до того, как существовала стандартизированная система измерения. Процедура:
| ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Линдси Истридж | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||||||||
| Магические круги Создание усеченного тетраэдра.  | ||||||||||||||||||||||||||||||||||||||||
Я приобрел это занятие во время семинара за 259 долларов США в Уичито, штат Канзас, под названием «Математика в понедельник вечером».Я учил этому классу от третьего класса до колледжа. Это упражнение помогает развивать, укреплять и даже может использоваться для пополнения словарного запаса по математике. Это задание можно выполнить с разными уровнями обучения, просто изменив словарный запас, чтобы он соответствовал уровню навыков, с которым вы работаете. Это отличное упражнение на слушание / мелкую моторику. (Ключевые слова указаны в скобках.) Материалы: один 7-дюймовый бумажный круг, карандаш и линейка Посмотрите на форму, которую вы держите.Опишите это. Это ( круг ). Посмотрите на внешний край вашего круга. Как называется расстояние по внешней стороне круга? ( Окружность ) Сложите круг прямо пополам и хорошо согните его. Раскройте круг, полученная складка — это ( диаметр ) круга. Держите кружок на концах складки. Снова сложите круг пополам, но на этот раз совместите конечные точки складки. Раскройте свой круг, это тоже диаметр? Откуда вы знаете? Линии ( пересекаются с )? Да. Есть ли что-то особенное в том, как эти линии пересекаются? Они образуют четыре угла 90 o (или прямых). Этот особый тип пересечения называется ( перпендикуляр ). Поместите точку, не больше ширины карандаша, в точке соединения складок. Это называется ( центр ) круга. Карандашом обведите одну из линий от центра к краю круга. Эта линия от центра называется (радиус ). Загните один из внешних изогнутых краев круга, пока он не коснется точки в середине. Хорошо согните. Раскройте складку и посмотрите на только что сделанную складку. Это диаметр? Это радиус? Почему или почему нет? Эта линия называется ( аккорд ). Посмотрите на изогнутую часть круга между точками, где эта линия касается внешней стороны круга. Возьмите противоположную сторону вашего круга и сложите его так, чтобы изогнутая часть касалась центра, а нижняя часть образовывала идеальную точку. Ваш круг будет похож на мороженое ( рожок ). Хорошо согните. Сложите верхнюю часть рожка мороженого вниз, пока изогнутая часть не коснется центра круга.Верхние углы должны образовывать идеальные точки, хорошо сгибаться. Теперь опишите свою форму. ( Треугольник ) Вы замечаете что-нибудь особенное в этом треугольнике? Посмотрите на все ( угла ), они такие же, как и все стороны одинаковые. Этот треугольник называется ( равносторонний и / или острый треугольник ). Вы также можете использовать ( равносторонний ). Сложите новый треугольник пополам, совместив две точки.Хорошо мнется. Новое прекращение делит треугольник пополам, эта линия называется ( высота или высота ). Можете ли вы выяснить что-нибудь еще об этом треугольнике? Это ( прямоугольный треугольник ). Раскройте прямоугольный треугольник до равностороннего треугольника. Возьмите верхний угол большого треугольника и сложите его. Сгибая по сгибу по высоте, вы можете совместить верхнюю точку до нижней линии сгиба.Внутри вы увидите три треугольника поменьше. Переверните бумагу, чтобы не было видно складок. Как называется эта форма? Поскольку он имеет четыре стороны, его можно классифицировать как ( четырехугольник ). Поскольку у этого четырехугольника две стороны, которые являются ( параллельными ) и двумя, которые не являются, он также называется ( трапеция ). Переверните его так, чтобы теперь были видны все складки.Сложите один из внешних треугольников так, чтобы он лежал прямо поверх центрального треугольника. Переверните его и опишите форму, которую вы сейчас видите. Это не воздушный змей, в небе летают воздушные змеи. Это не бриллиант, я ношу бриллианты на пальцах. В математике эта форма называется ( ромб ). Снова переверните фигуру и снова сложите последний внешний треугольник на центральный. У вас должен получиться равносторонний треугольник меньшего размера. Раскройте все три маленьких треугольника.Соедините три свободные точки вместе, чтобы у вас получилась пирамида ( ). На этом этапе вы можете обсудить ( грани ) ( ребра ) ( точки ) ( вершины ) ( основание ) и тот факт, что это ( треугольная пирамида ), а не квадратная пирамида, как в Египте. Откройте пирамиду до большого равностороннего треугольника. Согните одну из точек так, чтобы она касалась точки посередине. Какую форму вы воссоздали? Трапеция хоть и не традиционной формы, ее все же можно идентифицировать как трапецию. Сложите еще одну точку так, чтобы она касалась точки посередине. Какая у вас форма? ( Пентагон ) Несмотря на то, что это не та традиционная форма, к которой вы привыкли, у нее все еще есть пять сторон, поэтому он по-прежнему классифицируется как пятиугольник. Теперь сложите последнюю точку. Какой он сейчас формы? ( Hexagon ) Обсудите ( плоскость ) фигурки. Переверните на другую сторону и вставьте один из углов в лоскут на противоположной стороне треугольника. Возможно, вам придется попробовать более одного. Выберите тот, который вам больше всего подходит. Сдвиньте последний угол под / внутрь других. Вы создали ( усеченный тетраэдр )! Для любой формы во время этого упражнения вы можете попросить учащихся вычислить площадь поверхности, объем, периметр и / или площадь. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||
| Эксперимент с водяным шлангом. | ||||||||||||||||||||||||||||||||||||||||
Это задание можно выполнить за один урок. Чтобы ответить на вопросы и сделать выводы, может потребоваться еще один урок, в зависимости от продолжительности вашего урока. Прекрасно подходит для весны, когда у школьников и учителей весенняя лихорадка.Его цель — найти оптимальный угол для достижения наибольшего расстояния. В зависимости от того, какой класс вы преподаете, это задание можно изменить. История: Простой транспортир — старинный прибор. Создан первый комплексный транспортир для определения положения лодки на навигационных картах. Названный трехрычажным транспортиром или указателем станции, он был изобретен в 1801 году Джозефом Худдартом, капитаном ВМС США. Центральный рычаг неподвижен, а два внешних поворотных, их можно установить под любым углом относительно центрального рычага. Материалы:
Присоедините садовый шланг к водопроводному крану и отрегулируйте поток воды так, чтобы он находился под постоянным давлением. Начните с угла 0 градусов к земле, измерьте и запишите расстояние, которое поток проходит в горизонтальном направлении по земле.Повторите эти действия для углов 20 o , 30 o , 45 o , 70 o и 75 o . Вопросы и выводы:
URL: http://inventors.about.com/science/inventors/libr…/blmeasurement.htm?terms=protractor+histor 14.06.00 20:30 | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Эми Траутман | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||
| Расчет числа Пи. | ||||||||||||||||||||||||||||||||||||||||
Примерно 4000 лет назад люди впервые начали понимать пи. Считалось, что его стоимость была около трех. Сегодня мы используем лучшее приближение числа пи. Это 3,14. Пи — иррациональное число. Это означает, что он не повторяется в шаблоне. Пи определяется как отношение длины окружности к диаметру той же окружности. А теперь небольшое упражнение, которое поможет вам определить число Пи. Материалы:
Сначала на листе бумаги сделайте 4 столбца с надписью: объект, диаметр, окружность и соотношение.(См. Пример ниже.) Оберните веревку вокруг объекта. Это измеряет окружность объекта. Измерьте строку с помощью измерительной линейки. Запишите значение в столбец с надписью «длина окружности». Затем измерьте расстояние прямо поперек объекта. Поместите это значение в столбец, обозначенный как диаметр. Теперь возьмите длину окружности, разделенную на диаметр. Поместите это в столбец с надписью «Соотношение». Это близко к пи? Убедитесь, что вы приняли соотношение до трех или четырех десятичных знаков.
| ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джереми Траутманом | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||
| Активность тесселяции. | ||||||||||||||||||||||||||||||||||||||||
Класс: 5 или 6 Время: 20-30 минут уроки Необходимые материалы: Смесь многоугольников, таких как геоблоки, бумага, карандаш и цветные карандаши. Урок 1 Фокус: Поместите различные формы наверх. Обсудите в классе сходство и различие форм.Сообщите учащимся, что фигуры представляют собой многоугольники (фигура на близком расстоянии). Расскажите о концепции мозаики и о том, как не должно быть разрывов или перекрытий. Продемонстрируйте концепцию наверху, используя квадрат. Задание: Попросите учащихся предсказать, какие фигуры будут мозаичными, а какие нет. Составьте диаграмму, показывающую результаты прогнозов студентов. Дайте каждому столу (или ученику, если возможно) набор фигур. Попросите учащихся самостоятельно определить, будет ли фигура мозаикой. Заключение: Обсудите всем классом, какая форма плитки на самом деле, а какая нет. Сравните открытия с предсказаниями на картах. Завершение: Предложите учащимся определить многоугольник и то, что они узнали о нем, в короткой дневной записи. Урок 2 В фокусе: Просмотрите концепции многоугольника и мозаики. Расскажите о термине тесселяция и о том, как он соотносится с уроком 1.Обсудите концепции скольжения, вращения (поворота) и отражения (переворачивания) и продемонстрируйте их на потолке. Задание: Попросите учащихся выбрать две или более фигур. Попросите учащихся раскрасить каждую форму в один цвет. Попросите учащихся обвести фигуры черным маркером, если это слайд. Обведите фигуру синим маркером, если это поворот. Отражение следует обвести красным маркером. Заключение: Попросите учащихся поднять руки, когда они закончили.Инструктор проверит результаты. Замыкание: Обсудите, какие различные формы объединяют в мозаику результаты построения диаграмм. Разрешите учащимся записывать свои выводы. Урок 3 Фокус: Просмотрите предыдущие уроки. Обсудите, как студенты будут применять свои знания техники тесселяции для поиска концепции в искусстве. Активность: Предоставьте несколько работ различных художников, в том числе несколько работ М.К. Эшер. Предложите учащимся изучить различные произведения искусства, чтобы выяснить, использует ли художник технику мозаики. Заключение: Попросите учащихся обсудить, что они нашли в деталях. Выскажите гипотезу, почему художники использовали или не использовали технику тесселяции. Окончание: Попросите учащихся записать свои выводы в своих дневниках. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено CiCi Naifeh | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||||||||
| Площадь и объем геометрических фигур. | ||||||||||||||||||||||||||||||||||||||||
Площадь геометрических фигур Цель: Дать студенту возможность попрактиковаться в вычислении площади различных геометрических фигур. Необходимые материалы: Использованные журналы, ножницы, линейки, клей, плотная бумага и калькуляторы Процедура:
Чтобы подчеркнуть процесс решения проблемы (решить проблему с помощью метода, о котором вы уже знаете), дайте учащимся упрощенную картинку, взятую из книжек-раскрасок, и попросите их оценить площадь изображения. Используя описанный выше метод, учащиеся должны разделить изображение по формам и вычислить площадь каждой формы, а затем просуммировать формы областей, чтобы оценить площадь изображения. Практическое применение: Если кто-то собирается красить комнату, необходимо определить общую площадь всех стен, чтобы купить нужное количество краски. Объем геометрических фигур Цель: Дать студентам возможность визуально понимать трехмерные геометрические формы и практиковаться в вычислении объема Необходимые материалы: Самодельные ингредиенты для игр, плита, кастрюля, ложка, линейки и калькуляторы. Процедура:
| ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||||||||
| Какой формы ваша земля? | ||||||||||||||||||||||||||||||||||||||||
Цели:
Материалы: Для каждого учащегося или группы: один лист миллиметровой бумаги, приклеенный или приклеенный на гофрированный картон или жесткий пенопласт; замкнутая петля из бечевки, длиной 20 сантиметров; приблизительно шесть прямых кнопок или канцелярских кнопок на учащегося или группу; карандаш и бумага для записей. Историческая справка: Согласно римской мифологии Дидона была дочерью царя Тира. Ее брат Пигмалион убил ее мужа, и она сбежала, опасаясь за свою безопасность. Дидона пересекла Средиземное море со всем своим богатством и некоторыми товарищами и высадилась в североафриканском королевстве Ливия. Здесь она искала землю в качестве убежища для своей группы. Король согласился дать ей столько земли, сколько она сможет покрыть шкурой быка. Дидона кое-что знала о геометрии и хотела как можно больше земли.Она разрезала шкуру быка на тонкие полоски, а затем соединила их в одну длинную прядь. Как вы думаете, какую форму она заключила? Организация: Учащиеся могут выполнять это задание индивидуально или в группах. Возможные групповые роли для четырех участников: двое учеников должны создавать формы, один — для вычисления площадей, а третий — для записи форм, размеров и площадей. Каждой группе понадобится один набор материалов, как описано выше: миллиметровая бумага на доске, кнопки и веревка. Задание: Учащиеся должны использовать веревку и канцелярские кнопки, чтобы разложить плоские фигуры на сетке.Студентам необходимо будет вычислить площадь каждой фигуры, которую они создают, поэтому выбранные формы будут зависеть от базовых знаний студентов. Предлагаемые фигуры: квадрат, прямоугольники, треугольники и круг. Напомните учащимся, что они могут образовывать более одного прямоугольника и более одного треугольника. Студенты должны рассчитать площади для каждой сформированной фигуры и решить, какую форму, по их мнению, следует выбрать Дидоне. Примечание: , если это используется как упражнение для представления областей плоских фигур, учащиеся могут находить области, считая квадраты.В качестве дополнительного задания учащиеся должны использовать формулы площади. Следующая таблица или аналогичная может быть предоставлена для ведения учета:
Вопросы для обсуждения:
В конце концов Дидона отмерила форму полукруга, соединив одну точку на берегу с другой. Таким образом, вода составляла одно из ее требований, и у нее было дополнительное преимущество — выход к морю. Ей нужно было только использовать шкуру, чтобы оградить землю, поэтому выделенная ею территория была как можно больше и желательна. Король Ливии сдержал свое слово и отдал ей землю.Зарекомендовала себя умная Дидона, будущая королева Карфагена. Попросите учащихся развязать петли из веревок и с помощью 20-сантиметровых прядей образовать полукруги по краям решетки. Вычислите площадь полученного таким образом полукруга, чтобы понять, насколько умен Дидона. Связанные действия: Следующий трюк может стать забавным введением в занятие. Принесите в класс лист бумаги размером, может быть, с лист бумаги для принтера.Спросите своих учеников: как вы думаете, я могу вырезать отверстие в этом листе бумаги и протолкнуть его (впишите имя какого-нибудь ученика в классе)? Когда студенты выражают свой скептицизм, прорежьте в бумаге большое отверстие, просуньте руку в отверстие и осторожно толкните выбранного ученика. Затем достаньте свежий лист бумаги с очень маленьким отверстием. Спросите, как вы думаете, я смогу провести (того же ученика) через лист бумаги с этим отверстием? Общая реакция будет такой, что вы, вероятно, не сможете, хотя некоторые студенты будут искать другой трюк. Чтобы показать им, что вы можете делать то, что вы сказали, возьмите лист бумаги с таким же маленьким отверстием и прорезями, как показано на схеме ниже. Вы можете использовать уже имеющийся у вас лист и вырезать прорези, пока они ждут, но это займет много времени. Откройте прорези, чтобы сформировать одну огромную бумажную петлю, и наденьте ее прямо на голову учеников. Вы сделали это! | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Лори Кисс | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||||||||
| Геометрический текстильный дизайн. | ||||||||||||||||||||||||||||||||||||||||
Иногда учащимся сложно соотнести математику с реальным миром; Следовательно, эта деятельность в области геометрического текстильного дизайна будет акцентировать внимание на геометрических формах и узорах в сочетании с художественным дизайном, компьютерными приложениями и карьерными возможностями. Цель: Для каждого ученика разработать свой собственный геометрический квадрат из текстиля, из которого будет изготовлено лоскутное одеяло. Необходимые материалы: Тканевые квадраты геометрической формы (5 дюймов х 5 дюймов), шаблонная бумага, цветные карандаши, белые тканевые квадраты (5 дюймов х 5 дюймов), обрезки картона, малярная лента и краска для ткани Процедура:
| ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||||||||
| Изготовление многогранников. | ||||||||||||||||||||||||||||||||||||||||
Многогранник — это геометрическая фигура, которая является трехмерной версией плоского многоугольника (двумерного). Всего пять правильных многогранников. Это тетраэдр (4 грани), шестигранник или куб (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).Ниже представлены выкройки двух многогранников, которые можно воспроизвести и трансформировать в трехмерные фигуры. Щелкните на фигурах, чтобы открыть окно с фигурой внутри для облегчения печати. | ||||||||||||||||||||||||||||||||||||||||
| Предоставлено Сьюзен Истман | ||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||||||||
Геометрический рисунок по выгодной цене — Отличные предложения по геометрическому рисунку от глобальных продавцов геометрических рисунков
Отличные новости !!! Вы попали в нужное место для геометрического рисунка.К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress. У нас буквально тысячи отличных продуктов во всех товарных категориях. Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.
Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.
AliExpress никогда не уступит по выбору, качеству и цене. Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны. Но вам, возможно, придется действовать быстро, поскольку этот геометрический рисунок в кратчайшие сроки станет одним из самых востребованных бестселлеров. Подумайте, как вам будут завидовать друзья, когда вы скажете им, что купили свой геометрический рисунок на AliExpress.Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете еще больше сэкономить.
Если вы все еще не уверены в геометрическом рисунке и думаете о выборе аналогичного товара, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам решить, стоит ли доплачивать за высококлассную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь.А если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. и ожидаемая экономия.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца.Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз. Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.
А если вы новичок на AliExpress, мы откроем вам секрет.Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress. Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, вы сможете приобрести геометрический рисунок по самой выгодной цене.
У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы.На AliExpress отличное качество, цена и сервис всегда в стандартной комплектации. Начните самый лучший шоппинг прямо здесь.
Область геометрических форм — введение, типы, формулы, примеры и часто задаваемые вопросы
×
Извините !, эта страница сейчас недоступна для добавления в закладки.
Область фигур
Область фигур — это пространство, окруженное или ограниченное границей периметра данных геометрических фигур.Это измерение, которое определяет величину двумерной формы или плоской пластинки на плоскости. Форма пластинки включает в себя двухмерные фигуры, которые можно легко нарисовать на плоскости, например квадрат, прямоугольник, треугольник, параллелограмм, трапецию и т. Д. Области фигур, такие как квадрат, прямоугольник, треугольник, параллелограмм, трапеция, круг — это диапазон покрыты ими в космосе. В этой статье вы изучите области геометрических фигур, формулы площади для различных фигур, площадь двухмерных фигур, площадь трехмерных фигур и т. Д.
Многоугольники
Многоугольник — это двухмерная форма, состоящая из прямых линий. Некоторыми примерами многоугольников являются треугольник, пятиугольник, шестиугольник, квадрат, прямоугольник и т. Д. Само название этих форм определяет общее количество сторон, включенных в форму. Например, треугольник имеет 3 стороны, а прямоугольник — 4 стороны. Следовательно, любая форма, состоящая из соединения трех линий, называется треугольником, тогда как формы, состоящие из соединения четырех линий, известны как четырехугольники.Область — это диапазон внутри границы / периметра, который необходимо исследовать.
Площадь двумерных фигур
В геометрии двумерные формы определяются как плоская фигура или форма, которая включает в себя две меры, такие как длина и ширина. В двумерных формах нет толщины. Площадь и периметр — это две разные меры, используемые для измерения плоских форм. Двумерный рисунок легко нарисовать на обычной бумаге. Некоторые из примеров двумерных фигур — прямоугольник, треугольник, квадрат, трапеция и т. Д.
Площадь 2-х фигур Формула —
Обычно площадь фигур определяется как количество цвета краски, необходимое для покрытия любой поверхности одним слоем. Вот методы расчета площади на основе сторон, включенных в форму, как описано ниже:
[Изображение будет загружено в ближайшее время]
Здесь вы можете увидеть формулы площади для различных фигур в табличном формате.
Формы | Площадь | Условные обозначения |
Окружность | π5 9000 9000 9000 9000 π5 9000 900 9000 9000 радиус обозначает радиус | |
Треугольник | ½ × b × h | B обозначает ширину, а h обозначает высоту |
Прямоугольник | L × w | L10 обозначает длину |
Параллелограмм | b × h | B означает ширину, а h означает высоту |
Трапецию | ½ 900 (a + 0) x h + b) — длина параллельных сторон, а h — высота трапеции | 900 06|
Эллипс | Π ab | Здесь A = малая ось ½ b = малая ось 1/2 |
Рисование геометрической перспективы — манекены
27
Геометрическая перспектива (иногда называемая линейной перспективой ) заставляет объекты на рисунке выглядеть так, как будто они уходят в далекое пространство, становясь тем меньше, чем дальше они от вас. .
Геометрическая перспектива также может создать иллюзию того, что вы находитесь над или под объектом рисунка. Использование геометрической перспективы делает ваши рисунки трехмерными (а не плоскими) и более реалистичными.
Чтобы начать работу с геометрической перспективой, вам сначала необходимо ознакомиться со следующим:
- Линия горизонта: Воображаемая горизонтальная линия, иногда называемая уровнем глаз , , которая разделяет линию вашего зрения, когда вы смотрите прямо перед собой.
- Объекты ниже этой линии находятся ниже уровня ваших глаз, а объекты выше этой линии — выше уровня ваших глаз. Художники рисуют линии горизонта, чтобы точно определить перспективу на своих рисунках.
- Линии перспективы: Прямые линии, проведенные под углом от краев объектов, возвращаются в воспринимаемое далекое пространство, пока они, наконец, не сходятся в точке на линии горизонта. Эти линии устанавливают ориентиры для рисования объектов в правильной перспективе.
- Угловые линии: Прямые линии, которые не параллельны и не перпендикулярны линии горизонта.
- Точка исчезновения: Точка на линии горизонта, где угловые линии перспективы объекта визуально продолжаются за его края и в конечном итоге сходятся.
- Объекты становятся все меньше и меньше по мере приближения к точке схода, и в этот момент кажется, что они полностью исчезают (или исчезают). Некоторые объекты могут иметь даже более одной точки схода.
Линии объектов, которые параллельны или перпендикулярны (под прямым углом) к линии горизонта, не кажутся возвращающимися в космос (например, верхний, нижний и боковые края здания при виде спереди) и, следовательно, не встречайте точку схода.
Создание линии горизонта чертежа
Всегда проводите линию горизонта параллельно верху и низу квадратной или прямоугольной области рисования. Вы определяете уровень глаз зрителя, выбирая положение линии горизонта. Вы контролируете, будете ли вы
Плоские и твердые Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, Открытый и закрытый Лист 1, Лист 2, 2D и 3D описания Лист 1 , Лист 2, Лист 3, Лист 4, Лист 5, Правильные / неправильные многоугольники Лист 1, Лист 2, Лист 3, Стороны, края, грани и вершины Лист 1, Лист 2 , Лист 3, Лист 4, Лист 5, | |
3D Nets Лист 1, Лист 2, Лист 3, Лист 4, Круг Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, Перспективы Лист 1 , Лист 2, Лист 3, Лист 4, | |
График Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, | |
Вращательная симметрия Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, Линии симметрии Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, | |
Типы Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, Область Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, Найти неизвестный угол Лист 1, Лист 2, | |
Радиус, диаметр, окружность Лист 1, Лист 2, | |
Квадраты и прямоугольники Лист 1, Лист 2, Лист 3, Параллелограмм и трапеция Лист 1, Лист 2, Лист 3, Составные и неправильные фигуры Лист 1, Лист 2 , Лист 3, Лист 4, Проблемы Word Лист 1, Лист 2, | |
Определить острые, правые, тупые и прямые углы Лист 1, лист 2, лист 3, лист 4, лист 5, Измерение Лист 1, лист 2, лист 3, лист 4, лист 5 , | |
Аналогичные и совпадающие Лист 1, | |
Объем Лист 1, Лист 2, Лист 3, Площадь поверхности Лист 1, Лист 2, Лист 3, | |
Параллельные, перпендикулярные и пересекающиеся Лист 1, лист 2, лист 3, Линии, сегменты линий, лучи Лист 1, лист 2, лист 3, | |
Координаты: десятичные и отрицательные числа Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, Карты Лист 1 Квадранты I, II, III, IV Лист 1 , Лист 2, Лист 3, Лист 4, Лист 5, Квадранты (X, Y) Лист 1, Лист 2, Лист 3, Лист 4, Лист 5, |

 Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
 Когда с фигурами станет все предельно ясно — дайте ребенку бланк №2 с недостающими деталями и скажите ему, что на этом листе геометрические фигуры немного испортились. И теперь его задача — исправить их для получения точно такого результата, как на бланке №1.
Когда с фигурами станет все предельно ясно — дайте ребенку бланк №2 с недостающими деталями и скажите ему, что на этом листе геометрические фигуры немного испортились. И теперь его задача — исправить их для получения точно такого результата, как на бланке №1. Упражнение «Найди геометрические фигуры»
Упражнение «Найди геометрические фигуры»
 Гленко / Макгроу Хилл. Огайо. 1998 г.
Гленко / Макгроу Хилл. Огайо. 1998 г. дано.
дано.
 Каждый
полоса должна быть примерно 3 х 14 дюймов. Каждому ученику также понадобится
около двух футов ленты, подойдет либо прозрачная лента, либо клейкая лента),
ножницы и ручка или карандаш.
Каждый
полоса должна быть примерно 3 х 14 дюймов. Каждому ученику также понадобится
около двух футов ленты, подойдет либо прозрачная лента, либо клейкая лента),
ножницы и ручка или карандаш. Если отрезать 1/3 пути, что будет
случиться? Сделай это. Примечание: к этому времени многие студенты откажутся от
угадывает часть деятельности или дает абсурдные мнения.
Если отрезать 1/3 пути, что будет
случиться? Сделай это. Примечание: к этому времени многие студенты откажутся от
угадывает часть деятельности или дает абсурдные мнения. k12.mn.us
k12.mn.us ( c > a ; c > b ; a + b > c )
( c > a ; c > b ; a + b > c ) ) и для стороны «C». (Все семь частей танграма.)
) и для стороны «C». (Все семь частей танграма.)
 Какие структуры вы можете придумать, которые почти кричат вам Геометрия? Бейсбольные бриллианты? Баскетбольная площадка? Мост «Золотые ворота? Как насчет центра EPCOT во Флориде?
Какие структуры вы можете придумать, которые почти кричат вам Геометрия? Бейсбольные бриллианты? Баскетбольная площадка? Мост «Золотые ворота? Как насчет центра EPCOT во Флориде?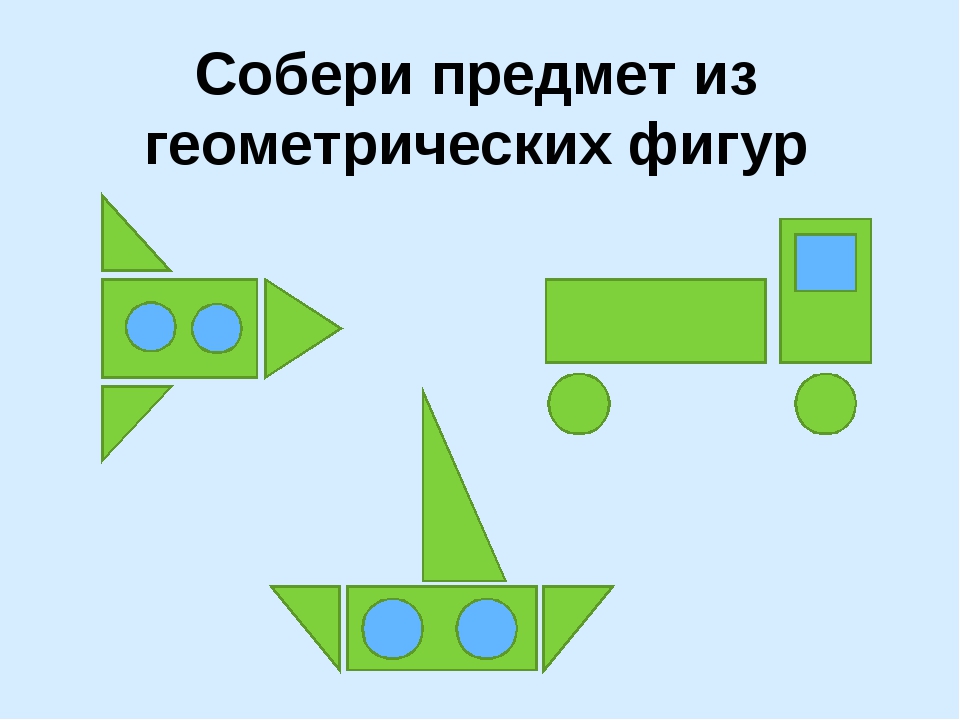 На этом этапе мы введем формулу Эйлера ( V — E + F = 2 ) и продемонстрируем, как удовлетворить ее с помощью нашей модели.
На этом этапе мы введем формулу Эйлера ( V — E + F = 2 ) и продемонстрируем, как удовлетворить ее с помощью нашей модели. Сверните лист бумаги в высокий цилиндр, затем скотчем. Скатайте другой лист бумаги того же размера в более короткий и широкий цилиндр. Спросите учащихся, что, по их мнению, вмещает больше (объем больше).
Сверните лист бумаги в высокий цилиндр, затем скотчем. Скатайте другой лист бумаги того же размера в более короткий и широкий цилиндр. Спросите учащихся, что, по их мнению, вмещает больше (объем больше).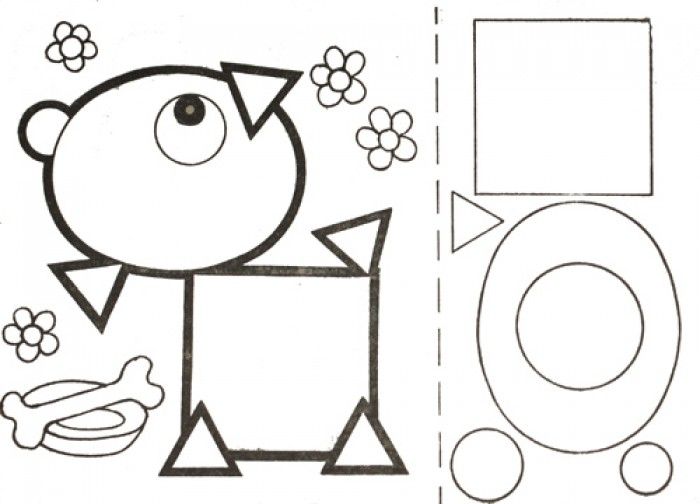
 Это называется ( arc ). Можете ли вы найти другие дуги на своем круге?
Это называется ( arc ). Можете ли вы найти другие дуги на своем круге?