Как из круга сделать шестиугольник

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К.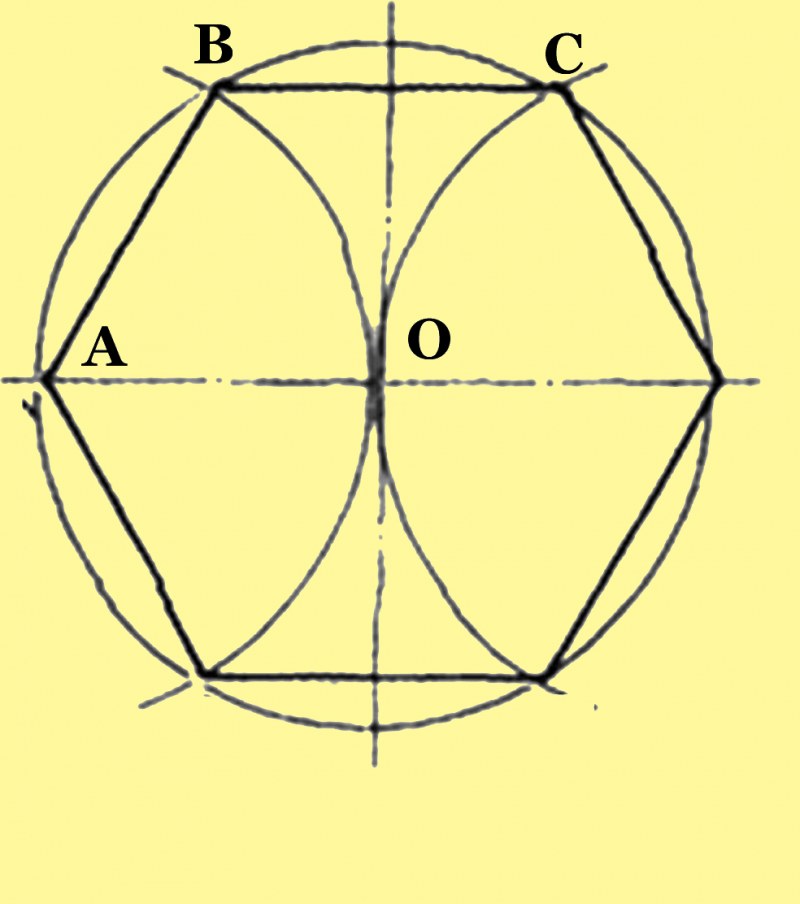 Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.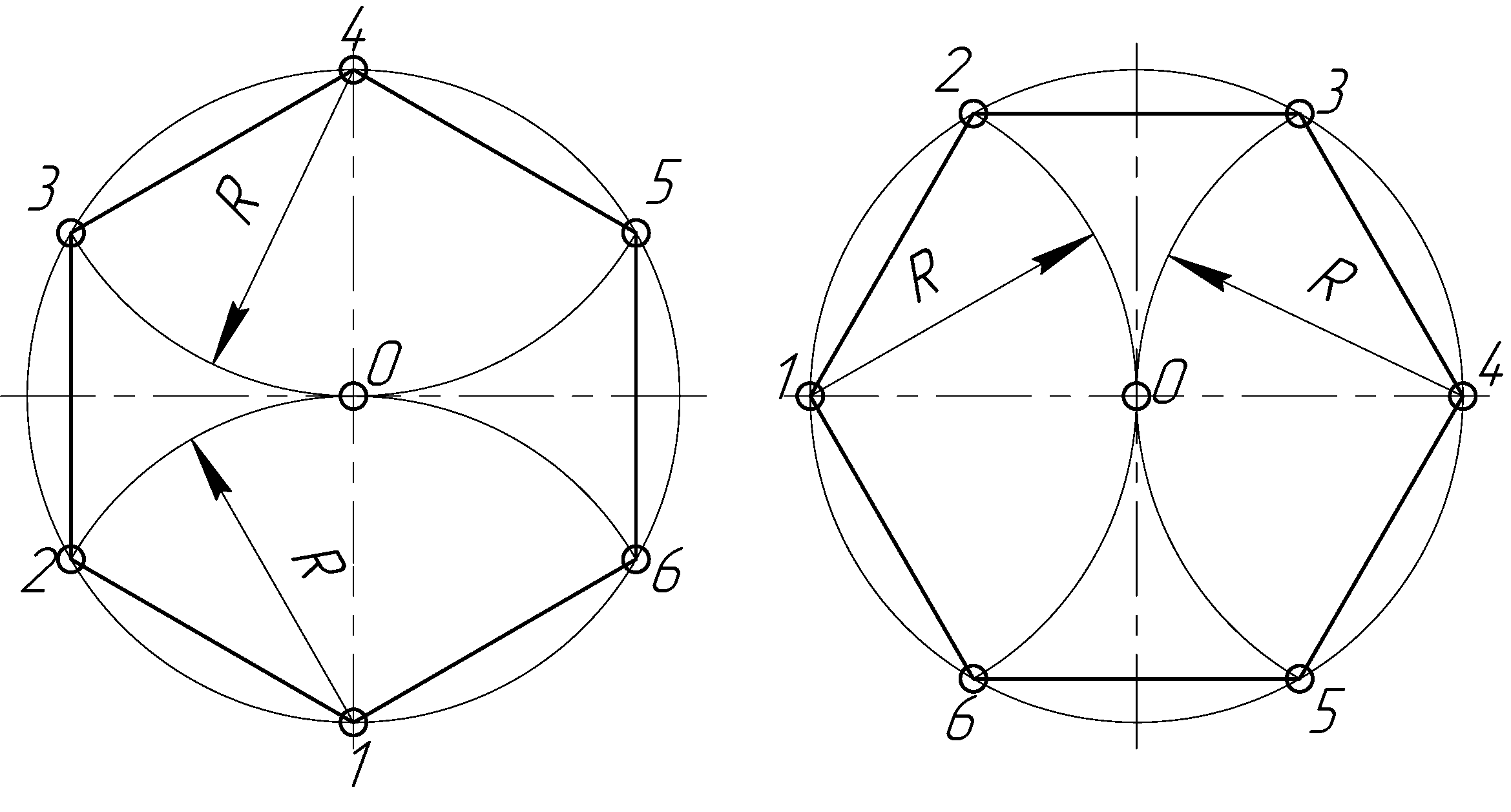

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…

Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…

Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…

Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…

Здравствуйте коллеги. В этом уроке узнаем, как нарисовать шестиугольник в перспективе.

Как вписать его фронтально в окружность мы смотрели в прошлом уроке. Заметьте ничего сложного нет. Нам удалось малыми средствами начертить равнобедренный предмет с шестью вершинами.

Его можно сделать еще проще. Например, отложить шесть радиусов на тело овала. Эта фигура не такая сложная, как с пятью или с семью углами, уроки которых мы рассмотрим в других статьях.

Я не фанат точной науки геометрии. Приходилось рисовать, но без циркуля и угольника не всегда получалось правильно создать картину.

Наша задача показать полную иллюзию пространства на двухмерной плоскости. Нарисуем многоугольник онлайн в перспективе, а для этого нужно знать правила построения.

К примеру, чтобы создать многоугольный узор на потолке, как на картине художника Премацци, нужно знать законы построения.

«Виды залов нового Эрмитажа. Галерея фламандской живописи. »

На картине Гау мы видим интерьер дворца. И все узоры выполнены в рамках законов линейной перспективы.

«Зимний дворец. Петровский зал.»

Посмотрите узор на полу в произведении Жерома Жан-Леона.

«Painting Breathes Life into Sculpture»

Задумывая сюжет в интерьере, нам придется изучать принципы построения.
Как положить шестигранник на плоскость посмотрите видео урок ниже.

Рисуем онлайн многоугольник в перспективе

Делал я его с помощью программы Photoshop, все то же самое можно сделать и на бумаге.
Для рисования нам понадобятся:

Такой небольшой набор инструментов необходим для черчения в живую.

Сам рисунок вы можете посмотреть на видео.

Сделаем акцент, когда шестиугольник вписанный в окружность.

Ниже на фото фигура построена. И, казалось бы, добавить нечего.

Но правильный рисунок будет если его вписать в овал. У нас есть две точки по сторонам квадрата, и появились новые четыре точки. Картинка ниже.

В таком формате он не будет деформированный, вытянутый или сплюснутый. На рисунке будет смотреться правдоподобнее.

По такому же принципу можно сделать фигуру не только горизонтально, но и вертикально.

В таком случае мы сможем выстроить призму. Для этого мы сделаем переднее и заднее основания и соединим их линиями. Эта процедура детально описана в моем платном курсе, можете перейти по этой ссылке.

Вот такой урок получился.
Творческих вам успехов.

Научимся изображать шестигранную призму в различных положениях.

Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.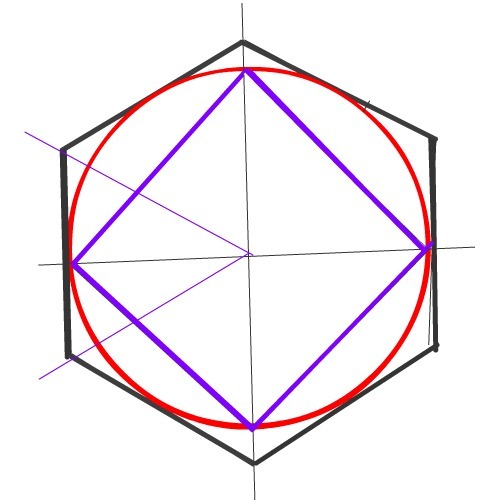 53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.

На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.

Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы

Горизонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.

На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.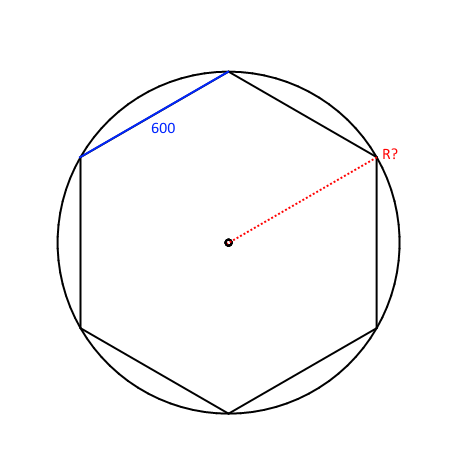

Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).

Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.

Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы

Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс).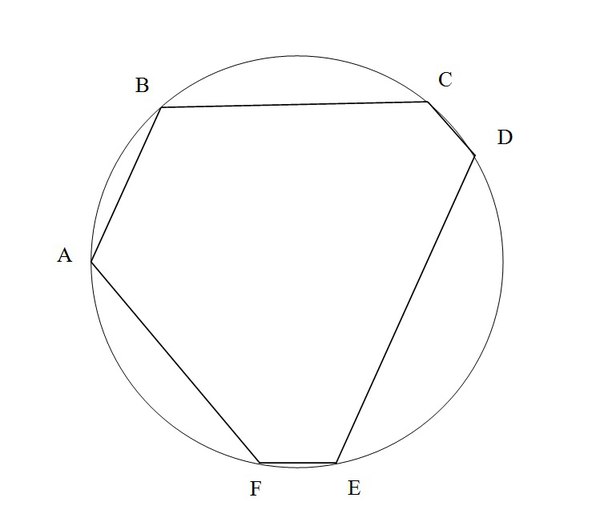 Все вершины шестиугольника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).

Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы

Построение на плоскости | Журнал Ярмарки Мастеров

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?inside=1&wf=&cp=1&vr=1

Нам понадобятся: карандаш, линейка, циркуль.

Построение угла в 60

1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

1. Построим угол 60, кака описано выше.

2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

Построение угла в 90

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

Разделение отрезка на равные части.

1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

Построение правильного пятиугольника.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC. Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G.

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG.

Построение правильного шестиугольника.

1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

Построение правильного семиугольника.

1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G.

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF.

Общий метод построения многоугольников.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G. Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.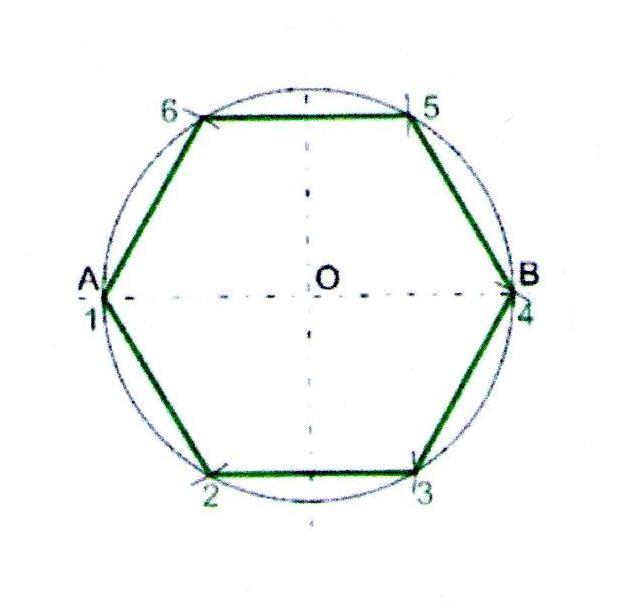

Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника

 

 

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90^º и/или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 2.24). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник.

 

а) б)

Рисунок 2.24

При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 2.25). Соединив полученные точки, получают двенадцатиугольник.

 

а) б)

Рисунок 2.25

 

 

2.2.5 Деление окружности на пять и десять равных частей
и построение правильного вписанного пятиугольника и десятиугольника

 

 

Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 2.26.

 

а) б) в) г)

 

Рисунок 2.26

Половину любого диаметра (радиус) делят пополам (рис. 2.26 а), получают точку А.Из точки А,как из центра, проводят дугу радиусом, равным расстоянию от точки Адо точки 1 до пересечения со второй половиной этого диаметра, в точке В(рис. 2.26 б). Отрезок 1Вравен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности. Делая засечки на окружности (рис. 2.26, в

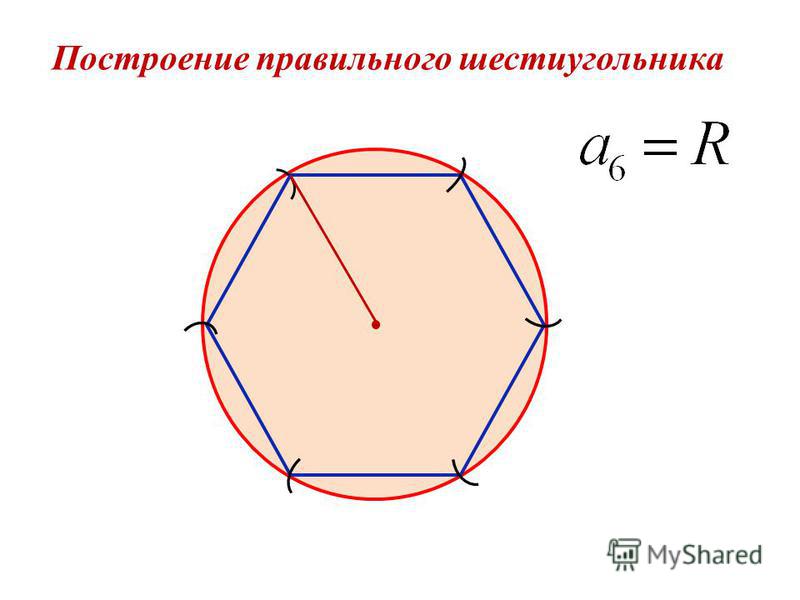) радиусом К,равным отрезку 1В,делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5 (рис. 2.26, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем. Если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 2.26, г).

Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 2.26), но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 2.27, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник(рис. 2.27, б).

 

а) б)

Рисунок 2. 27

2.2.6 Деление окружности на семь и четырнадцать равных
частей и построение правильного вписанного семиугольника и

четырнадцатиугольника

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 2.28 и 2.29.

Из любой точки окружности, например точки А, радиусом заданной окружности проводят дугу (рис. 2.28, а) до пересечения с окружностью в точках В и D. Соединим точки Ви Dпрямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС,делают засечки на окружности в последовательности, показанной на рис. 2.28, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 2.28, в).

Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис.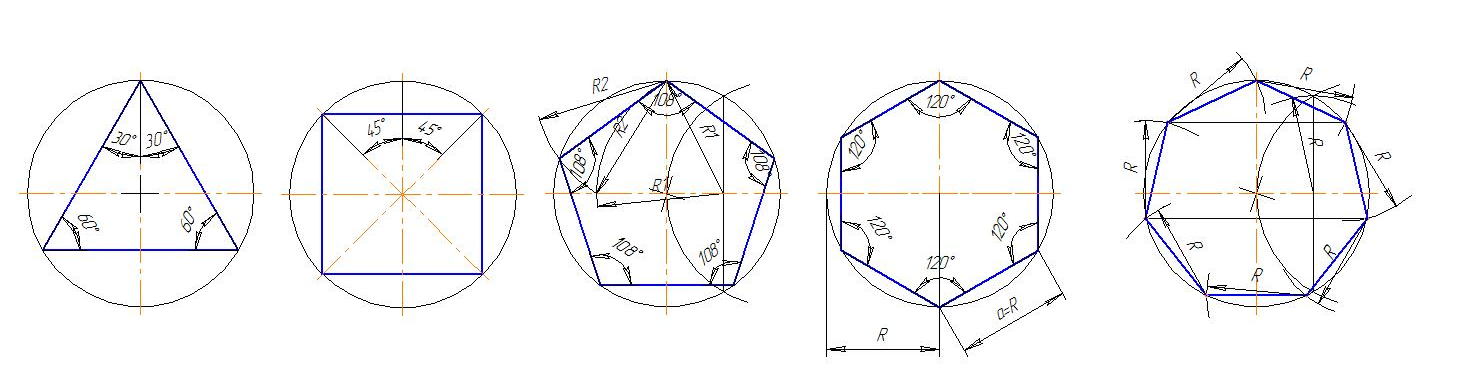 2.29, а).

 

а) б) в)

Рисунок 2.28

Сначала окружность делится на семь равных частей от точки 1, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырнадцатиугольник (рис. 2.29, б).

 

а) б)

Рисунок 2.29

 

 

Построение эллипса

 

 

Изображение окружности в прямоугольной изометрической проекции во всех трех плоскостях проекций представляет собой одинаковые по форме эллипсы.

Направление малой оси эллипса совпадает с направлением аксонометрической оси, перпендикулярной той плоскости проекций, в которой лежит изображаемая окружность.

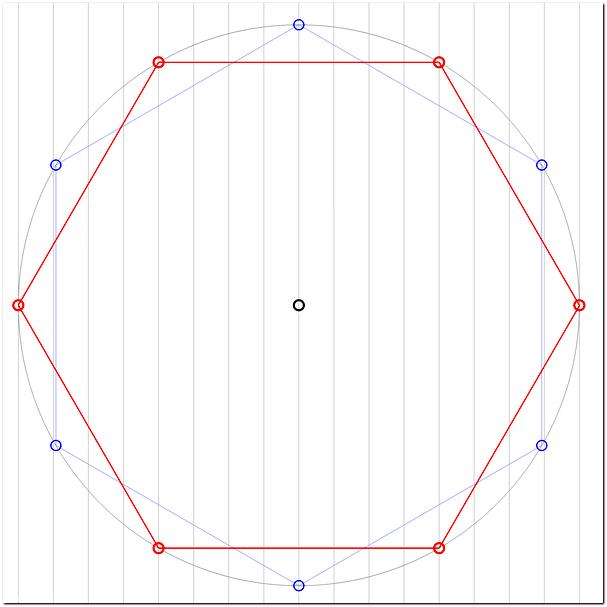
При построении эллипса, изображающего окружность небольшого диаметра, достаточно построить восемь точек, принадлежащих эллипсу (рис.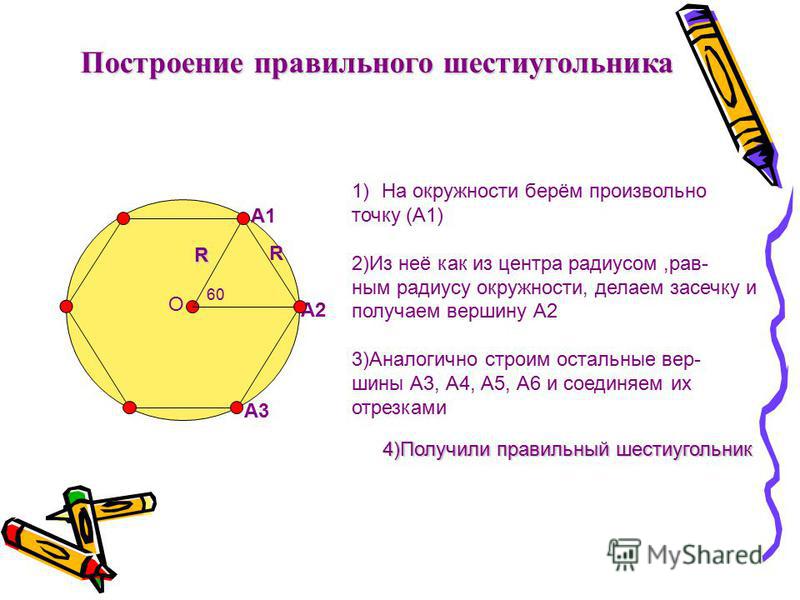 2.30). Четыре из них являются концами осей эллипса (A, B, С, D),а четыре других (N₁, N_2, N_3, N₄) расположены на прямых, параллельных аксонометрическим осям, на расстоянии, равном радиусу изображаемой окружности от центра эллипса.

 

а	б

Рисунок 2.30

Читайте также:

 

Как нарисовать шестигранник без циркуля

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Способ вычерчивания шестиугольника циркулем, линейкой

Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.

Метод выглядит следующим образом:

Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

• циркулем вычерчивается окружность — радиус является размером стороны;
• по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
• находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
• находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.

Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.

Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений.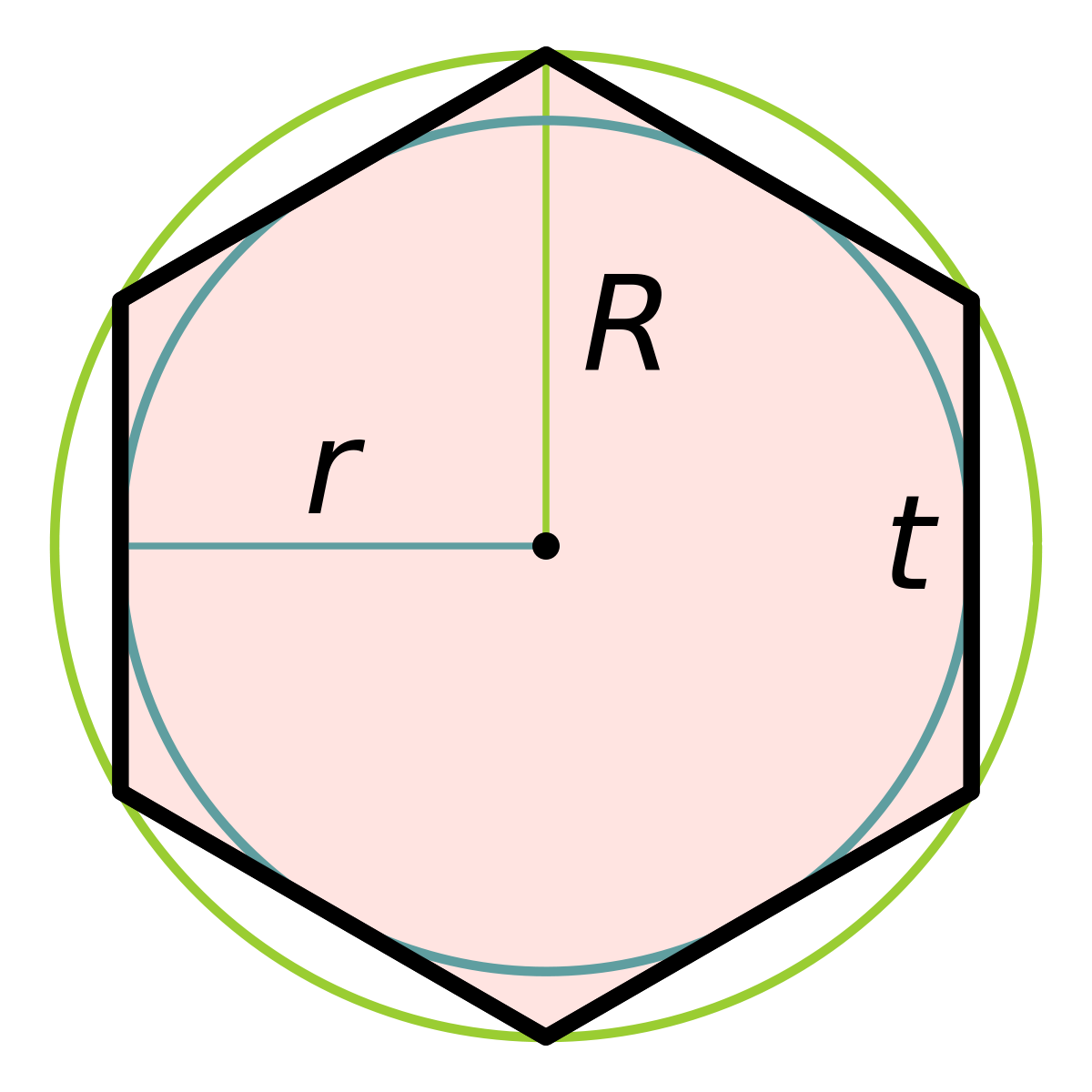 Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

• к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
• на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
• операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
• разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
• уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
• строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
• контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе.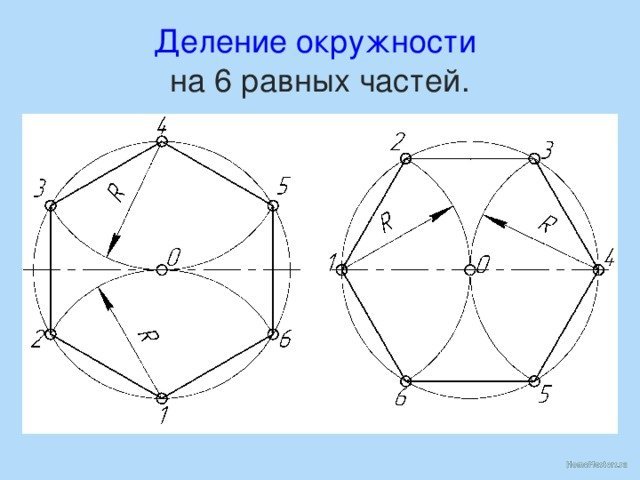 Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

• после вычерчивания центрального отрезка по нему выравнивается рейсшина;
• инструмент откатывается вниз на произвольную величину;
• короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
• скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.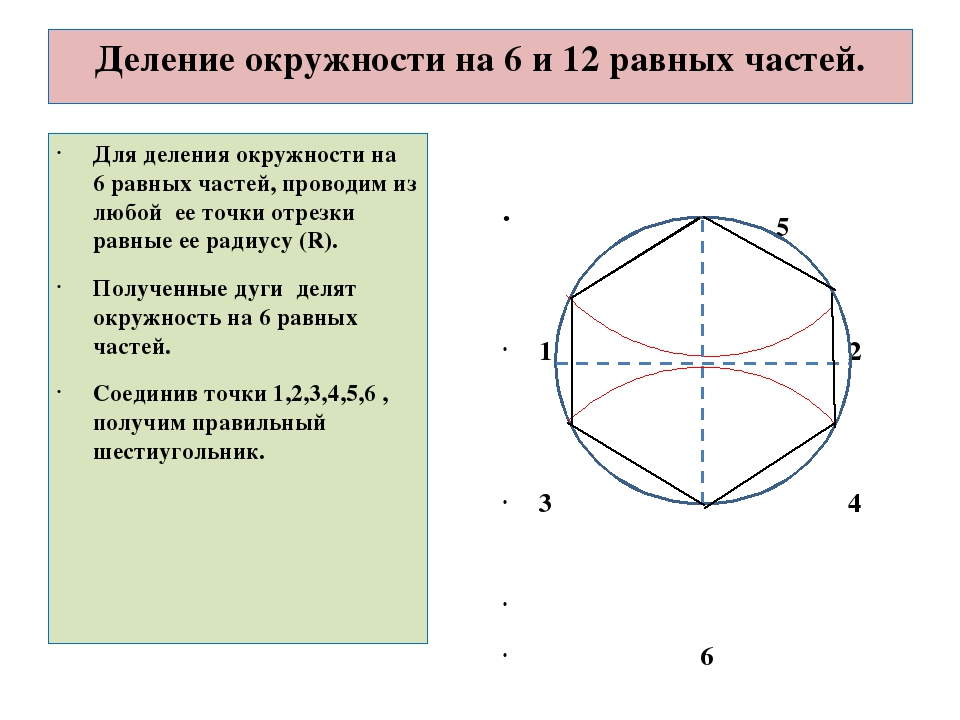

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Popular

Основы черчения

Строительное

Машиностроительное

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг.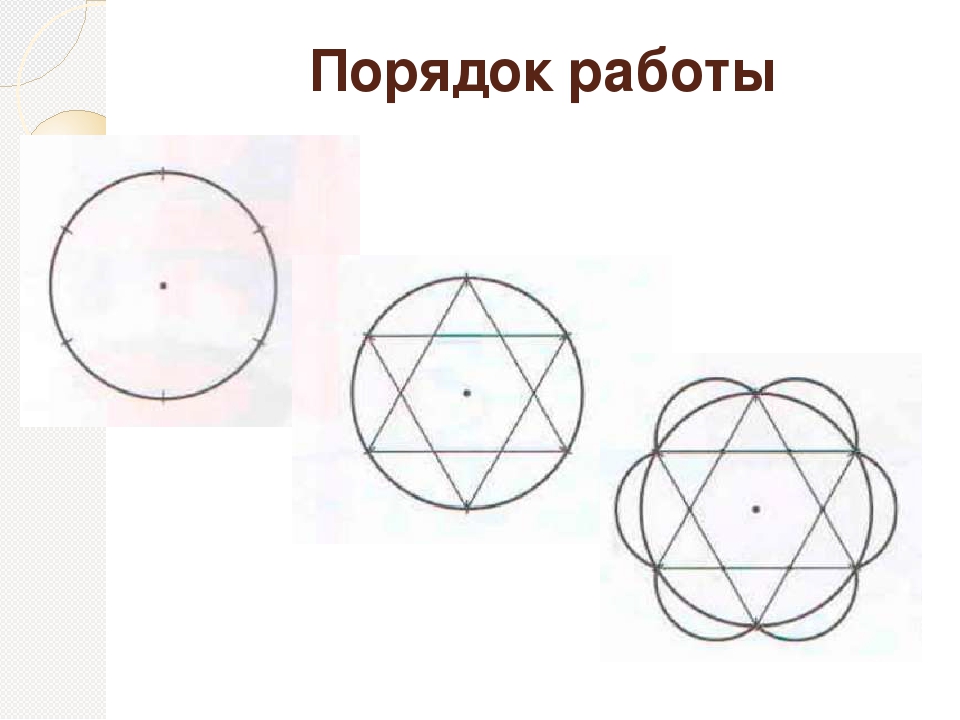 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.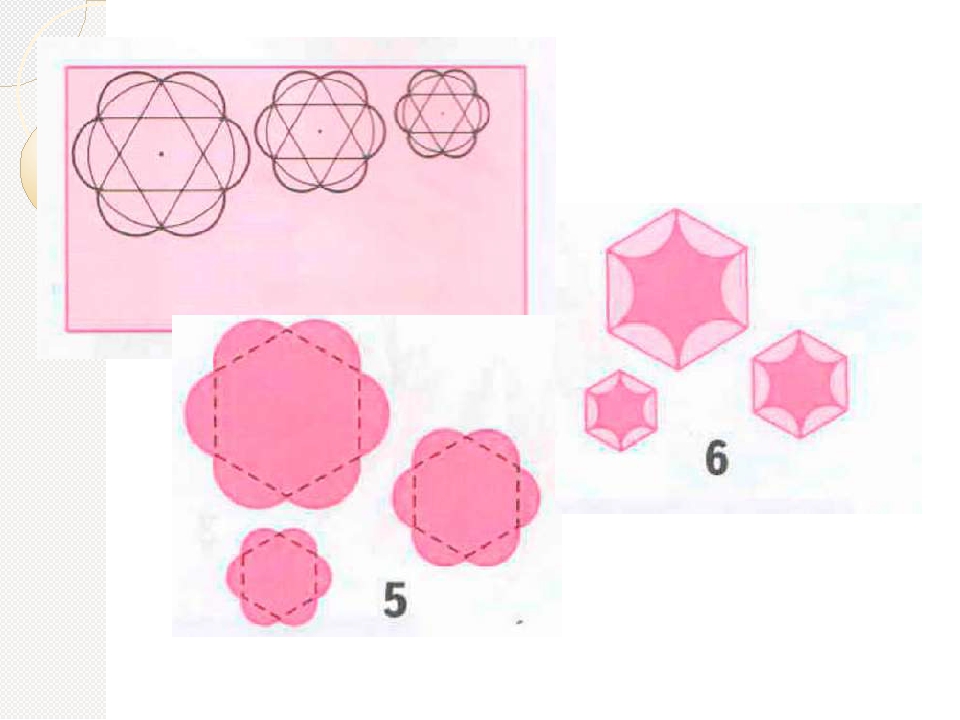

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.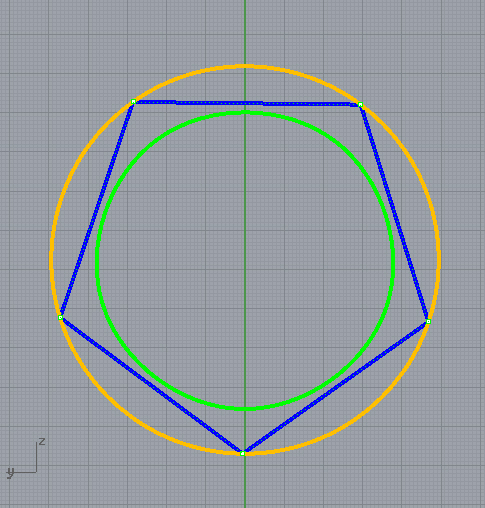

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В.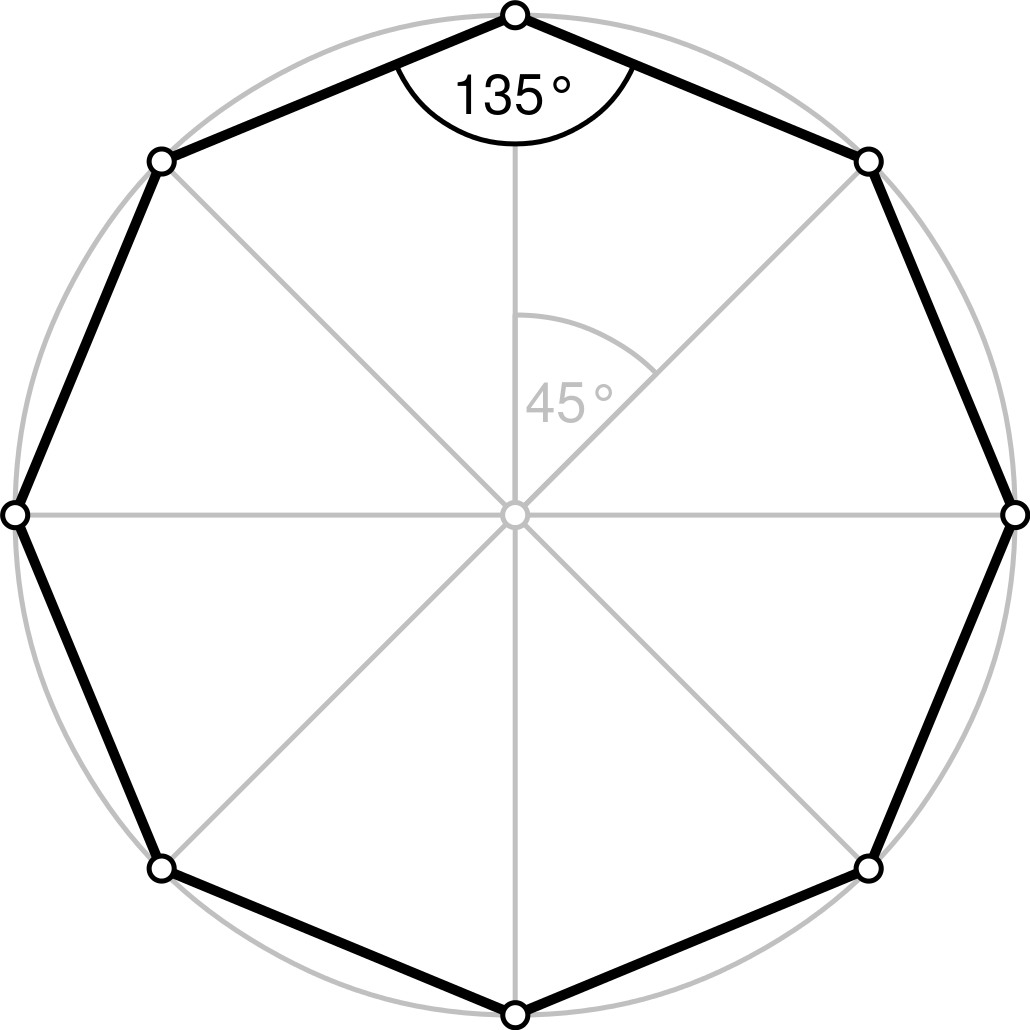 Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.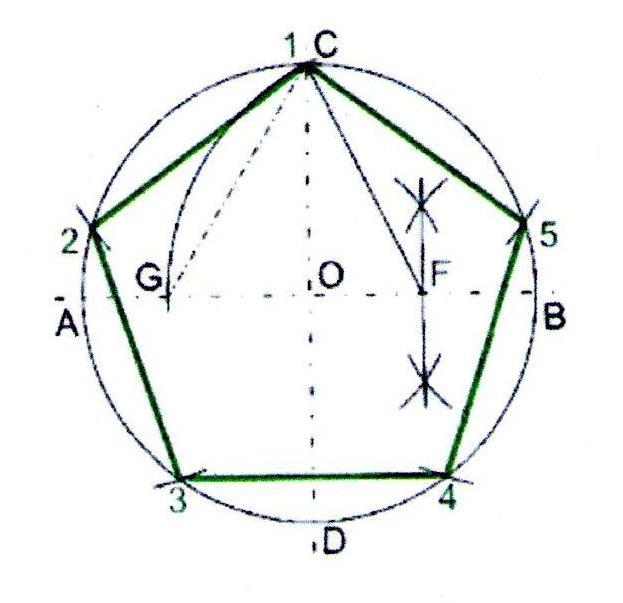

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Please enable cookies

This website is using a security service to protect itself from online attacks. The service requires full cookie support in order to view the website.

Please enable cookies on your browser and try again.

This website is using a security service to protect itself from online attacks.

This process is automatic, you will be redirected to the requested URL once the validation process is complete.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.

Вам понадобится

• Циркуль, линейка, карандаш, лист бумаги.

Инструкция

1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.

2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.

3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.

Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.

Вам понадобится

• Карандаш, лист бумаги, линейка

Инструкция

1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.

2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.

Видео по теме

Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.

Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкция

1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)

2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)

Видео по теме

Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.

Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.

Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.

Вам понадобится

• транспортир, угольник, циркуль, линейка

Инструкция

1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.

2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.

3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.

4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.

5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.

6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.

Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.

Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.

Вам понадобится

Инструкция

1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.

2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.

3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.

4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.

5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).

6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.

7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).

Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.

При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.

Инструкция

1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.

2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.

3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.

4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.

5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.

6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.

Видео по теме

Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.

Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.

Как вписать шестигранник в окружность

Popular

Основы черчения

Строительное

Машиностроительное

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.

Вам понадобится

• Циркуль, линейка, карандаш, лист бумаги.

Инструкция

1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.

2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.

3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.

Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.

Вам понадобится

• Карандаш, лист бумаги, линейка

Инструкция

1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.

2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.

Видео по теме

Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.

Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкция

1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)

2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)

Видео по теме

Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.

Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.

Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.

Вам понадобится

• транспортир, угольник, циркуль, линейка

Инструкция

1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.

2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.

3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.

4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.

5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.

6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.

Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.

Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.

Вам понадобится

Инструкция

1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.

2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.

3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.

4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.

5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).

6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.

7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).

Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.

При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.

Инструкция

1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.

2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.

3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.

4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.

5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.

6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.

Видео по теме

Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.

Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Способ вычерчивания шестиугольника циркулем, линейкой

Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.

Метод выглядит следующим образом:

Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

• циркулем вычерчивается окружность — радиус является размером стороны;
• по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
• находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
• находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.

Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.

Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

• к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
• на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
• операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
• разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
• уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
• строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
• контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

• после вычерчивания центрального отрезка по нему выравнивается рейсшина;
• инструмент откатывается вниз на произвольную величину;
• короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
• скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Правильный шестиугольник – это многоугольник, состоящий из шести равных сторон. Все соседние стороны образуют угол 120°.

Формулы

• P – периметр
• S – площадь
• R – радиус K
• r – радиус k

• S’ – центр
• a – сторона
• K – окружность описанная
• k – окружность вписанная

При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.

Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.

Как нарисовать шестиугольник с помощью циркуля

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >

Нам понадобятся: карандаш, линейка, циркуль.

Построение угла в 60

1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

1. Построим угол 60, кака описано выше.

2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

Построение угла в 90

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

Разделение отрезка на равные части.

1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

Построение правильного пятиугольника.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .

Построение правильного шестиугольника.

1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

Построение правильного семиугольника.

1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G .

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .

Общий метод построения многоугольников.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…

Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…

Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…

Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, п

Как построить правильный шестиугольник по одной стороне с помощью циркуля и линейки или линейки

Как построить правильный шестиугольник учитывая одну сторону. Строительство начинается с нахождения центра шестиугольника, а затем его рисования. описанный круг это круг, который проходит через каждый вершина. Затем компас обходит круг, отмеченный с каждой стороны.

Пошаговые инструкции для печати

Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.

Объяснение метода

Эта конструкция очень похожа на построение шестиугольника, вписанного в круг, за исключением того, что нам дан не круг, а одна из сторон. Шаги 1-3 нужны, чтобы нарисовать этот круг, и с тех пор конструкции такие же.

Центр круга находится с использованием того факта, что радиус правильного шестиугольника (расстояние от центра до вершины) равна длине каждой стороны. См. Определение шестиугольника.

Проба

Изображение ниже — это последний рисунок из приведенной выше анимации.

	Аргумент	Причина
1	ABCDEF — шестигранник	Это многоугольник с шестью сторонами. См. Определение шестиугольника.
2	AB, BC, CD, DE, EF, FA все совпадают.	Нарисовано с той же шириной компаса AF.
3	A, B, C, D, E, F все лежат на окружности O	По конструкции
4	ABCDEF — правильный шестиугольник	Из (1), (2).Все его вершины лежат на окружности, а все стороны равны. Это определяет правильный шестиугольник. Увидеть Определение и свойства правильного многоугольника

— Q.E.D

Попробуйте сами

Щелкните здесь, чтобы распечатать лист с двумя проблемами, которые можно попробовать. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.

Другие конструкции, страницы на сайте

Строки

Уголки

Треугольники

Правые треугольники

Центры треугольника

Окружности, дуги и эллипсы

Полигоны

Неевклидовы конструкции

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Площадь круга, вписанного в правильный шестиугольник

Для правильного шестиугольника с длиной стороны a задача состоит в том, чтобы найти площадь вписанной в него окружности, учитывая, что окружность касается каждой из шести сторон.

Примеры:

Ввод: a = 4
Выход: 37,68

Ввод: a = 10
Выход: 235,5
 

Подход :
Из рисунка видно, что мы можем разделить правильный шестиугольник на 6 одинаковых равносторонних треугольников.
Возьмем один треугольник OAB , с O в качестве центра шестиугольника или круга и AB в качестве одной стороны шестиугольника. 2/4

Ниже представлена ​​реализация подхода :

C ++

# включить <бит / stdc ++.ч> с использованием пространства имен std; поплавок круговая площадь ( поплавок a) { если (a <0) возврат -1; с плавающей запятой A = (3.14 * 3 * pow (а, 2)) / 4; возврат A; } внутренний основной () { с плавающей запятой a = 4; cout << circlearea (a) << endl; возврат 0; }

Java

импорт java.util. *; класс раствор { статический двойной круговая площадь ( двойной a) { если (a < 0 ) возврат - 1 ; двойной A = ( 3.14 * 3 * Math.pow (a, 2

Почему соты имеют шестиугольную форму?

Медоносные пчелы со временем эволюционировали, чтобы умело строить шестиугольные соты. Шестиугольник - подходящая форма для хранения меда? Могут ли другие формы, такие как круги, треугольники или квадраты, работать так же хорошо?

Давайте исследуем этот вопрос, сначала сделав несколько наблюдений за сотами. Мы возьмем макро, или широкую перспективу, чтобы изучить общий вид сот.Затем мы увеличим масштаб для микро- или крупного плана, чтобы рассмотреть конкретные детали.

С точки зрения макроса, что вы, , наблюдаете о форме сотовых ячеек?

Shutterstock

Издалека клетки могут казаться круглыми, как если бы они были построены так, чтобы соответствовать удлиненной форме тела пчелы.

А теперь давайте посмотрим на клетки и сфокусируемся на них.

Какие новые подробности сотовых ячеек вы заметили с точки зрения микроэлементов?

Shutterstock

Вы обратили внимание на шестиугольную форму ячеек?

Ученые используют свои наблюдения, чтобы понять мир, в котором мы живем.Когда ученые сталкиваются с явлением и озадачены тем, что они наблюдают, например шестиугольной формой сотовой ячейки, они часто задают вопросы и пытаются понять явление, формируя «заявление».

Вы сделали несколько наблюдений за сотовыми ячейками. Сформулируем утверждение о форме этих ячеек.

Научное утверждение. . .

• отвечает на научный вопрос или проблему и обычно представляет собой утверждение или понимание явления.
• всегда подтверждается научными данными или «доказательствами».
• предоставляет «рассуждение» или оправдание, которое логически связывает доказательства с заявлением. Обычно он основан на научном определении, законе, правиле или принципе.
• может быть пересмотрен по мере сбора дополнительных доказательств и / или установления логических связей, поддерживающих изменения в рассуждениях.

Создано Xochitl Garcia

Мы часто называем процесс разработки и объяснения претензии «CER» для C laim, E vidence и R easoning.

Почему пчелы используют шестиугольные формы для создания сот?

На основе ваших наблюдений за сотами используйте рабочий лист CER, чтобы заявить, почему вы думаете, что клетки имеют форму шестиугольников.

Рабочие листы для учащихся и ресурсы для преподавателей см. В «Наборе инструментов для преподавателя».

Соты изготавливаются из пчелиного воска, вещества, производимого рабочими пчелами. При правильной температуре рабочие пчелы выделяют восковые чешуйки из специальных желез в своем теле.Затем они жуют воск с небольшим количеством меда и пыльцы, чтобы произвести пчелиный воск. Гексагональные ячейки служат емкостями для хранения меда, а также домами для выращивания молодых пчел.

Пчелы выделяют воск из специальных желез в брюшке. Иллюстрация Корлетта Дугласа

Пчелы должны эффективно строить соты.

Иллюстрация Корлетта Дугласа

Пчелы собирают нектар и пыльцу с цветов, чтобы сделать мед, сладкую пищу для колонии. Мед дает пчелам энергию, необходимую им для выживания и размножения, а также для строительства домов.Чтобы произвести достаточно воска, рабочие пчелы нуждаются в большом количестве энергии и, следовательно, должны потреблять много меда. По оценкам некоторых исследований, пчелы должны потреблять восемь унций меда на каждую унцию производимого воска. Представьте, сколько цветов должна посетить пчела, чтобы превратить нектар в восемь унций меда!

В среднем каждая пчела может произвести около 1/12 чайной ложки меда за свою жизнь. Если пчела даст один фунт меда, ей потребуется около 2 миллионов цветов. За свою жизнь целая колония может преодолеть около 55 000 миль!

Иллюстрация Корлетта Дугласа

Производство воска - тяжелая работа.

Каким будет соотношение потребляемого меда к произведенному воску? Измерьте воду в мерном цилиндре (30 мл = 1 унция), чтобы увидеть соотношение.

• Отмерьте 8 унций «меда» (вода окрашена в медовый цвет).
• Отмерьте 1 унцию «воска» (обычная вода).

Сравните количество меда и воска.

Почему пчелы делают шестиугольники? | Спросите доктора Вселенная

Уважаемый Адитья,

Когда пчелы строят в своих ульях шестиугольники, шестигранные формы идеально подходят друг другу.На самом деле, мы никогда не видели, чтобы пчелы могли принимать какую-либо другую форму. Это то, что я узнал, когда навестил свою подругу Сью Коби, исследовательницу пчел из Университета штата Вашингтон.

Коби показал мне соты, в которых живут и работают самки пчел. Шестиугольники - полезные формы. Они могут содержать яйца пчелиной матки и хранить пыльцу и мед, которые рабочие пчелы приносят в улей.

Если подумать, создание кругов не слишком хорошо работает. В сотах останутся зазоры. Рабочие пчелы могли использовать для хранения треугольники или квадраты.Это не оставит пробелов. Но шестиугольник - самая прочная и полезная форма.

Не спрашивайте пчел. Коби объяснил, что люди недавно использовали математику, чтобы выяснить, почему шестиугольники имеют наибольший смысл.

«Геометрия этой формы использует наименьшее количество материала для удержания наибольшего веса», - сказала она.

Чтобы сделать соты, пчелам потребуется немало усилий. Воск поступает из желез на животе или брюшке пчел. Чтобы сделать одну унцию воска, пчелы должны приготовить и съесть около двух столовых ложек меда.Затем они могут добавлять этот воск в расческу по мере наращивания. По словам Коби, пчелиная семья может произвести 100 фунтов меда. В некоторых местах они могут даже принести от 300 до 500 фунтов. Структура важна, чтобы удерживать весь этот вес и защищать мед, особенно зимой.

Шестиугольник может сэкономить пчелам время и энергию. Они могут использовать энергию для выполнения еще одной очень важной работы: переносить пыльцу с цветка на цветок, что позволяет расти новым растениям. У меня кошачий инстинкт ударить пчелу, но я стараюсь этого не делать, потому что пчелы очень важны.Они позволяют нам есть пищу.

«Медоносная пчела - удивительное животное, с которым действительно интересно работать», - сказал Коби. «И она отвечает за опыление ваших фруктов, овощей и орехов».

Прочный и удобный улей может помочь пчелам выполнять свою работу.

Не так давно некоторые ученые задавались вопросом, как именно пчелы строят эти шестиугольники. Они обнаружили, что некоторые пчелы начинают делать круги в воске, используя свое тело в качестве инструмента. Ученые не знают, почему это происходит, но пчелы, похоже, используют тепло своего тела, чтобы плавить воск из формы круга в форму шестиугольника.

Шестиугольники и соты также полезны для создания вещей, которыми пользуются люди, например мостов, самолетов и автомобилей. Это придает материалам дополнительную прочность.

В конце концов, материалы шестиугольной формы также могут выдерживать большую нагрузку, даже если они сделаны из более легкого материала. Это то, что я узнал от моего друга Пичжун Циоа, инженера и профессора WSU.

«Мы узнали это от пчелы», - сказал он. «Шестиугольники применимы практически ко всему, что вы можете построить».

Из-за того, что пчелы ни разу в жизни не выполняли домашнее задание по математике, похоже, что они используют творческую геометрию и инженерные решения для строительства своей штаб-квартиры.

С уважением,

Доктор Вселенная

П.С. Здесь вы можете найти свой собственный путеводитель по пчеловодству.

Никогда не пропустите вопросы и ответы от Dr. Universe и друзей. Подпишитесь на нашу рассылку новостей:

Урок 1: Как рисовать

Щелкните здесь, чтобы прочитать введение к курсу, если вы его пропустили!

Рисование - это просто процесс наложения фигур, линий, каракулей и значений друг на друга до тех пор, пока вы не получите желаемый результат.

В этом первом уроке мы сосредоточимся на процессе создания эскиза . Если вы можете сделать отметку на листе бумаги, вы сможете научиться рисовать! Чтобы стать художником, необязательно уметь рисовать прямые линии или идеальные круги.

Введение в создание эскиза

Набросок - это процесс наброска идеи на бумаге. Это позволяет быстро воплотить ваши идеи в жизнь, что в конечном итоге сэкономит время. Это отличный способ провести мозговой штурм!

Самое замечательное в эскизах то, что они обычно сливаются или исчезают, пока вы продолжаете развивать концепцию своего рисунка.

Так что не бойтесь ошибаться!

Эта стадия предназначена для разведки! Когда я делаю ошибку, я нахожу способы использовать ее в своих интересах. Если не получится, я просто пойду дальше.

Можете ли вы сказать, что этот набросок был создан с использованием одного из приведенных выше эскизов?

Как сделать набросок

Лучше всего использовать плавные линии, которые нарисованы свободно и легко. Для этого отрегулируйте хватку карандаша так, чтобы ваша рука была расслабленной, а не напряженной.Если ваша рука обычно устает после того, как вы рисовали менее часа, вероятно, вы сжимаете ее слишком сильно.

Ничего страшного, если ваши линии шатаются, потому что вы еще не привыкли рисовать определенные линии и кривые. Рисование сильно отличается от письма, поэтому вам нужно улучшать мышечную память, рисуя как можно чаще!

При создании начального наброска вам нужно отказаться от перфекционизма и сосредоточиться на общих формах. Подумайте о размере, форме, угле и т. Д.Последнее, о чем вы хотите думать, - это детали!

Нарисуем что-нибудь вместе!

Поскольку это руководство по рисованию для начинающих, я использую свою левую руку (недоминантная рука), чтобы показать вам, что вам не нужно хорошо контролировать свою руку, чтобы рисовать хорошо.

Шаг 1: Нарисуйте свободный круг

Мои линии такие шаткие!

Я нарисовал круг, используя набор слабо проведенных линий. Не волнуйтесь, если ваши реплики идут в странном направлении.Скорее всего, вы не собираетесь нарисовать что-то идеальное с первого раза. Совершенно нормально! Помните, мы должны работать слоями.

Шаг 2: Уточните форму

После начального наброска найдите области, требующие улучшения, и зарисуйте их, пока не приблизитесь к желаемому результату.

Шаг 3: Продолжайте уточнять

Продолжайте повторять этот шаг, пока не приблизитесь к тому, что вы хотите.

Совет. Вы можете повернуть альбом для рисования, чтобы глаза смотрели на фигуру по-другому.Вы можете заметить некоторые очевидные области, которые нужно исправить.

Шаг 4. Определите форму

Довольны тем, как она выглядит в целом? Используйте более уверенные линии, чтобы определить форму вашего круга. Вы можете стереть нарисованные линии или позволить им исчезнуть естественным образом, продолжая работать над рисунком.

Как этот пример? Вот еще немного!

После рисования всех этих и многих других примеров с использованием моей недоминантной руки я заметил некоторые большие улучшения!

Я привык двигать локтем и плечевым суставом для рисования, что давало мне гораздо более плавные линии.Если вы посмотрите на изображения в примере выше, вы заметите, что мои линии постепенно становятся менее шаткими.

Я подумал, что было бы забавно показать вам разницу между наброском, сделанным моей левой и правой рукой:

Опять же, вам не нужно хорошо рисовать прямые линии или отлично владеть карандашом. чтобы уметь рисовать. Хороший контроль означает, что ваш рисунок будет выглядеть чище и, в свою очередь, более точным.

Домашнее задание

Что нужно помнить во время рисования:

1. Не будьте перфекционистом
2. Сосредоточьтесь на общей форме, а не на деталях
3. Используйте небольшое давление

Assignment # 1:

Заполните всю страницу в альбоме, следуя инструкциям этого урока.

Шаг 1: Нарисуйте произвольно

Шаг 2: Уточните форму

Шаг 3: Уточните его еще

Шаг 4: Определите желаемую форму

Найдите объекты для рисования вокруг дома, снаружи или с помощью быстрого поиска в Google «Случайные объекты». После того, как вы заполните всю страницу в своем альбоме, заполните еще одну.

Моя задача для вас: если вы можете нарисовать 50 вещей в своем альбоме для рисования и отправить их на страницу facebook, я покажу вам ваши работы внизу!

Вот несколько идей для рисования:

1. Вилка
2. Apple
3. Банан
4. Ноутбук
5. Куртка
6. Шляпа
7. Твоя рука
8. Твоя ступня
9. Твой глаз
10. Ключ лампы
Кошка
11. Собака
12. Птица
13. Лодка
14. Дерево
15. Цветок
16. Автомобиль
17. Вертолет
18. Самолет
19. Аллигатор
20. Человек в прыжке
21. Человек в прыжке
22. Лицо на ноге
3 Выполнено задание?

Сообщите мне, улучшились ли вы и как этот урок помог вам лучше рисовать!

Если вы ждете урока 2, подпишитесь на мой специальный список рассылки на боковой панели или подпишитесь на меня в facebook, и я сообщу вам, когда он будет опубликован.

Обновление: Щелкните здесь, чтобы перейти к уроку 2

Есть вопросы? Оставьте их в разделе комментариев ниже, и я скоро к вам вернусь!

Читатели, выполнившие задание!

Памела Гейл Роуэлл

Фироз Вадуд <- он нарисовал 80 !!

Крис Браун

ShinChan

Найкеша Гуинита

Анахита Шарма

000

000

000

000

000 Гилен Антуан

Как физика придает структуру природе

Как это делают пчелы? Соты, в которых они хранят свой янтарный нектар, - это чудо точной инженерии, массив ячеек в форме призмы с идеально шестиугольным поперечным сечением.Восковые стенки имеют очень точную толщину, ячейки слегка наклонены от горизонтали, чтобы предотвратить вытекание вязкого меда, а вся соты выровнены по магнитному полю Земли. Тем не менее, эта структура создается без какого-либо плана или предвидения, когда многие пчелы работают одновременно и каким-то образом координируют свои усилия, чтобы избежать несовпадения клеток.

Древнегреческий философ Папп Александрийский считал, что пчелы должны быть наделены «определенной геометрической предусмотрительностью.«И кто мог дать им эту мудрость, кроме Бога? По словам Уильяма Кирби в 1852 году, пчелы - это «математики с небесами». Чарльз Дарвин не был так уверен, и он провел эксперименты, чтобы установить, могут ли пчелы строить идеальные соты, используя только развитые и унаследованные инстинкты, как предполагала его теория эволюции.

СИЛЫ В РАБОТЕ: Пчелы, кажется, развили способность делать идеально шестиугольные клетки из мягкого воска, который они выделяют. Однако некоторые исследователи полагают, что поверхностного натяжения в мягком воске может быть достаточно, чтобы придать клеткам форму, почти так же, как он организует пузыри в пузырчатой ​​пластине.Grafissimo / Getty

Но почему шестиугольники? Это простой вопрос геометрии. Если вы хотите упаковать ячейки, одинаковые по форме и размеру, чтобы они заполняли всю плоскую плоскость, подойдут только три правильные формы (со всеми сторонами и углами): равносторонние треугольники, квадраты и шестиугольники. Из них шестиугольные ячейки требуют наименьшей общей длины стены по сравнению с треугольниками или квадратами той же площади. Поэтому разумно, что пчелы выберут шестиугольники, поскольку изготовление воска требует затрат энергии, и они захотят использовать как можно меньше - так же, как строители могут захотеть сэкономить на стоимости кирпичей.Это поняли в XVIII веке, и Дарвин заявил, что шестиугольные соты «абсолютно идеальны с точки зрения экономии труда и воска».

Дарвин считал, что естественный отбор наделил пчел инстинктом для создания этих восковых камер, преимущество которых заключалось в том, что они требовали меньше энергии и времени, чем те, которые имели другие формы. Но даже несмотря на то, что пчелы, кажется, обладают специальными способностями к измерению углов и толщины стенок, не все согласны с тем, насколько они должны полагаться на них.Это потому, что создание гексагональных массивов ячеек - это то, чем природа все равно занимается.

УСТАНОВКА: Один слой или «плот» пузырьков содержит в основном шестиугольные пузырьки, хотя не все из них являются идеальными шестиугольниками. Есть некоторые «дефекты» - пузыри с пятью или семью сторонами. Тем не менее, все стыки стенок пузыря тройные, пересекающиеся под углами, близкими к 120 градусам. Шебеко / Shutterstock Также по физике

Гениальное: Алан Лайтман

Майкл Сигал

Алан Лайтман ждал меня у почтового отделения в маленьком городке штата Мэн.«Я не смогу сказать ничего достаточно интересного, - сказал он мне, пожав мне руку, - чтобы оправдать ваш приезд сюда». И то и другое было ... ПОДРОБНЕЕ

Если вы надуваете слой пузырьков на поверхности воды - так называемый «плот с пузырьками» - пузырьки становятся шестиугольными или почти таковыми. Вы никогда не найдете плот из квадратных пузырей: если четыре стенки пузыря сходятся вместе, они мгновенно трансформируются в соединения из трех стенок с более или менее равными углами в 120 градусов между ними, как в центре символа Mercedes-Benz.

Очевидно, нет агентов, которые формируют эти плоты, как пчелы со своими сотами. Все, что руководит закономерностью, - это законы физики. У этих законов, очевидно, есть определенные предпочтения, такие как смещение в сторону трехстороннего соединения стенок пузыря. То же самое и с более сложными пенами. Если вы складываете пузырьки в трех измерениях, продувая соломинку в таз с мыльной водой, вы увидите, что, когда стенки пузыря встречаются в вершине, это всегда четырехстороннее соединение с углами между пересекающимися пленками, примерно равными примерно 109 градусы - угол, относящийся к четырехгранному геометрическому тетраэдру.

BUBBLE VISION: Сложные глаза насекомых упакованы гексагонально, как пузыри на плоту пузырей, хотя на самом деле каждая грань представляет собой линзу, соединенную с длинной тонкой клеткой сетчатки. Структуры, которые образованы кластерами биологических клеток, часто имеют формы, управляемые во многом теми же правилами, что и пена и пузырчатые плотики - например, всего три клеточные стенки встречаются в любой вершине. Микроскопическая структура фасеток глаза мухи - помимо того, что здесь видно - является одним из лучших примеров.Каждая грань содержит кластер из четырех светочувствительных ячеек, которые имеют ту же форму, что и кластер из четырех обычных пузырьков. Tomatito / Shutterstock

Что определяет эти правила соединения мыльной пленки и формы пузырьков? Природа заботится об экономии даже больше, чем пчелы. Пузырьки и мыльные пленки состоят из воды (с оболочкой из молекул мыла), а поверхностное натяжение на поверхности жидкости дает ей как можно меньшую площадь. Вот почему капли дождя имеют сферическую (более или менее) форму при падении: сфера имеет меньшую площадь поверхности, чем любая другая форма с таким же объемом.По той же причине на восковом листе капли воды собираются в маленькие бусинки.

Это поверхностное натяжение объясняет структуру пузырьков и пен. Пена будет стремиться найти структуру с наименьшим общим поверхностным натяжением, что означает наименьшую площадь стены из мыльной пленки. Но конфигурация пузырьковых стен также должна быть механически стабильной: буксиры в разных направлениях на стыке должны идеально уравновешиваться, так же как силы должны быть уравновешены в стенах собора, если здание собирается устоять.Трехстороннее соединение в пузырчатой ​​пластине и четырехстороннее соединение в пене - это конфигурации, которые обеспечивают этот баланс.

Но те, кто думают (как и некоторые), что соты - это просто затвердевший пузырчатый плот из мягкого воска, могут затруднить объяснение того, как такой же шестиугольный массив клеток встречается в гнездах бумажных ос, которые строят не из воска, а из пережеванные комки волокнистой древесины и стебли растений, из которых они делают своего рода бумагу. Поверхностное натяжение здесь не только мало влияет, но также кажется очевидным, что разные типы ос имеют разные унаследованные инстинкты в отношении их архитектурного дизайна, которые могут значительно отличаться от одного вида к другому.

ФОРМИРОВАНИЕ КАПЛИ: Когда вода попадает на водоотталкивающую поверхность, она может распадаться на капли. Форма этих капель определяется поверхностным натяжением, которое придает им примерно сферическую форму, а также силой тяжести (которая сглаживает каплю на горизонтальной поверхности) и силами, действующими между водой и подстилающей твердой поверхностью. Если эти последние силы достаточно сильны, капли превращаются в блины в форме линз. А если поверхность не обладает сильными водоотталкивающими свойствами, капли могут растекаться в плоскую гладкую пленку.Слева вверху: Стучелова, Куттельвасерова / Shutterstock; Вверху справа: Ольгиша / Shutterstock; Внизу: Pitiya Phinjongsakundit / Shutterstock

Хотя геометрия стыков мыльной пленки и продиктована взаимодействием механических сил, она не сообщает нам, какой будет форма пены. Типичная пена содержит многогранные ячейки самых разных форм и размеров. Присмотритесь, и вы увидите, что их края редко бывают идеально прямыми; они немного изогнуты. Это связано с тем, что давление газа внутри ячейки или пузыря увеличивается по мере того, как пузырек становится меньше, поэтому стенка маленького пузыря рядом с большим пузырем будет слегка выпирать наружу.Более того, некоторые грани имеют пять сторон, другие шесть, а некоторые всего четыре или даже три. При небольшом изгибе стенок все эти формы могут получить четырехсторонние соединения, близкие к «четырехгранной» конфигурации, необходимой для механической устойчивости. Таким образом, формы ячеек обладают некоторой гибкостью (буквально). Пены, хотя и подчиняются геометрическим правилам, довольно беспорядочные.

Предположим, что вы можете сделать «идеальную» пену, в которой все пузырьки имеют одинаковый размер. Какова же тогда идеальная форма ячейки, при которой общая площадь стенок пузыря должна быть как можно меньше, а требования к углам стыков удовлетворяются? Это обсуждалось в течение многих лет, и долгое время считалось, что идеальной формой ячейки является 14-гранный многогранник с квадратными и шестиугольными гранями.Но в 1993 году была обнаружена несколько более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми различных форм ячеек. Этот более сложный узор послужил источником вдохновения для пенистого дизайна плавательного стадиона Олимпийских игр 2008 года в Пекине.

Правила формы ячеек в пеноматериалах также управляют некоторыми узорами, наблюдаемыми в живых клетках. Мало того, что сложный глаз мухи демонстрирует ту же шестиугольную упаковку граней, что и плот с пузырями, но и светочувствительные клетки в каждой из отдельных линз также сгруппированы в группы по четыре, которые выглядят так же, как мыльные пузыри.У мутантных мух с более чем четырьмя такими клетками в кластере расположение также более или менее идентично тому, которое было бы у пузырей.

ИСПОЛЬЗОВАНИЕ ПУЗЫРЬКОВ: Пузырьки и пена используются в природе. Здесь обыкновенная пурпурная улитка висит на поверхности моря с плавучего плота, сделанного из пузырей, покрытых слизью. Это позволяет улитке питаться маленькими существами, живущими на поверхности воды. Дорлинг Киндерсли

Из-за поверхностного натяжения мыльная пленка, натянутая на проволочную петлю, растягивается, как упругая мембрана батута.Если проволочный каркас изгибается, пленка также изгибается с элегантным контуром, который автоматически подсказывает вам наиболее экономичный с точки зрения материала способ закрыть пространство, ограниченное рамкой. Это может показать архитектору, как сделать крышу сложной конструкции, используя наименьшее количество материала. Однако во многом благодаря красоте и элегантности этих так называемых «минималистичных поверхностей», а также из-за их экономичности, такие архитекторы, как Фрей Отто, использовали их в своих зданиях.

Эти поверхности минимизируют не только их площадь поверхности, но и их общую кривизну.Чем круче изгиб, тем больше кривизна. Кривизна может быть положительной (выпуклости) или отрицательной (провалы, впадины и седла). Следовательно, криволинейная поверхность может иметь нулевую среднюю кривизну, пока положительные и отрицательные стороны компенсируют друг друга.

Таким образом, лист может иметь высокую кривизну, но при этом иметь очень маленькую или даже не иметь средней кривизны. Такая минимально изогнутая поверхность может разделить пространство на упорядоченный лабиринт проходов и каналов - сеть. Они называются периодическими минимальными поверхностями.(Периодичность просто означает структуру, которая идентично повторяется снова и снова, или, другими словами, регулярный образец.) Когда такие образцы были обнаружены в 19 веке, они казались просто математическим любопытством. Но теперь мы знаем, что природа их использует.

Клетки многих различных типов организмов, от растений до миног и крыс, содержат мембраны с подобными микроскопическими структурами. Никто не знает, для чего они нужны, но они настолько распространены, что справедливо предположить, что они играют какую-то полезную роль.Возможно, они изолируют один биохимический процесс от другого, избегая перекрестных помех и помех. Или, может быть, они просто эффективный способ создания большого количества «рабочей поверхности», поскольку многие биохимические процессы происходят на поверхности мембран, куда могут быть встроены ферменты и другие активные молекулы. Каким бы ни было его назначение, для создания такого лабиринта не нужны сложные генетические инструкции: законы физики сделают это за вас.

У некоторых бабочек, таких как европейская зеленая прическа и изумрудное сердце крупного рогатого скота, есть чешуйки крыльев, содержащие упорядоченный лабиринт из прочного материала, называемого хитином, в форме определенной периодической минимальной поверхности, называемой гироидом.Интерференция между световыми волнами, отражающимися от регулярных массивов гребней и других структур на поверхности масштаба крыла, приводит к исчезновению некоторых длин волн, то есть некоторых цветов, в то время как другие усиливают друг друга. Итак, здесь узоры служат средством создания цвета животных.

МИНЕРАЛЬНАЯ СЕТКА: Филигранные пористые скелеты губок, такие как эта цветочная корзина Венеры, представляют собой формы «замороженной пены», в которой минерал заливается вокруг стыков и пересечений пузырьковидных мягких тканей.Дмитрий Григорьев / Shutterstock

Скелет морского ежа Cidaris rugosa представляет собой пористую сетку, имеющую форму периодической минимальной поверхности другого типа. На самом деле это экзоскелет, расположенный вне мягких тканей организма, защитная оболочка, из которой вырастают опасно выглядящие шипы, сделанные из того же минерала, что и мел и мрамор. Открытая решетчатая структура означает, что материал прочный, но не слишком тяжелый, как пенопласт, используемый для строительства самолетов.

Чтобы создать упорядоченные сети из твердого жесткого минерала, эти организмы, очевидно, создают форму из мягких гибких мембран, а затем кристаллизуют твердый материал внутри одной из взаимопроникающих сетей.Другие существа могут создавать таким образом упорядоченную минеральную пену для более сложных целей. Из-за того, как свет отражается от элементов узорчатой ​​структуры, такие решетки могут действовать скорее как зеркала, ограничивая и направляя свет. Сотовое расположение полых микроскопических каналов в хитиновых шипах своеобразного морского червя, известного как морская мышь, превращает эти похожие на волосы структуры в естественные оптические волокна, которые могут направлять свет, заставляя существо менять цвет с красного на голубовато-зеленый в зависимости от направления движения. освещение.Это изменение цвета может служить отпугиванием хищников.

Этот принцип использования мягких тканей и мембран в качестве форм для формирования узорчатых минеральных экзоскелетов широко используется в море. У некоторых губок есть экзоскелеты, сделанные из минеральных стержней, связанных наподобие лазаных рам, которые очень похожи на узоры, образованные краями и стыками мыльных пленок в пене - не случайно, если поверхностное натяжение диктует архитектуру.

Такие процессы, известные как биоминерализация, дают впечатляющие результаты у морских организмов, называемых радиоляриями и диатомовыми водорослями.Некоторые из них имеют экзоскелеты с тонким рисунком, состоящие из сетки минеральных шестиугольников и пятиугольников: вы могли бы назвать их сотами моря. Когда немецкий биолог (и талантливый художник) Эрнст Геккель впервые увидел их формы в микроскоп в конце 19 века, он сделал их звездой привлекательности портфолио рисунков под названием Art Forms in Nature , которые оказали большое влияние на художников начала 20 века и до сих пор вызывают восхищение.

No related posts.