Инструкция

1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.

2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность.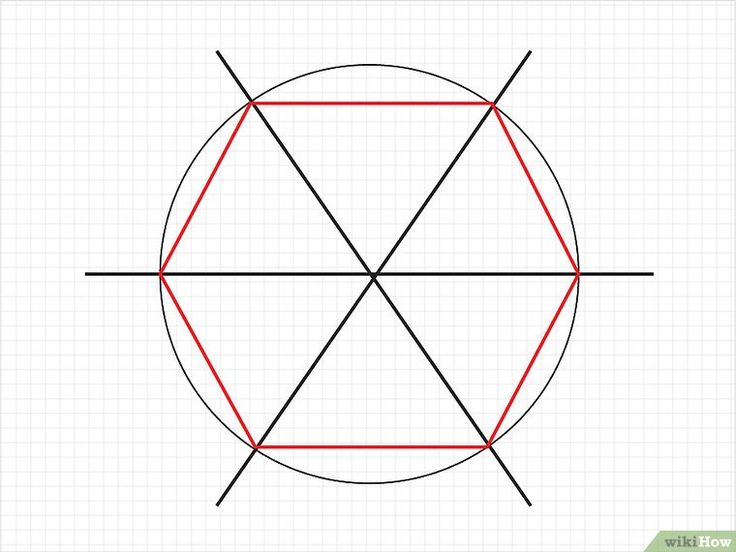 Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.

3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.

Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести.

Вам понадобится

• Карандаш, лист бумаги, линейка

Инструкция

1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.

2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.

Видео по теме

Обратите внимание!

Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкция

1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек.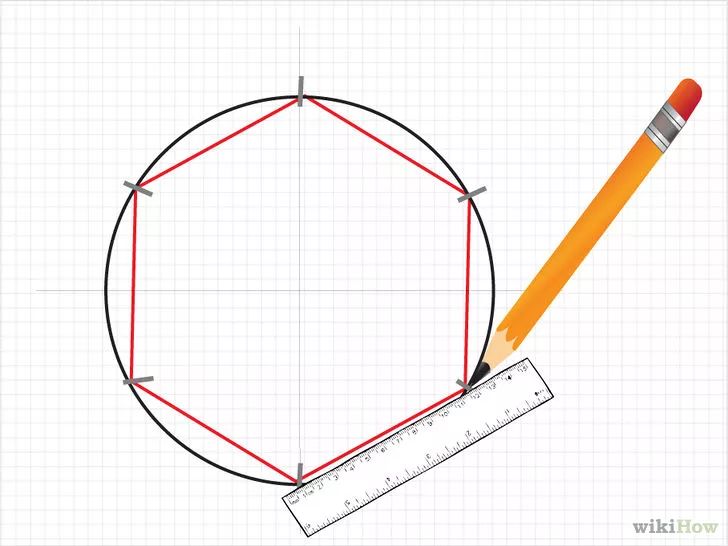 В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)

2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)

Видео по теме

Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.

Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.

Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.

Вам понадобится

• транспортир, угольник, циркуль, линейка

Инструкция

1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.

2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.

3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямо

4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой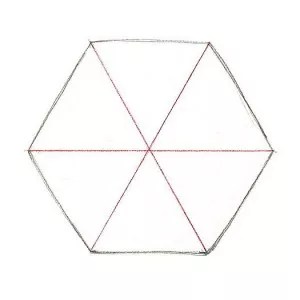

5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где

6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.

Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.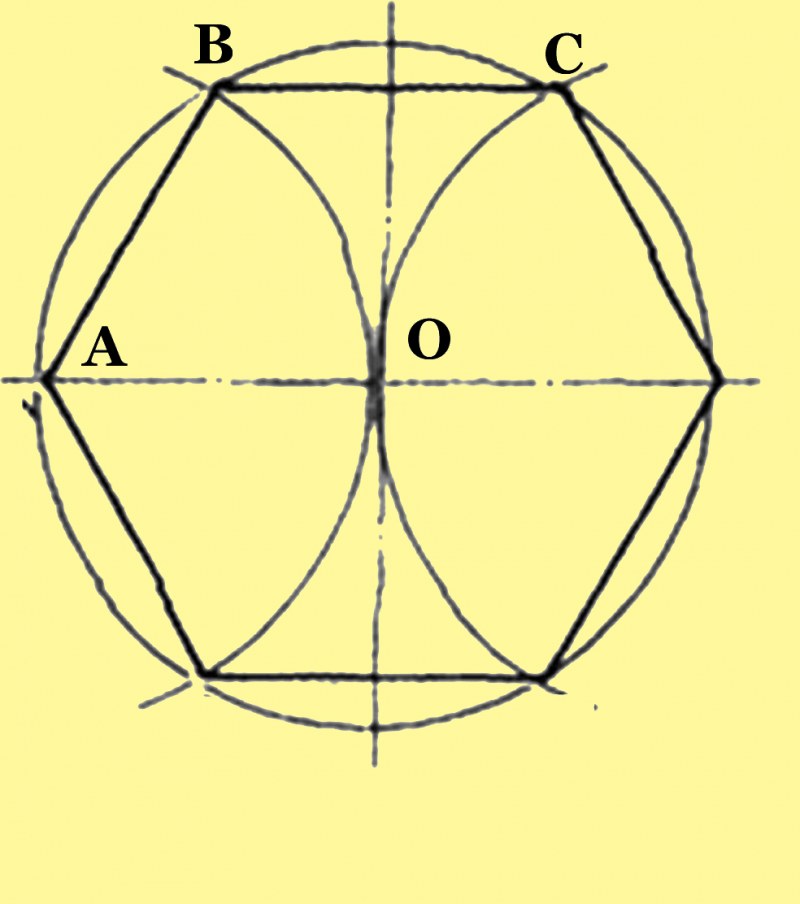

Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.

Вам понадобится

Инструкция

1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.

2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.

3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.

4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.

5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).

6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.

7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).

Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.

При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.

Инструкция

1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.

2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.

3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.

4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией.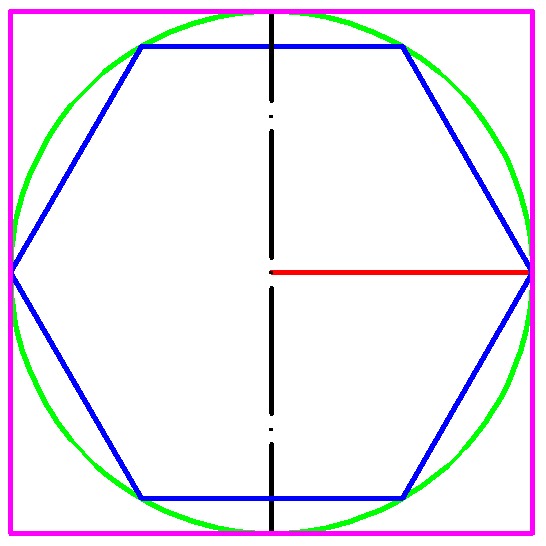 Получите треугол ьник АВС.

5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.

6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.

Видео по теме

Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.

Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.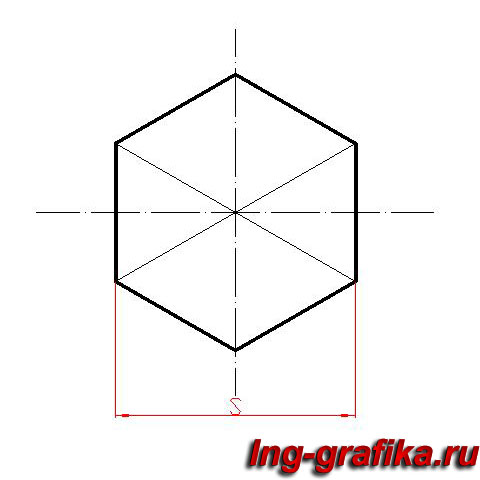

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…

Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…

Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…

Source: crast.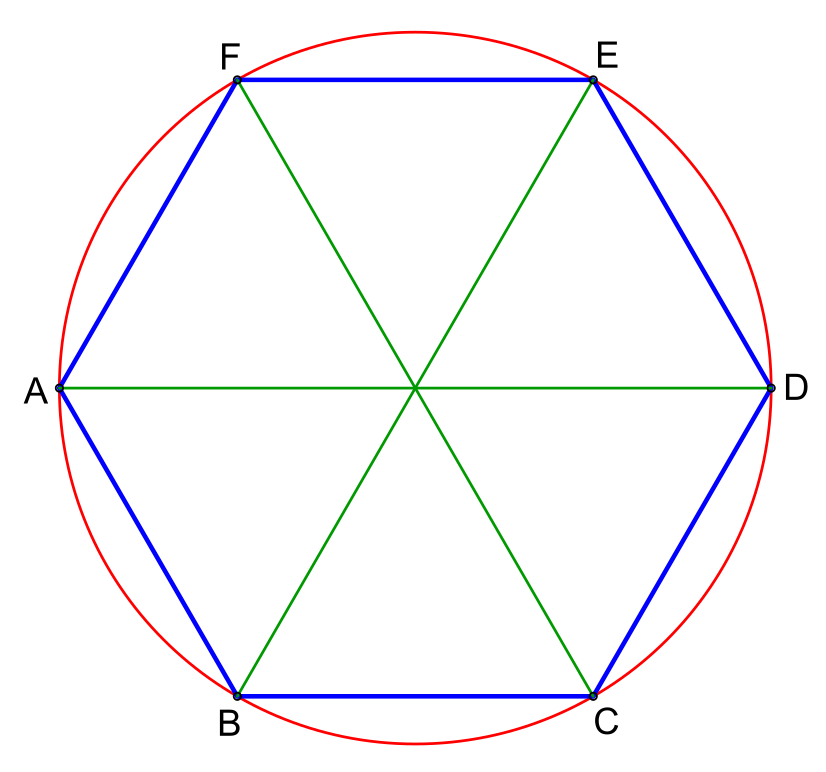 ru

Читайте также

Как нарисовать шестиугольник в линейной перспективе

Здравствуйте коллеги. В этом уроке узнаем, как нарисовать шестиугольник в перспективе.

Как вписать его фронтально в окружность мы смотрели в прошлом уроке. Заметьте ничего сложного нет. Нам удалось малыми средствами начертить равнобедренный предмет с шестью вершинами.

Его можно сделать еще проще. Например, отложить шесть радиусов на тело овала. Эта фигура не такая сложная, как с пятью или с семью углами, уроки которых мы рассмотрим в других статьях.

Я не фанат точной науки геометрии. Приходилось рисовать, но без циркуля и угольника не всегда получалось правильно создать картину.

Наша задача показать полную иллюзию пространства на двухмерной плоскости. Нарисуем многоугольник онлайн в перспективе, а для этого нужно знать правила построения.

К примеру, чтобы создать многоугольный узор на потолке, как на картине художника Премацци, нужно знать законы построения.

«Виды залов нового Эрмитажа. Галерея фламандской живописи.»

На картине Гау мы видим интерьер дворца. И все узоры выполнены в рамках законов линейной перспективы.

«Зимний дворец. Петровский зал.»

Посмотрите узор на полу в произведении Жерома Жан-Леона.

«Painting Breathes Life into Sculpture»

Задумывая сюжет в интерьере, нам придется изучать принципы построения.
Как положить шестигранник на плоскость посмотрите видео урок ниже.

Рисуем онлайн многоугольник в перспективе

Делал я его с помощью программы Photoshop, все то же самое можно сделать и на бумаге.
Для рисования нам понадобятся:

• Карандаш
• Циркуль
• Линейка
• Резинка

Такой небольшой набор инструментов необходим для черчения в живую.

Сам рисунок вы можете посмотреть на видео.

Сделаем акцент, когда шестиугольник вписанный в окружность.

Ниже на фото фигура построена. И, казалось бы, добавить нечего.

Но правильный рисунок будет если его вписать в овал. У нас есть две точки по сторонам квадрата, и появились новые четыре точки. Картинка ниже.

В таком формате он не будет деформированный, вытянутый или сплюснутый. На рисунке будет смотреться правдоподобнее.

По такому же принципу можно сделать фигуру не только горизонтально, но и вертикально.

В таком случае мы сможем выстроить призму. Для этого мы сделаем переднее и заднее основания и соединим их линиями. Эта процедура детально описана в моем платном курсе, можете перейти по этой ссылке.

Вот такой урок получился.
Творческих вам успехов.

Построение правильного шестигранника

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Читайте также:

Как проходит сварка.

Показатели температуры огня.

Способ вычерчивания шестиугольника циркулем, линейкой

Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.

Метод выглядит следующим образом:

Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 – углы, 0 – центр, D – радиус шестигранника.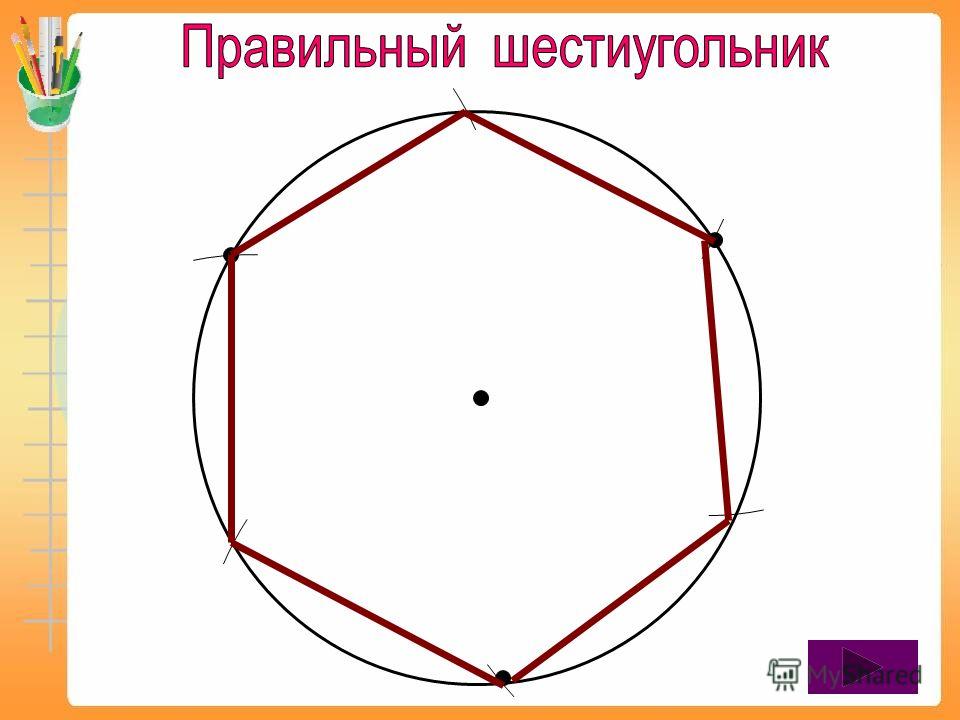

• циркулем вычерчивается окружность – радиус является размером стороны;
• по линейке проводится радиус – точки пересечения этого отрезка будут углами многоугольника;
• находятся два угла многоугольника – циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
• находятся оставшиеся два угла – циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.

Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.

Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.

Вернуться к оглавлению

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины – специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 – углы, 0 – центр, D – радиус шестигранника.

• к одной стороне отрезка прикладывается угольник – короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
• на листе/заготовке вычерчивается линия – длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
• операция повторяется при развороте угольника – угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
• разворот угольника – теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
• уточнение размеров сторон – на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
• строительство двух оставшихся сторон – они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
• контроль параллельности – шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a – диаметр, b – сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

• после вычерчивания центрального отрезка по нему выравнивается рейсшина;
• инструмент откатывается вниз на произвольную величину;
• короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
• скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.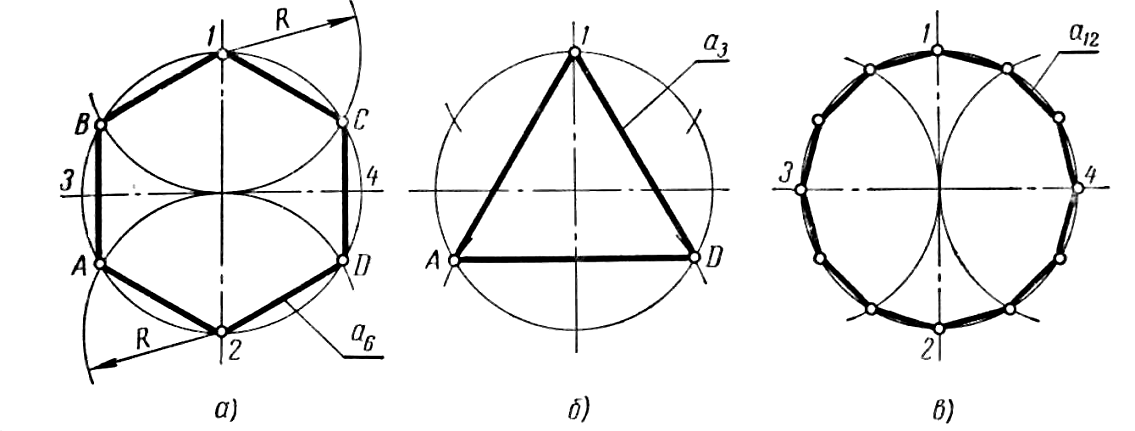

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Правильный шестиугольник как построить без циркуля

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.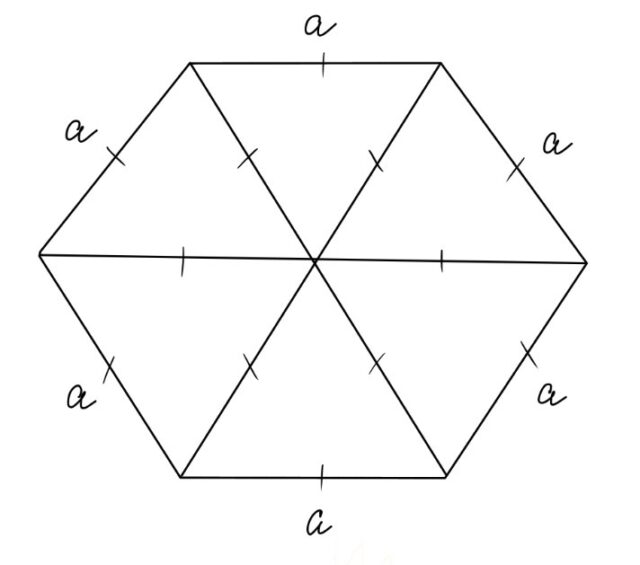

Вам понадобится

• Циркуль, линейка, карандаш, лист бумаги.

Инструкция

1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.

2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.

3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.

Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.

Вам понадобится

• Карандаш, лист бумаги, линейка

Инструкция

1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.

2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.

Видео по теме

Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.

Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.

Вам понадобится

• Карандаш, линейка, лист бумаги.

Инструкция

1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)

2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)

Видео по теме

Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.

Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.

Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.

Вам понадобится

• транспортир, угольник, циркуль, линейка

Инструкция

1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.

2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.

3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.

4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.

5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.

6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.

Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.

Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.

Вам понадобится

Инструкция

1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.

2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.

3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.

4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.

5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).

6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.

7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).

Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.

При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.

Инструкция

1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.

2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.

3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.

4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.

5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.

6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.

Видео по теме

Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.

Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…

Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…

Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…

Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…

Построение правильных многоугольников — Техническое черчение

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Как построить равносторонний шестиугольник — Морской флот

/

/

Как построить равносторонний шестиугольник

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.

Вам понадобится

• Циркуль, линейка, карандаш, лист бумаги.

Инструкция

1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.

2. Пос

Гексагональный иерархический пространственный индекс Uber

имеют решающее значение для анализа больших наборов пространственных данных, разделяя области Земли на идентифицируемые ячейки сетки.

Помня об этом, Uber разработал h4, нашу сеточную систему для эффективной оптимизации ценообразования и диспетчеризации поездок, а также для визуализации и изучения пространственных данных. h4 позволяет нам анализировать географическую информацию, чтобы устанавливать динамические цены и принимать другие решения на уровне города. Мы используем h4 как сетку для анализа и оптимизации на наших торговых площадках.h4 был разработан для этой цели и заставил нас сделать выбор, например, использовать шестиугольные иерархические индексы.

Ранее в этом году мы открыли исходный код h4 на Github, предоставив другим доступ к этому мощному решению, а на прошлой неделе мы открыли исходный код наших привязок JavaScript для h4. В этой статье мы обсудим, почему мы используем систему сеток, некоторые уникальные свойства h4 и как вы можете начать использовать h4.

Расчет с использованием сеток

Ежедневно на торговой площадке Uber происходят миллионы событий. Каждую минуту райдеры запрашивают поездки, водители-партнеры начинают поездки, а голодные пользователи запрашивают еду среди других действий на платформе. Каждое событие происходит в определенном месте, например, гонщик запрашивает поездку из дома, а водитель принимает этот запрос в своей машине всего в нескольких километрах от него.

Эти события позволяют Uber лучше понимать и оптимизировать рынок для пользователей наших сервисов.Например, эти события могут сообщить нам, что в определенной части города спрос больше, чем предложение, и скорректировать цены в ответ, или сообщить платформе, что есть два запроса на поездку в непосредственной близости от конкретного водителя на uberPOOL.

Для получения информации и анализа данных на рынке Uber требуется анализ данных по всему городу. Поскольку города географически разнообразны, этот анализ необходимо проводить с высокой степенью детализации. Анализ с высочайшей степенью детализации, точного места, где происходит событие, очень сложен и дорог.Анализ по областям, таким как кварталы в городе, намного практичнее.

Рис. 2. На картах выше показан процесс выделения точек с h4: автомобили в городе; автомобили в шестиугольниках; и шестиугольники заштрихованы числами автомобилей.

Мы используем систему сеток для группирования событий в шестиугольные области, другими словами, ячейки. Точки данных сгруппированы в шестиугольники и могут быть записаны с использованием данных с шестигранными разделениями. Например, мы рассчитываем всплеск цен, измеряя спрос и предложение в шестиугольниках в каждом городе, который мы обслуживаем.Эти шестиугольники составляют основу нашего анализа рынка Uber.

Шестиугольники были важным выбором, потому что люди в городе часто находятся в движении, а шестиугольники минимизируют ошибку квантования, возникающую при перемещении пользователей по городу. Шестиугольники также позволяют легко аппроксимировать радиусы, как в этом примере с помощью Elasticsearch.

Рисунок 3. Карта почтовых индексов Нью-Йорка (Манхэттен).

Есть и другие варианты, которые мы могли бы использовать для распределения событий по областям, например, многоугольные зоны вокруг областей.Это могут быть области почтового индекса, но такие области имеют необычные формы и размеры, которые бесполезны для анализа и могут быть изменены по причинам, совершенно не связанным с тем, для чего мы будем их использовать. Зоны также могут быть нанесены операционными группами Uber на основе их знаний о городе, но такие зоны требуют частого обновления, поскольку города меняются, и часто произвольно определяют границы областей.

Рис. 4. Случайно сгенерированные гексагональные кластеры покрывают город Сан-Франциско.

Сетевые системы могут иметь сопоставимые формы и размеры в городах, в которых работает Uber, и не подлежат произвольным изменениям.Хотя сеточные системы не выравниваются по улицам и районам в городах, их можно использовать для эффективного представления кварталов путем кластеризации ячеек сетки. Кластеризация может быть выполнена с использованием целевых функций, создавая формы, гораздо более полезные для анализа. Определение членства в кластере так же эффективно, как и операция поиска набора.

ч4

Мы решили создать h4, чтобы объединить преимущества гексагональной глобальной сеточной системы с иерархической системой индексации.

Глобальная сеточная система обычно требует как минимум двух вещей: проекции карты и сетки, накладываемой поверх карты.Картографическая проекция необходима для перехода от трехмерного места на Земле к двумерной точке на карте. Затем на карту накладывается сетка, образуя глобальную сеточную систему.

Этот процесс может быть выполнен бесчисленными способами путем комбинирования различных картографических проекций и сеток, например широко известной проекции Меркатора и квадратной сетки. Хотя этот простой метод сработает, у него есть ряд недостатков. Начнем с того, что проекция Меркатора имеет значительное искажение размера, поэтому некоторые ячейки будут иметь совершенно разные площади.Квадратные сетки также имеют недостатки, требующие нескольких наборов коэффициентов при использовании для анализа. Этот недостаток является результатом того, что квадраты имеют два разных типа соседей: один тип, с которым они имеют общее ребро (в четырех основных направлениях), и другой тип, с которым они имеют общую вершину (в четырех диагональных направлениях).

Рис. 5. Мы решили использовать гномонические проекции с центром на гранях икосаэдра (слева) для проекции карты h4, проецируя Землю как сферический икосаэдр (справа).

Для проекции карты мы решили использовать гномонические проекции с центром на гранях икосаэдра. Он проецируется от Земли в виде сферы к икосаэдру, двадцатигранному платоническому телу. Проекция карты на основе икосаэдра дает двадцать отдельных двухмерных плоскостей, а не одну плоскость. Икосаэдр можно развернуть разными способами, каждый раз создавая двумерную карту. h4, однако, не разворачивает икосаэдр для построения своей системы сеток, а вместо этого кладет свою сетку на сами грани икосаэдра, образуя геодезическую дискретную глобальную систему сеток.

Рисунок 6. Расстояния от треугольника до его соседей (слева), от квадрата до его соседей (в центре) и от шестиугольника до его соседей (справа).

Использование шестиугольника в качестве формы ячейки имеет решающее значение для h4. Как показано на рисунке 6, шестиугольники имеют только одно расстояние между центром шестиугольника и его соседями, по сравнению с двумя расстояниями для квадратов или тремя расстояниями для треугольников. Это свойство значительно упрощает выполнение анализа и сглаживания градиентов.

Рис. 7. h4 используется для создания сетки на одной грани икосаэдра.

Сетка h4 построена путем размещения 122 базовых ячеек над Землей, по десять ячеек на грань. Некоторые ячейки содержат более одного лица. Поскольку невозможно замостить икосаэдр только шестиугольниками, мы решили ввести двенадцать пятиугольников, по одному в каждой вершине икосаэдра. Эти вершины были расположены с использованием сферической ориентации икосаэдра Р. Бакминстера Фуллера, при которой все вершины помещаются в воду.Это помогает избежать всплытия пятиугольников в нашей работе.

Рис. 8. h4 позволяет пользователю разделить области на все меньшие и меньшие шестиугольники.

h4 поддерживает шестнадцать разрешений. Каждое более высокое разрешение имеет ячейки с одной седьмой областью более грубого разрешения. Шестиугольники нельзя полностью разделить на семь шестиугольников, поэтому более мелкие ячейки лишь приблизительно содержатся в родительской ячейке.

Идентификаторы для этих дочерних ячеек можно легко усечь, чтобы найти их предковую ячейку с более грубым разрешением, что обеспечивает эффективное индексирование.Поскольку дочерние ячейки содержатся только приблизительно, процесс усечения приводит к фиксированному искажению формы. Это искажение присутствует только при выполнении усечения идентификатора ячейки; при индексировании местоположений с определенным разрешением границы ячеек являются точными.

Начало работы с h4

Система индексирования h4 имеет открытый исходный код и доступна на GitHub. Сама библиотека h4 написана на C, и привязки доступны для ряда языков.Использование привязок — это рекомендуемый способ начать использовать h4. Uber опубликовал привязки для Java и JavaScript, а сообщество внесло привязки для других языков. Скоро появятся привязки для Python и Go.

Рис. 9. Точка (синяя, слева) и содержащий ее шестиугольник, центроид (светло-синий, середина) содержащего шестиугольника, а также точка и центроид содержащего шестиугольника (справа) изображают возможную разницу. между двумя.

Код: https: // github.com / uber / h4 / blob / master / examples / index.c

Основные функции библиотеки h4 предназначены для индексации местоположений, которая преобразует пары широты и долготы в 64-битный индекс h4, идентифицируя ячейку сетки. Функция geoToh4 принимает широту, долготу и разрешение (от 0 до 15, где 0 — самый грубый, а 15 — самый точный) и возвращает индекс. h4ToGeo и h4ToGeoBoundary являются инверсией этой функции, обеспечивая координаты центра и контур ячейки сетки, заданной индексом h4, соответственно.

После того, как вы проиндексировали данные с помощью h4, в h4 API появятся функции для работы с индексами.

Рисунок 10. Шестиугольники, соседствующие с индексом, с расстоянием 0 (слева; только исходный индекс), 1 (посередине; с соседями исходного индекса) и 2 (справа; с соседями соседей).

Код: https://github.com/uber/h4/blob/master/examples/neighbors.c

Соседние шестиугольники обладают полезным свойством аппроксимации окружностей с использованием системы сеток.Функция kRing предоставляет ячейки сетки в пределах расстояния k сетки от исходного индекса.

Рис. 11. Плотные шестиугольники, представляющие Калифорнию, резко контрастируют с компактными шестиугольниками, представляющими штат, требуя гораздо меньшего количества шестиугольников для представления той же площади.

Код: https://github.com/uber/h4/blob/master/examples/compact.c

Иерархический характер h4 позволяет эффективно сокращать точность (или разрешение) индекса и восстанавливать исходные индексы. Выше показаны некомпактные и компактные представления набора шестиугольников. В некомпактном представлении имеется 10 633 шестиугольника с разрешением 6, а в компактном представлении — 901 шестиугольник с разрешением до 6. В обоих случаях шестигранный индекс является 64-битным целым числом.

Точность одного индекса также может быть эффективно усечена с помощью побитовой операции или расширена до набора индексов более высокой точности.

Рисунок 12. h4 может представлять движение из одной ячейки в другую, здесь изображено стрелкой от исходной ячейки к целевой.

Код: https://github.com/uber/h4/blob/master/examples/edge.c

h4 имеет функции для направленных краев ячеек сетки, которые могут представлять движение от одной ячейки к другой. Направленные ребра могут быть сохранены как 64-битные целые числа и могут быть получены из двух соседних ячеек или путем нахождения всех ребер ячейки. При необходимости ребро можно преобразовать обратно в исходный или целевой индексы.

Движение вперед

h4 используется в Uber для количественного анализа нашего рынка, и теперь, когда его исходный код открыт, вы тоже можете гексагонизировать мир! Мы с нетерпением ждем, когда вы присоединитесь к сообществу h4, подписавшись на наш репозиторий на Github и написав твит с хэштегом # uberh4.

Карты, созданные с помощью MapboxGL.

Узнайте больше о наших поставщиках картографических данных.

Основными участниками библиотеки h4 являются Кевин Сар (Университет Южного Орегона), Джозеф Гилли (Uber), Ник Рабиновиц (Uber) и Дэвид Эллис (CarDash).

Подпишитесь на нашу рассылку новостей , чтобы быть в курсе последних инноваций от Uber Engineering.

Примеры черепах

Впервые опубликовано: 15 февраля 2014 г.

Последнее обновление: 11 апреля 2016 г.

---

Введение

Мое первое знакомство с программированием было в средней школе в течение первой недели занятий. Мой учитель объяснил, что мы будем изучать язык программирования под названием «Логотип», который позволит вам управлять воображаемой «черепахой» с ручкой, прикрепленной к ее хвосту, для рисования изображений и пакетов.

Затем нам дали толстый пакет примеров и дали возможность экспериментировать и делать все, что нам нравится, при условии, что мы выполняем определенное количество упражнений каждый день.

Я не уверен, сколько я фактически изучил, так как в основном я копировал и настраивал код вслепую, но я помню, что до сих пор очень весело играл с Logo.

Естественно, я был очень рад обнаружить, что Python, один из моих любимых языков программирования, имеет встроенный модуль с именем «turtle», очень похожий на Logo.Этот документ — попытка частично отразить дух исходного пакета примеров, который впервые познакомил меня с программированием.

Примечание. Я начал работу над этим документом около года назад, но на самом деле так и не успел завершить или обновить его, кроме нескольких примеров. В течение следующих нескольких месяцев я буду время от времени добавлять новые примеры, когда у меня будет время.

---

Пример 1. Построение линии

Одна из самых простых вещей, которые вы можете сделать с помощью модуля черепахи, — это нарисовать линию.Всегда есть четыре шага, которые вам нужно сделать, чтобы использовать модуль черепахи:

1. Импортировать модуль черепахи. Если мы пропустим этот шаг, не будет черепахи, которую нужно будет контролировать.
2. Создайте черепаху для управления.
3. Нарисуйте штуки. Делай что-нибудь. Это также автоматически создаст экран.
4. Выполнить turtle.done () . ( НЕ bob.done () !)

Обратите внимание, что turtle.done () приостанавливает выполнение программы.Вам нужно будет закрыть окно, чтобы продолжить.

Код

  # Шаг 1: Сделайте все команды "черепахи" доступными для нас.
импортная черепаха

# Шаг 2: Создайте новую черепаху. Мы назовем это "боб"
bob = черепаха. Черепаха ()

# Шаг 3. Двигайтесь в направлении Боба на 50 пикселей.
боб. вперед (50)

# Шаг 4: Готово!
turtle.done ()  

Ожидаемый результат

---

Пример 2: Рисование квадрата.

Строки скучные. Мы можем вращать черепаху, чтобы рисовать более интересные фигуры.

Код

  импортная черепаха

глупый = черепаха. черепаха ()

глупый. вперед (50)
silly.right (90) # Повернуть по часовой стрелке на 90 градусов

глупый. вперед (50)
глупый. правильный (90)

глупый. вперед (50)
глупый. правильный (90)

глупый. вперед (50)
глупый. правильный (90)

turtle.done ()  

Ожидаемый результат

Дополнительные примечания

Две команды черепахи, которые мы изучили до сих пор: forward (x) , которые перемещают черепаху вперед в направлении, в котором она смотрит, на x количество пикселей, и справа (d) , что делает его поворот по часовой стрелке на d количество градусов.

Две дополнительные ключевые команды: назад (x) , что заставляет черепаху двигаться назад, и

Введение в гексагональную геометрию

Содержание

Введение

Ниже приводится краткий обзор некоторых элементарных свойств шестиугольников, и почему они могут быть полезны. Он не претендует на всестороннее рассмотрение данного предмета. Меня особенно интересуют математические свойства шестиугольников и, в некоторой степени, их роль в мире природы.Я избегал обсуждения шестиугольников, поскольку они имеют отношение к человеческой культуре, религии, истории и другим «местным» проблемам, хотя в этих областях есть много интересных примеров шестиугольников и шестиугольников, и они, несомненно, будут более подробно рассмотрены в другом месте в другое время. .

Эта статья находится в стадии разработки и на самом деле не «закончена» в каком-либо значимом смысле. Он актуален на момент последнего обновления. Я намерен в какой-то момент заменить или, по крайней мере, дополнить его более полным и красноречивым обзором гексагональных концепций.Имейте в виду, что в этой статье исследуется лишь очень небольшая часть интересных свойств шестиугольников, и есть надежда, что более полное представление об их качествах появится благодаря сумме разнообразного материала, доступного на этом сайте.

Примечание о терминологии: По моему обыкновению, если не указано иное, «шестиугольник» относится только к правильным шестиугольникам. Кроме того, я склонен довольно свободно говорить о «шестиугольных» то и то. Описывая вещи как «шестиугольники», я часто имею в виду в очень широком смысле все шестиугольные и шестиугольные симметрии, и не обязательно правильные шестиугольники как таковые.

Некоторые наблюдения о шестиугольниках

Шестиугольник — это замкнутая плоская фигура с шестью ребрами и шестью вершинами. Правильный шестиугольник — это выпуклая фигура со сторонами одинаковой длины и внутренними углами 120 градусов. Он имеет шесть симметрий вращения и шесть симметрий отражения, составляющих группу диэдра D ₆ .

Свойства шестиугольников многочисленны и интересны. На первый взгляд выделяются несколько фактов о них:

• Шестиугольники — это один из трех правильных многоугольников, которые составляют мозаику евклидовой плоскости (наряду с квадратами и треугольниками).
• Гексагональная мозаика комбинаторно идентична плотной упаковке кругов на плоскости.
• Шестиугольники — единственный правильный многоугольник, который можно подразделить на другой правильный многоугольник. (Насколько мне известно, шестиугольники — единственный правильный многогранник любой размерности, обладающий этим свойством.)
• В связи с этим шестиугольники — это уникальный правильный многоугольник, такой, что расстояние между центром и каждой вершиной равно длине каждой стороны (разделяя это свойство с кубооктаэдром в 3-м пространстве).
• Шестиугольники — это первые многоугольники, возрастающие по количеству сторон, которые не образуют грани правильного выпуклого многогранника в евклидовом пространстве. Три многоугольника с меньшим количеством сторон составляют поверхности пяти платоновых тел, но для этой цели нельзя использовать многоугольник с шестью или более сторонами. Следствием этого является то, что ни один правильный многогранник ни в каком измерении не имеет шестиугольных граней, хотя многие из них имеют шестиугольные или шестиугольно-симметричные вершины или другие элементы.
• Шестиугольники — это пермутоэдры третьего порядка, что означает, что каждая вершина шестиугольника может быть описана декартовыми координатами с использованием одной из шести перестановок чисел 1, 2 и 3.Такой шестиугольник лежал бы на плоскости, состоящей из всех точек с координатами, которые в сумме дают 6, и делил бы пополам куб единичной длины 2 между координатами 1 и 3.

Еще одна интересная особенность шестиугольников — и, пожалуй, наиболее поразительный факт о них — это то, что они действительно имеют шесть сторон. Позвольте нам тогда перечислить некоторые интересные факты о числе шесть:

• Шесть — составное число, второе по величине составное число и первое совершенное число.То есть 1 * 2 * 3 = 1 + 2 + 3 = 6.
• С другой стороны, шесть — это единственное число, которое является суммой и произведением трех последовательных натуральных чисел (1, 2 и 3).
• Шесть — наименьшее составное целое число без квадратов и, в более широком смысле, первое натуральное число с двумя различными простыми множителями (2 и 3).
• Кубики имеют шесть сторон, и они тоже довольно полезны.

И так далее. Очевидно, что большинство уникальных и интересных свойств шестерки в конечном итоге проистекает из того факта, что это произведение и сумма первых трех натуральных чисел, и что в более философском смысле его можно рассматривать как объединение архетипические ценности единства, двойственности и троичности в несколько уравновешенное целое.Единство разделяется на двойственность, которая примиряется в троице (один плюс два или два, объединяющихся в одно), которая затем рекомбинируется с двойственностью и единством — либо аддитивно, либо мультипликативно — чтобы произвести наши уважаемые шесть.

Конечно, есть много других гексагональных и гексагональных чисел, и было бы ошибкой ассоциировать гексагональность только с шестью. Семерка, например, часто занимала видное место в человеческой культуре и, в частности, в некоторых религиозных традициях.Если вернуться назад и посмотреть на различные геометрические формы, связанные с такими семерками, часто становится очевидным, что они сконструированы так, чтобы образовывать шесть периферийных объектов вокруг одного центрального объекта — в виде шестиугольных окружностей или шестиугольной мозаики. На первый взгляд негексагональные числа, такие как восемь и десять, также имеют гексагональный оттенок, как и различные центрированные шестиугольные числа, правильные шестиугольные числа и так далее. Не говоря уже о числах, кратных шести, например, двенадцати, что также является действительно большим числом само по себе (добавление делимости на 4 в ситуации 1, 2, 3).Но, конечно, само собой разумеется, что шесть имеет отчетливую связь с гексагональностью, и в этом отношении стоит знать ее уникальные и интересные свойства.

В конечном итоге я считаю, что чем больше вы изучаете математические и физические основы Вселенной, тем более заметными и интересными становятся шестиугольники, шестерки и их различные аналоги в других математических системах. Постулирование какой-либо всеобъемлющей интерпретации этого выходит за рамки данной статьи, но это стоит отметить и учесть в наших интерпретациях реальности и во взаимоотношениях с ней.

Здесь я хотел бы остановиться на нескольких шестиугольных вопросах, поднятых выше.

Основная геометрия шестиугольников

Давайте сначала рассмотрим более внимательно основные пропорции и соотношения благородного шестиугольника:

Апофема правильного шестиугольника равна половине квадратного корня из 3. Это можно продемонстрировать с помощью единичного шестиугольника, где каждой стороне дана длина 1. Затем мы можем нарисовать прямоугольный треугольник, используя диаметр от вершины к вершине. шестиугольника как гипотенузы.Поскольку известно, что диаметр такого шестиугольника равен 2, у нас остается одно неопределенное ребро нашего треугольника, равное расстоянию между двумя противоположными сторонами шестиугольника (что в два раза больше апофемы). Назовем это ребро x . Теорема Пифагора говорит нам, что 1 ² + x ² = 2 ² . Отсюда следует, что 1 + x ² = 4, x ² = 3, и, следовательно, x = √3. Следовательно, «высота» «ширина» правильного шестиугольника равна √3 / 2. Quod erat manifestrandum.

Интересным следствием этого является то, что правильные шестиугольники и равносторонние треугольники имеют точно такое же отношение «ширины» к «высоте». То есть минимальный диаметр шестиугольника и треугольника равен √3 / 2 его максимального диаметра. В самом деле, √3 является повторяющимся значением во всей треугольной и шестиугольной геометрии — например, диагональное расстояние между двумя противоположными вершинами куба также равно √3 (сравните с диагональной шириной квадрата, которая равна √2, по причинам, аналогичным указанные выше).Как следствие, √3, конечно же, занимает видное место в плоской тригонометрии, где она проявляется в выражении различных значений 60 и 30 градусов.

Площадь шестиугольника также может быть вычислена с помощью √3. Давайте сначала определим длину ребра нашего шестиугольника как s . Затем мы можем нарисовать прямоугольник между двумя противоположными краями шестиугольника с площадью s ² √3. Если мы затем посчитаем, что у нас осталось 4 правых треугольных сечения, и что сам шестиугольник можно считать состоящим из 12 таких треугольников, 8 из которых мы включили в наш прямоугольник, становится ясно, что общая площадь шестиугольника в полтора раза больше площади прямоугольника.Таким образом, s ² √3 (3/2). Quod erat faciendum.

(Это также пример более общего принципа, согласно которому площадь правильного выпуклого многоугольника равна произведению периметра и апофемы, деленных на 2 (в данном случае 6s√3 / 2/2). Это связано с к тому факту, что мы можем разделить правильный выпуклый многоугольник со сторонами n на 2 прямоугольных треугольника n , проведя отрезки линии от центра к каждой вершине, а также от центра к середине каждого ребра.Затем мы можем предположить, что каждые 2 сформированных таким образом прямоугольных треугольника можно объединить в прямоугольник с площадью апофемы, умноженной на половину длины ребра. Таким образом, просто разделив произведение апофемы на общий периметр пополам, мы приходим к общей площади многоугольника.)

Шестиугольная мозаика

Как отмечалось ранее, шестиугольники можно выложить плиткой или мозаикой в ​​виде регулярного рисунка на плоской двумерной плоскости. То есть шестиугольник может быть ограничен шестью другими шестиугольниками, которые сами могут быть ограничены шестью шестиугольниками (включая друг друга) и так далее, бесконечно в любом направлении, без пустого пространства.Обратите внимание, что хотя существует любое количество потенциальных мозаик, состоящих из двух или более типов многоугольников, только шестиугольники, квадраты и треугольники могут сами по себе образовывать такие правильные мозаики. (Аналогично, в трех измерениях, среди однородных многогранников, только шестигранный куб и шестигранный аналог усеченного октаэдра могут сами по себе образовывать заполняющие пространство мозаики.)

Следовательно, шестиугольник — это, конечно, правильный многоугольник с высшей стороной в виде мозаики. Это делает его уникально важным во множестве областей, так как он имеет преимущество в том, что каждый составляющий шестиугольник более или менее равномерно отделен от его соседей.То есть любая заданная точка внутри шестиугольника (будь то мозаика из шестиугольников или нет) ближе к центру этого шестиугольника, чем любая заданная точка в квадрате или треугольнике равной площади. Поскольку квадраты и треугольники имеют более острые углы, точки около их углов находятся дальше от точек в другом месте их области, чем они были бы в аналогичных местах шестиугольника. То же самое будет верно и для любого многоугольника с более высокой стороной — идеальная эффективность для ограждения данной области, в конечном счете, является кругом.Но опять же, у шестиугольников есть преимущество тесселяции. Таким образом, для любой задачи, требующей как регулярной сетки ячеек, так и элементов, и эффективного ограждения области этой ячейки, гексагональная тесселяция является логичным и необходимым выбором. Общие примеры такого использования гексагональных ячеек можно найти в таких разнообразных областях, как клеточные автоматы, статистическая выборка, настольные игры, компьютерные игры, соты уважаемой пчелы и т. Д.

Связанное с этим свойство гексагональной мозаики состоит в том, что она не создает диагональных краев.(Под «диагональю» здесь я подразумеваю соседей, которые имеют общую границу только вершины, а не границу ребра — я не знаю более точного математического термина для этого, хотя я знаю, что это не совсем то, что «диагональ» означает в самом строгом смысл этого термина.) Если вы посмотрите на мозаики из треугольников и квадратов, вы, конечно, увидите, что оба имеют диагональные связи между соседними элементами в их вершинах. В квадратной тесселяции каждый квадрат соединяется с одним квадратом непосредственно с каждой стороны и одним квадратом по диагонали в каждой вершине, всего восемь соседних квадратов, а в треугольной тесселяции каждый треугольник соединяется с одним треугольником с каждой стороны и с тремя треугольниками по диагонали на каждой. вершина, всего двенадцать соседних треугольников.Эти диагональные соединения, конечно, являются ключом к способности квадратов и треугольников образовывать правильные многогранники — удалив диагональных соседей вокруг квадрата, можно легко загнуть оставшиеся соседние квадраты, пока они не соединятся друг с другом напрямую, чтобы сформировать куб, и аналогичным образом удаляя одного, двух или трех диагональных соседей из треугольника, можно сложить оставшиеся треугольники в икосаэдр, октаэдр или тетраэдр соответственно. (Хотя следует отметить, что, хотя оба диагонально-мозаичных правильных многоугольника образуют правильные многогранники при таком складывании, на поверхности нет особой причины, по которой это должно быть .) Наоборот, поэтому шестиугольники не могут образовывать собственные правильные многогранники. Каждый внешний угол шестиугольника равен 120 градусам, а единственная возможная конфигурация вершины — в евклидовом пространстве — с тремя соседними углами в сумме 360 градусов (за исключением, конечно, «вырожденного» шестиугольного диэдра, который не особенно полезен для наши цели здесь).

Гексагональная тесселяция — двойная треугольная тесселяция — вы можете превратить первое во второе, заменив все вершины треугольниками, а все шестиугольники вершинами.Точно так же в треугольной тесселяции, если вы замените все треугольники вершинами, а все вершины шестиугольниками, у вас снова останется шестиугольная мозаика. (Любой многогранник или мозаика с обратными количествами внешних элементов может быть перевернут по тому же принципу: октаэдр является обратным кубу, а икосаэдр — обратным додекаэдру — каждый представляет собой переворачивание вершины / грани своего аналога. Это могут быть представлены в виде записи путем изменения символа Шлефли конкретного объекта — в случае гексагональной и треугольной мозаики, путем изменения {6,3} на {3,6}, или наоборот.) Кроме того, поскольку шестиугольники можно разделить на равносторонние треугольники, а равносторонние треугольники можно объединить в шестиугольники, мозаику треугольников можно рассматривать как простое подразделение шестиугольника или наоборот.

Последнее преимущество гексагональной мозаики или гексагональной решетки, заслуживающее внимания, — это ее прочность на сжатие и растяжение и эффективность по сравнению с другими вариантами мозаики. Если мы рассмотрим абстрактную физическую «структуру», образованную отрезками прямых между вершинами правильной многоугольной мозаики (т. Е.е. проволочная сетка), ясно, что такая структура, сформированная в виде шестиугольной решетки, обеспечит идеальное сочетание эффективности и прочности по сравнению с аналогичными треугольными или квадратными структурами. Либо треугольная, либо шестиугольная структура, построенная таким образом, будет явно сильнее, чем квадратная структура, и хотя треугольная структура, при прочих равных условиях, будет прочнее шестиугольной, она также будет использовать больше материала (с шестью линиями, соединяющимися через каждая вершина вместо трех) и, таким образом, будет менее «эффективным» — хотя для конкретных приложений, очевидно, это может быть предпочтительнее.

Тот факт, что квадратные решетки не имеют той же прочности, что и шестиугольные или треугольные решетки, становится очевидным, когда кто-то изучает иллюстрацию трех структур, представляя, что в каждой вершине линейные сегменты структуры сдвигаются или разрываются с той силой, с которой они будут действовать. физическая структура. Ясно, что с четырьмя сегментами, выходящими на точные углы 90 градусов в каждой вершине, квадратная структура легко срезается либо по горизонтали, либо по вертикали — у нее нет других углов, поддерживающих ее структуру, поэтому они просто как бы шатаются.И наоборот, в треугольной и шестиугольной конфигурации линейные сегменты, сходящиеся под углами 60 и 120 градусов, предотвращают любое срезание или сжатие — они уравновешивают друг друга и равномерно распределяют нагрузку (какой бы она ни была).

Например, если вы вообразите шестиугольную или треугольную решетку, «удерживающую» объект, ясно, что чередующиеся углы шестиугольной и треугольной решеток будут делать больше для распределения веса на нижние уровни, чем квадратная решетка с ортогональными ограничениями.Тот же принцип легко применим и к приложениям распределения силы в трех измерениях — таких, как мы видим, например, в замечательной прочности углеродных нанотрубок на разрыв, в распределении веса по геодезическим куполам и так далее.

Шестиугольники и окружности

Гексагональная упаковка — наиболее эффективная система для упаковки кругов на плоской плоскости. То есть, как и в случае с шестиугольной мозаикой, вы можете разместить шесть соседних кругов одинакового размера вокруг круга и шесть кругов вокруг каждого из них, и так до бесконечности, так что расположение кругов идентично расположению шестиугольников в гексагональная мозаика.Другими словами, можно вписать круги в каждый шестиугольник в шестиугольной мозаике, удалить шестиугольники, и в результате получатся идеально плотно упакованные круги. Это полезно и интересно по ряду причин, например, потому, что позволяет легко моделировать гексагонально упакованные круги с помощью шестиугольников или треугольников, когда это необходимо.

Интересное явление, связанное с этим пересечением круговой и гексагональной геометрии, заключается в том, что гексагональные узоры часто появляются спонтанно, когда силы природы пытаются приблизиться к окружностям.(Это, без сомнения, большая часть причины, по которой шестиугольники обычно считаются очень «естественной» формой.) Например, конвективные ячейки часто образуют шестиугольники. Поскольку каждая ячейка естественно стремится к наиболее эффективному замкнутому пространству, они имеют тенденцию к округлости, но поскольку каждая ячейка имеет любое количество соседних ячеек, прижимающихся к ней, результатом является своего рода квазигексагональная мозаика. Подходящим примером этого может быть Дорога гигантов в оккупированной Ирландии: когда базальтовая лава, которая сформировала структуру, первоначально остывала, она сжималась в примерно цилиндрические ячейки.Когда клетки охлаждались в твердую породу, они, естественно, приобретали шестиугольную геометрию упакованных кругов.

Также стоит отметить, что шестиугольники играют важную роль в трехмерных сферах плотной упаковки, как в гексагональной плотной упаковке, так и в гранецентрированных кубических системах. И HCP, и FCC состоят из «листов» гексагонально упакованных сфер — они различаются только тем, как листы складываются вместе. Следует отметить, что, несмотря на их соответствующие названия, можно утверждать, что гранецентрированная кубическая упаковка на самом деле более «гексагональна», чем так называемая гексагональная упаковка — последняя получила свое название скорее из-за отсутствия кубичности, чем из-за преобладание гексагональности.Обратите внимание, что и HCP, и FCC значительно менее эффективны, чем гексагональная упаковка в двух измерениях: первая имеет плотность π / (3√2), а вторая — π / √12. Очевидно, что также известны регулярные плотные упаковки n-сфер до 8 измерений, которые могут включать или не включать гексагональные или гипергексагональные топологии.

Шестиугольники и треугольники

Во многих отношениях отношения между треугольниками и шестиугольниками являются продолжением отношений между шестиугольниками и кругами.Я считаю их частью одного неразрывного геометрического континуума (основанного, как я полагаю, на довольно очевидном факте, что самое близкое расположение трех кругов одинакового размера находится в вершинах равностороннего треугольника с длиной ребра, равной диаметру кругов) . Но пока давайте посмотрим конкретно на отношения между треугольниками и шестиугольниками:

Как уже отмечалось, правильный шестиугольник можно разделить на шесть равносторонних треугольников. Шестиугольник и треугольник — единственные два правильных многоугольника, и я считаю, что только два правильных многогранника обладают этим свойством.В дополнение к тому, что шестиугольник делится на равносторонние треугольники, треугольник, конечно, сам делится на подтреугольники, и поскольку группировка любых шести треугольников, расположенных вокруг вершины, дает шестиугольник, треугольники также могут делиться на шестиугольники, хотя с оставленными треугольными промежутками над. Треугольник, разделенный на 9 подтреугольников, можно представить как шестиугольник с тремя равносторонними треугольниками, образованными продолжением ребер чередующихся сторон шестиугольника до их встречи (например, на рисунке Тетрактиса).

Топологически родственная концепция — это понятие треугольных чисел, которые можно визуализировать как гексагонально упакованные круги, шестиугольники или точки внутри треугольника. В частности, треугольные числа можно определить как сумму всех натуральных чисел от 1 до n , где n — количество единиц на каждой стороне рассматриваемого фигурного треугольника. То есть предположим, что вы взяли три точки и расположили их в виде треугольника. На каждой стороне треугольника две точки, и 1 + 2 = 3.Добавьте еще три точки к основанию этого треугольника, и у вас будет еще один треугольник, в данном случае с тремя точками на каждую сторону, и 1 + 2 + 3 = 6 (что также является произведением 1, 2 и 3, как упоминалось ранее). И так далее. Треугольное число с длиной стороны n также можно рассчитать как n * ( n +1) / 2 — таким образом, 3 * (3 + 1) / 2 = 3 + 2 + 1 = 6.

Та же фигуральная шестиугольная решетка также используется для центрированных шестиугольных чисел или шестнадцатеричных чисел, которые аналогичны треугольным числам, но, конечно, с шестиугольниками вместо треугольников.(По причинам, которые мне трудно понять, термин «шестиугольное число» зарезервирован для фигуры шестиугольного контура, которая на самом деле не очень похожа на то, что подразумевается под «треугольным числом» или «квадратным числом», по крайней мере, в некотором смысле что я считаю особенно интересным.) Шестнадцатеричное число n ^th может быть выражено как шестикратное треугольное число ( n — 1) плюс один или как n * (n-1) * 3 + 1, который можно понимать как сумму трех прямоугольников плюс центральная точка.

Еще один интересный факт о шестнадцатеричных числах заключается в том, что сумма первых n шестнадцатеричных чисел равна кубу n . Например, 1 + 7 = 2 ³ = 8, 1 + 7 + 19 = 3 ³ = 27, 1 + 7 + 19 + 37 = 4 ³ = 64 и так далее. Чтобы понять это, представьте, что вы смотрите на угол куба таким образом, что куб выглядит как шестиугольник. Представьте, что куб на самом деле состоит из подкубиков, расположенных в виде числа в кубе. Первый кубик в углу можно рассматривать как первое шестнадцатеричное число, равное 1.Ниже и вокруг него расположены семь других кубиков, образующих слой кубиков вокруг углового куба, который можно рассматривать как второе шестнадцатеричное число, которое на самом деле равно 7, и так далее. Шестнадцатеричные числа можно представить себе как последовательные «оболочки» кубиков, исходящие из углового куба. Таким образом, кубы и шестнадцатеричные числа — это просто разные образные способы описания одних и тех же значений — куб n может быть расположен либо как куб, либо как пирамида из шестиугольников с базовой длиной n , и разница между любыми два последовательных куба — это шестиугольник.Мы снова видим взаимосвязь между шестигранным шестиугольником и шестигранным кубом — и, в более широком смысле, между шестиугольником и шестью «сторонами» самого трехмерного пространства.

Заключение

Опять же, эта статья лишь поверхностно коснулась многих интересных свойств шестиугольников и их аналогов. В самом деле, шестиугольники появляются в очень необычных местах в более абстрактных математических системах, и я в целом подозреваю, что если бы вы наметили все логические взаимосвязи математики, как их понимает и определило человечество, шестиугольник будет занимать видное место как повторяющаяся тема во всей структуре.

По мере развития человеческого общества мы, несомненно, будем находить все больше и больше приложений для универсального и эффективного шестиугольника. Будь то мозаика наших настольных игр, формирование наших эффективно замкнутых структур или помощь нам в лучшем понимании фундаментальных математических концепций, с течением времени мы обязательно обнаружим, что живем во все более и более шестиугольном мире. Является ли совпадением то, что научно-фантастические фильмы и телешоу — особенно те, которые происходят в открытом космосе — часто показывают шестиугольные двери, шестиугольные космические корабли, шестиугольную архитектуру и так далее? Думаю, нет.Провидцы и художники нашего общества уже видели, что грядет, и что станет очевидным для наших потомков: мы живем в шестиугольном мире, упорядоченном по шестиугольным принципам. Шестиугольники не могут быть решением всех мировых проблем. Они могут даже не быть решением очень многих проблем. Но они будут решением некоторых проблем, а это больше, чем вы можете сказать о многих вещах.

Круговые шестиугольные тайловые карты на сфере

В некоторых играх есть тайловые карты, которые повторяются.Цивилизация, например, позволяет вам уходить с левой стороны карты и перемещаться к правой стороне. Вы не можете уходить за пределы верхней или нижней части карты. В трехмерном пространстве это будет цилиндр . В некоторых играх также можно переходить от верхней стороны к низу, и наоборот. В трехмерном пространстве это будет тор .

В большинстве игр с круговыми мозаичными картами не используется сфера , как на реальной планете. Каковы его свойства?

1. Вы можете идти на запад / восток и перемещаться по карте.Это похоже на цилиндр или тор.
2. Вы можете идти на север / юг, но вы делаете , а не , оборачиваясь на другую сторону. Это похоже на цилиндр, но не на тор.
3. Вы можете пройти мимо северного / южного полюсов и остаться на этом полюсе, но лицом к югу / северу, а не север / юг. Это не похоже на цилиндр или тор.
4. Переход на запад / восток для обхода карты занимает меньше времени (меньшее расстояние) около полюсов, чем около экватора. Это не похоже на цилиндр или тор.

Разве это не круто? Почему в играх с мозаичной картой это не используется?

• Вы не можете выложить сферу равномерные квадратные или шестиугольные плитки (так сказал Эйлер! ^[2] ). Если вы попытаетесь выложить плитку из шестиугольников (разделив икосаэдр), у вас останется двенадцать пятиугольников. На изображении справа их легко заметить, но даже на карте с миллионами плиток у вас все равно будут эти двенадцать пятиугольников, скрытых среди миллионов шестиугольников.
• Необходимость в более узких полярных регионах означает, что они имеют более сложную систему координат, которая не позволяет создавать карты с прямоугольной сеткой.
• Необходимость менять направление при прохождении вехи затрудняет ориентацию камеры. У вас не может быть камеры, которая всегда смотрит на север. Он должен либо свободно вращаться, либо переворачиваться, когда вы проходите мимо шеста.

Итак, может быть непрактичным, выровнять сферу на плоской сетке, , ​​но я все равно хотел исследовать это . (Примечание: / x / в URL-адресе — это то место, где я помещаю свои быстрые неотшлифованные проекты, подобные этому.)

Первая проблема: какую систему координат я должен использовать для представления позиции и направления игрока таким образом, чтобы ходьба вокруг полюса короче, чем обход экватора? Распространенный способ мозаики сферы — разделить икосаэдр.(Примечание: если вы хотите использовать квадратные плитки вместо шестиугольников, разверните куб.) Этот икосаэдр в развернутом виде может выглядеть так:

Вторая проблема: что мне делать с оставшимися пятиугольниками? Они не будут работать с плоской тайловой картой. Я попробую скрыть пятиугольники , просто не позволяя вам приближаться к ним. Это будет работать только в играх, где вы идете пешком / за рулем, но не в играх, где вы можете уменьшать масштаб или свободно управлять камерой.

Третья проблема: что должно произойти, когда вы пройдете полюс? Я собираюсь повернуть камеру и сделать так, чтобы она позволяла вам видеть только окрестности.

Идея 1: двухуровневая система координат

Рассматривайте каждую область отдельно. Следите за тем, в каком регионе вы находитесь, а затем сохраняйте локальные координаты x, y внутри этого треугольника. При переходе границы в другую область вычислите новые x, y.

Расстояния и векторы, пересекающие границу области, становятся жесткими. Для локальных расчетов нет искажений по расстоянию или углу. Поскольку пересечение региона является сложным, лучше избегать боевых действий или даже пересечения территорий с сушей.

Идея 2: предел выпуклой координаты

Используйте одну координату x, y для всего мира, но ограничьте ее этой формой. Если вы попытаетесь выйти за границу y, вы остановитесь на краю. Если вы попытаетесь превысить границу x, вы обернетесь. Однако треугольники искажены, особенно возле полюсов.

Хотя глобальные вычисления могут быть немного лучше, расстояния и углы искажаются локально. Не думаю, что это сработает.

Идея 3: телепортировать регионы

Используйте одну координату x, y для всего мира, но ограничьте ее формой синей области.Если вы попытаетесь выйти за границу y, вы остановитесь на краю. Если x уходит с левой / правой стороны области треугольника в красную область, вы телепортируетесь в ближайшую допустимую область зеленой области. Это не работает рядом с тройными точками (где находятся пятиугольники), но если вы все равно не можете приблизиться к пятиугольникам, это не должно быть проблемой. Нам нужно перевести как позиции, так и направления в новый треугольник.

Наведите указатель мыши на красные области телепорта

Это своего рода гибрид идеи 1 (отдельные регионы, двухуровневые координаты) и 2 (все одна область, одна координата).В десяти тропических регионах все взаимосвязано; пересечение области легко и действует как тор. В десяти умеренных / полярных регионах они разделены; пересечение региона требует изменения координат и направлений. Как и в случае с идеей 1, для локальных расчетов нет искажений расстояния или угла. Преимущество перед идеей 1 состоит в том, что у вас могут быть более крупные континенты, пересекающие любую границу, включающую один тропический регион. Преимущество перед идеей 2 в том, что отсутствуют локальные искажения.

Это то, над чем я работал: вы можете ездить (WASD или стрелки), и вы видите повсюду гексагональную сетку, но основное поведение — примерно сфера.Вам нужно держаться подальше от пятиугольников; зоны опасности — темно-серые шестиугольники. Это работает в Chrome, но не во всех браузерах. Сожалею.

Идея состоит в том, чтобы отрегулировать треугольные области около полюсов, чтобы они были смежными с теми, в которых находится игрок. Затем, когда игрок уходит, мы отрегулируем их назад, чтобы они не были видны. Область рядом с игроком всегда выглядит плоской , пока вы не приближаетесь к пятиугольникам.

Я сделал тайлы довольно большими для этой демонстрации, но в реальной игре у вас может быть карта гораздо большего размера с миллионами маленьких гексов, и вы никогда не подойдете слишком близко к пятиугольникам.Вы не можете разрешить проигрывателю уменьшать масштаб, чтобы эта функция работала, если только вы не хотите переключиться в режим 3D-сферы при уменьшении масштаба.

Реализация: определите регион, в котором находится игрок, затем нарисуйте этот регион плюс три соседних региона. Однако для этой демонстрации я применил немного более простой подход: определил «столбец» с четырьмя регионами, в котором находится игрок, и отрендерил эти четыре плюс шесть соседних регионов. Я еще не рассчитал математически, как далеко от пятиугольников нам нужно оставаться, но для демонстрации я просто настроил его, пока он не стал достаточно хорошим.

В моей быстрой и грязной демонстрации есть некоторые ошибки, а также некоторые особенности, которые я хотел добавить:

• Области около пятиугольников являются запрещенными зонами, но демонстрация позволяет вам ездить туда.
• Он не работает в разных браузерах (по причинам, которые я не понял).
• «Сфера» должна быть изображена в виде сферы, а не икосаэдра.
• Сфера должна включать числовые метки и позицию игрока.

Однако я активно не поддерживаю эту идею, поэтому я не собираюсь тратить на нее сейчас много времени.

Разделенные икосаэдры имеют обычную форму, потому что они больше всего похожи на сферы, но мы можем использовать любое из Платоновых тел или усеченных тел, чтобы построить карту сферической формы. ^[3] :

Solid	Число сторон	Форма сторон	Мозаика
Икосаэдр	20	треугольников	треугольник, шестиугольник
Додекаэдр 9023	12	пятиугольников
Октаэдр	8	треугольники	треугольник, шестиугольник
Куб	6	квадратов	квадрат
Тетраэдр	4	треугольников

треугольник квадрат

В частности, развернутый куб был бы первым, на что я бы посмотрел, если бы мне понадобились квадратные плитки:

Развернутый тетраэдр (1 ^[4] , 2 ^[5] ) сильно искажен относительно сферы, но в игра, которая может быть в порядке.Основным преимуществом является то, что мы можем использовать прямоугольную систему координат , если мы приклеим правую половину треугольника 3 к левой половине треугольника 0:

1. Обращение влево / вправо просто: установите x = x% 2 .
2. Обтекание сверху / снизу тоже относительно просто: установите x = 2-x и оставьте y в покое, и поверните камеру игрока так, чтобы она указывала на юг, а не на север, или наоборот. Переход от треугольника 1 вверх ведет к треугольнику 3 и наоборот; движение вниз из треугольника 0 приводит к треугольнику 2 и наоборот.

Подобно подходу тетраэдра, квинкуциальная проекция Пирса ^[6] и квадратная проекция Гюю ^[7] и квадратная проекция Адамса ^[8] также имеют простую циклические системы координат. См. Эту визуализацию Peirce ^[9] из @mbostock. Оба являются конформными проекциями ^[10] , сохраняющими углы и местный масштаб.

No related posts.