Схемы сложные: Сложные оригами | Оригами из бумаги
Самые сложное оригами из бумаги, схемы |
В последние несколько лет такой вид декоративно-прикладного искусства как оригами набрал большую популярность. Своими корнями эта техника уходит очень далеко в историю – в древний Китай, где и появилась бумага. Однако наибольшую популярность и фактическим родоначальником оригами является Япония. Именно от японского слова происходит и название самого искусства – «ори» переводится как «складной» или «сложенный» и «ками» – «бумага». Нужно отметить, что первоначально оригами в основном использовалось в религиозных обрядах стран дальнего востока, а также составляло плотную часть культуры этих стран, так как умение красиво складывать бумагу считалось признаком хорошего тона.
Сложное оригами дракон из бумаги видео мастер-класс
Оригами можно подразделить на простое и сложное.
Сложное оригами из бумаги подразделяется на два основных вида – оригами из одного листа и из нескольких, модульное оригами . Как правило второй вид оригами является более сложным, чем первый, но бывают исключения. Однако это не значит, что фигуры из нескольких листов оригами будут выглядеть, что называется, причудливее. Чаще всего несколько листов бумаги используют для придания лучшей детализации и визуальности бумаги.
Интересно, что для сложного оригами из бумаги даже было проведено специальное математическое исследование, которое было направлено на улучшение качества этого вида оригами и на увеличение количество возможных фигур.
Нужно отметить, что сегодня, используя сложное оригами из бумаги можно придать форму абсолютно всему – не только реальным объектам, но и воображаемым.
Один из модных современных трендов в оригами – складывание объектов, не имеющих формы, например, страха, любви или счастья. Можно при помощи сложного оригами придать конкретную форму своим чувствам и эмоциям (например, страх у кого-то ассоциируется с летучей мышью или пауком), а можно и абсолютно абстрактную (например, в виде какой-то фигуры), что будет смотреться весьма свежо и необычно.
Чем более глубже и детальнее изучить оригами и чем большую популярность оно обретает, тем больше популяризируется именно сложное оригами из бумаги, которое дает больший простор для абстрактных фантазий.
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
|
5 (2506 votes)
6 (2633 голосов)
7 (1078 votes)
Тишин
5 (115 votes)Схемы оригами (от простого к сложному)
В этом разделе мы поговорим о том, как научиться складывать оригами по схемам расположенным по сложности складывания.
Если вы уже ознакомились с базовыми формами оригами и их взаимосвязями тогда начнём (если нет, то хотя бы просто посмотрите что это).
Колличество схем оригами на сайте постоянно растёт поэтому довольно сложно определиться с выбором для начинающего оригамиста. В дальнейшем планируется создать ранжировку по сложности. Итак, пойдём от простого к сложному, для начала нам нужно заготовить квадратный лист бумаги. Как это сделать?
Альбомный лист складываем как показано на рисунке и отрезаем лишнюю часть. Теперь у нас есть стандартный лист для оригами.
Для того, чтобы вообще понять что такое оригами и потренироваться гнуть бумагу по схемам можно начать с чего-нибудь совсем простенького, например, как этот гриб.
Итак, самое простое мы с вами уже собрали, надеемся ни у кого не возникло никаких проблем с чтеним схем. Если у вас не получается или вы не понимаете обозначения, тогда перейдите на страничку условных знаков оригами.
Теперь перейдем к чему-нибудь более сложному. Все мы с вами в детстве делали самолётики из бумаги. Существует огромное множество различных схем складывания самолётиков, на нашем сайте тоже есть ни одна схема. Давайте попробуем собрать одну из них для того что бы научиться правильно понимать условные обозначения в оригами. На случай если мы что-то вдруг не сможем понять, там есть видео которое можно всегда посмотреть и сравнить со схемой. Итак, оригами самолётика.
Итак, самолётик из бумаги мы с вами уже сложили. Что попробовать дальше? Продолжаем идти дорогой от простого оригами к сложному.
Очень сложная для восприятия для начинающих схема двойного треугольника в оригами, поэтому давайте с вами попробуем сложить по схеме рыбку скалярию из бумаги.
Если не получается сложить рыбку, перейдите на схему двойного треугольника, там есть другие варианты схем.
Теперь вы уже многое знаете и умеете. Можно теперь сложить красивую бабочку из бумаги, сложенную на основе базовой формы катамаран.
Продолжаем двигаться дальше от простого к сложному и заглянем в другой раздел подвижное оригами. Подвижное оригами как вы уже, наверное, догадались — это оригами в котором что-то шевелится. ТИнтересны такие фигурки как говорящая лиса, одевающаяся на пальцы, прыгающая лягушка, которая на самом деле прыгает при нажатии на неё, квакающая лягушка, голова лягушки которая открывается и закрывается при этом громко хлопая(к сожалению даддой схемы пока нет на сайте, но зато нами отснято видео по которому можно её сложить). Советую начать всё-же с квакающей лягушки, но так как наша страничка посвящена схемам мы с вами будем складывать прыгающую лягушку. Не забываем подглядывать в видео если что-то не получается.
Теперь вы готовы самостоятельно выбрать то что вам складывать. Зайдите в один из разделов оригами и выберите понравившуюся вам схему, только не выбирайте сильно сложные. Всё-же советую первое время обращать внимание на те схемы где присутствует видео, для того, чтобы была возможность подсмотреть в случае возникновения проблемы.
Складывайте из бумаги с удовольствием, приятного вам отдыха и успехов в оригами!
Как составить схему предложения: основные виды с примерами
Раз вы тут оказались, наверняка вы школьник, которому надо составить схему предложения. Это стандартное домашнее задание. Схема обычно делается в рамках синтаксического разбора предложения, но бывает и отдельно.
Предлагаю пройти тест – ответить на пять вопросов по схеме предложения.
[quiz-cat id=”2243″]Ну как, что получили? А теперь объяснения.
Алгоритм составления схемы предложения
- Внимательно прочитайте предложение.
- Найдите подлежащее и сказуемое – грамматическую основу предложения. Грамматических основ может быть и несколько, в этом случае предложение сложное. Подчеркните подлежащее одной чертой и сказуемое двумя чертами.
- Определите, простое или сложное предложение.
- Обозначьте границы предложений вертикальными черточками. Отметьте границы простых предложений.
- Для сложных предложений определите союзную связь: сложносочиненное или сложноподчиненное предложение. Сочинительный или подчинительный союз.
- Выделите деепричастный и причастный оборот, если есть.
- Найдите второстепенные члены предложения. Подчеркните их так:
- определение – волнистая линия
- дополнение – пунктир;
- обстоятельство – точка, тире, точка, тире;
- деепричастный оборот – точка, тире, точка, тире, выделяется с двух сторон вертикальными чёрточками;
- причастный оборот – волнистая линия, выделяется с двух сторон вертикальными чертами.
Графические обозначения
Главное предложение обозначается квадратными скобками, а придаточное – круглыми.
Настя сказала, что она пошла домой.
[-=],(что…).
Графические обозначения в схемеЕще примеры с круглыми и квадратными скобками к схемам на рисунке. Все это сложноподчиненные предложения:
Настя шла и молилась, чтобы мама ее не ругала.
[-==],(чтобы…).
Когда Настя засобиралась домой, пошел снег.
(Когда…),[=-].
В том городе, где находится дом Насти, пошел снег.
[…,(где),=-].
Схема простого предложения
А теперь вернемся к простым предложениям. Начнем с самого простого:
Настя шла.
[-=].
Это простое предложение, проще некуда. Нераспространенное, так как в нем есть только подлежащее и сказуемое. Двусоставное, так как оба – и подлежащее, и сказуемое – есть.
Вот это уже распространенное предложение, так как помимо главных членов, есть второстепенный член:
Настя шла домой.
[-=…].
Приведу также примеры односоставных предложения. В них присутствует только один член – либо подлежащее, либо сказуемое. Первое предложение – назывное, главный член – подлежащее:
Снег.
[-].
Вот безличное односоставное предложение, где главный член – сказуемое:
Вечереет.
[=].
Вот определенно-личное предложение, в котором главный член – сказуемое.
Желаю тебе добра.
[=…].
Но все эти детали (безличное, неопределенно-личное) в школе запоминать не надо, главное указать подлежащее со сказуемым. Что такое односоставные предложения вообще-то проходят в каком-то классе, но безличные они или неопределенно-личные, по-моему, уже не проходят.
Бывают еще простые и сложные сказуемые. Простое:
Настя собиралась домой.
[-=…].
Далее сложное глагольное. Здесь глагол один – “собиралась идти”. Не дайте ввести себя в заблуждение двумя словами, из которых он состоит:
Настя собиралась идти домой.
[-=…].
И сложное именное:
Настя рада быть полезной.
[-=…].
Схемы с обращениями и вводными словами
Настя, иди уже домой!
[|O|,…]!
В схеме обращения обозначаются O и обособляются вертикальными черточками. Обращения не являются членами предложения, потому и обособляются черточками. Они могут быть расположены в любом месте предложения. В схему обычно переносятся стоящие при них знаки препинания.
Пожалуйста, Настя, иди уже домой!
[…|O|,…]!
Вводные слова тоже не являются членами предложения и обособляются вертикальными линиями. Обозначаются они ВВ:
Кажется, Насте пора домой.
[|ВВ|,…].
Схемы с причастными и деепричастными оборотами
“Выйдя из дома” – деепричастный оборот ДО:
Выйдя из дома, Настя внезапно остановилась.
[|ДО|,…].
“постепенно сгущавшийся” – причастный оборот ПО:
Туман, постепенно сгущавшийся, делал передвижение Насти трудным.
[X,|ПО|,…].
Крестиком тут обозначено главное слово “туман”. Туман какой? Постепенно сгущавшийся. От него задается вопрос, потому это главное слово.
Деепричастный оборот может стоять в любом месте:
Настя, выйдя из дома, внезапно остановилась.
[…|ДО|,…].
Схемы с прямой речью
В таких схемах обозначаются границы, прямая речь, слова автора и стоящие при них знаки препинания. Например:
“Настя, или домой!” – громко сказал кто-то.
«[П!]»- [а].
Кто-то сказал: “Настя, или домой!”.
[A]:«[П!]»
Кто-то сказал: “Настя, или домой!” – и Петя не возразил.
[A]:«[П!]» – [a].
Схема сложного предложения
В сложносочиненном предложении обе части равноправны, ни одна не подчинена другой.
Вот сложносочиненное предложение с союзом “а”:
Настя шла, а туман застилал ей дорогу.
[-=],а [-=].
А вот сложносочиненное предложение с союзом “и”:
Снег падал, и ветер усилился.
[-=],и [-=].
Сложносочиненное бессоюзное:
Снег падал, темнело.
[-=],[=].
В сложноподчиненном предложении есть главное и придаточное, поэтому иногда схемы составляют вертикально, если уровней зависимости несколько. Главное – в квадратных скобках, зависимое – в круглых:
Насте рассказали, что ее ждет испытание.
[-=],(что…).
Если еще уточнить, какое именно испытание ее ждет, получится три уровня:
Насте рассказали, что ее ждет испытание, которое определит ее жизнь.
[-=],(что…),(которое…).
Тут обе пары круглых скобок выглядят одинаково, тогда как на деле “какое испытание” – это второй уровень вложенности. Сначала “что ждет” – “испытание”. Потом “какое” – “которое определит”:
[-=],
(что…),
(которое…).
Но не всегда несколько придаточных предложений означают, что они все на разных уровнях. Два придаточных могут быть второстепенными по отношению к главному, но абсолютно равны между собой:
Когда Петя подошел, Настя прищурилась, чтобы лучше рассмотреть его.
(когда…),[-=],(чтобы…).
Настя прищурилась когда? Когда Петя подошел.
Настя прищурилась зачем? Чтобы лучше рассмотреть его.
Оба придаточных относятся к “Настя прищурилась” – уточняют зачем и когда она это сделала. А не одно придаточное уточняет другое придаточное. Оба равноправны, так как каждое уточняет главное:
[-=],
(когда…), (чтобы…).
Схема сложносочиненного предложения – примеры
Составление схемы сложного предложения необходимо не только для того, чтобы выполнить данную часть задания по синтаксическому разбору, но и для того, чтобы понять, по какому принципу построено предложение.
Кроме прочего, это необходимо еще и для того, чтобы все знаки препинания были расставлены верно. Все это касается, конечно, и сложносочиненного предложения, составление схемы которого может представлять определенные трудности для учащихся. Чтобы составить его схему правильно, нужно учесть ряд важных моментов.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем русского языка и литературы — 27 лет.
Схема сложносочиненного предложения: этапы ее составления
Для начала нужно определиться с тем, сколько частей входит в разбираемую синтаксическую единицу и каким образом они связаны, то есть найти все грамматические основы, а также сочинительные союзы, которые служат для связи простых предложений в общее сложное.
Сочинительные союзы могут быть не только простыми, но и составными, так что их части могут находиться в разных частях предложения.
Когда будут определены границы частей сложносочиненного предложения, можно приступать к составлению схемы.
Поскольку все части в этой синтаксической единице равноправны, они обозначаются квадратными скобками. При этом и знак препинания, и союз выносятся за скобки.
Примеры составления схемы сложносочиненного предложения
Проще всего данный материал рассмотреть на примерах – несколько будут приведены ниже.
Она старалась не плакать, но чувства были слишком сильными. В этом предложении две грамматические основы, а значит, две части, которые связаны между собой сочинительным союзом но, перед которым стоит запятая. Следовательно, схема данного предложения будет выглядеть следующим образом: […], но […]. Это самый простой пример.
Вот более сложное предложение. Фиалки уже отцветали, а на смену им готовились прийти яркие и ароматные тюльпаны – и разносящий по степи их запах ветер был первым предвестником перемен. В данном предложении три грамматические основы, а значит, три равноправные части. При этом во второй использован сочинительный союз а, перед которым стоит запятая, а в третьем – сочинительный союз и, перед которым стоит тире.
Следовательно, схема этого сложносочиненного предложения будет такой: […], а […] – и […].
Рассмотренные примеры сложносочиненных предложений со схемами показывают, как важно внимательно подходить к вопросу их составления.
Составление схемы сложносочиненного предложения: важные моменты
Сложносочиненные предложения с разрывом конструкции – большая редкость, поэтому при составлении схемы следует быть внимательнее: возможно, речь идет не о разрыве конструкции, а о двух разных частях предложения.
Обычно в сложносочиненном предложении используется такой знак препинания, как запятая, однако если оно достаточно объемное, то между несколькими частями может ставиться и точка с запятой. Тире же хоть и используется, но все же достаточно редко.
Что мы узнали?
Непосредственно перед составлением схемы сложносочиненного предложения необходимо проделать подготовительную работу по определению количества частей, из которых состоит синтаксическая единица. Кроме того, необходимо определить, с помощью каких синтаксических союзов эти части связаны и какие между ними стоят знаки препинания.
Поскольку части сложносочиненного предложения равноправны, на схеме они обозначаются квадратными скобками, между которыми ставится соответствующий знак препинания, а после него – сочинительный союз. При составлении схемы очень важно проявить внимательность и правильно определить гр
Модульное оригами из треугольников: схема и пошаговая инструкция
Существует несколько видов модулей-оригами из бумаги, но треугольники пользуются наибольшей популярностью. Только они позволяют создавать самые разнообразные модели на базе одной и той же «строительной» единицы. Фантазия оригамистов ничем не ограничена – из миниатюрных треугольников можно складывать цветы, животных, вазы и архитектурные объекты, размером от человеческой ладони до двух метров и более.
Что такое треугольный модуль
В основе элемента лежит прямоугольник, размером от 1/4 до 1/36 альбомного листа (формат А4). Соединяются готовые модули за счёт выступающих «уголков» и глубоких «карманчиков», по принципу штекерного разъёма.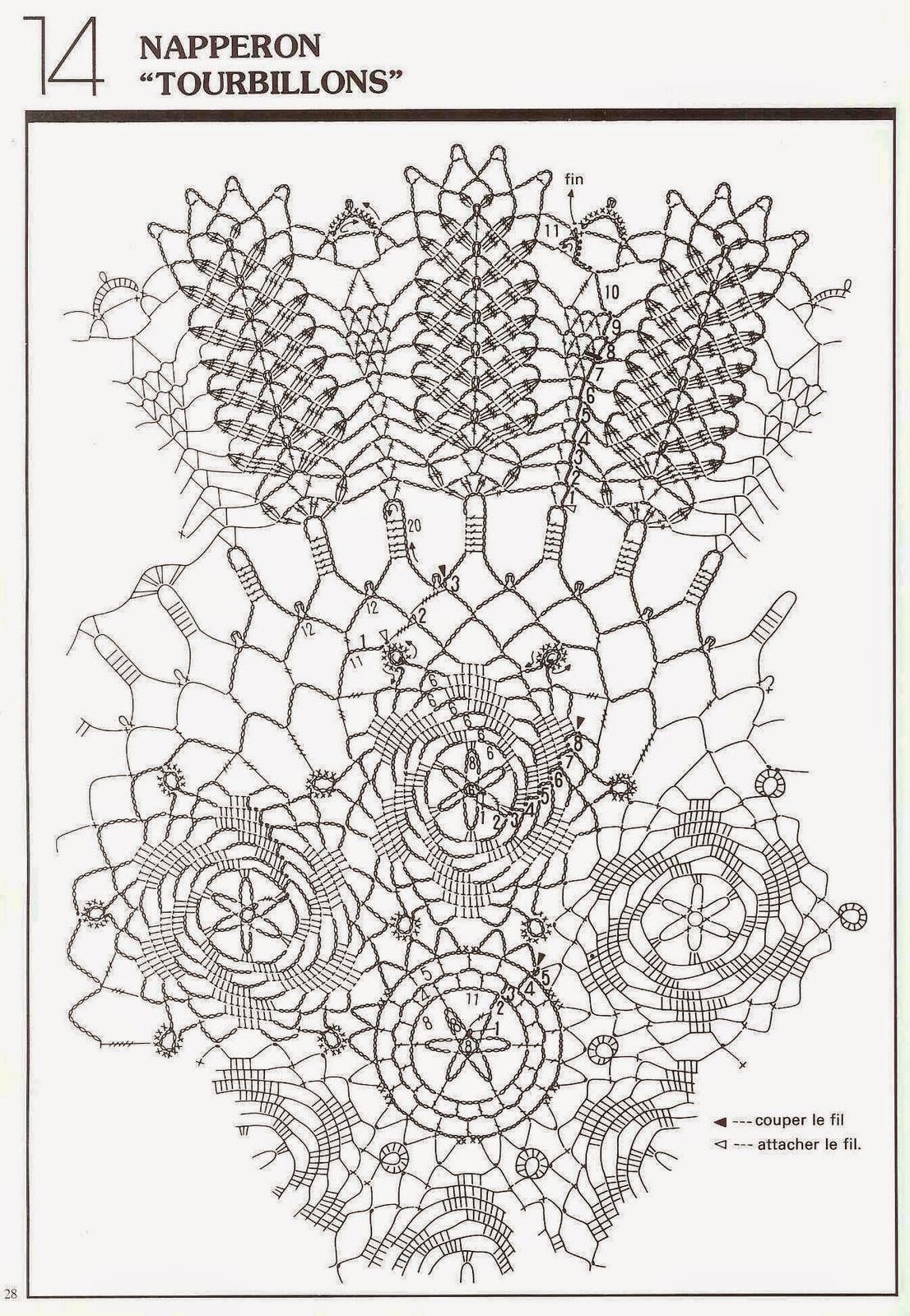
Плотное прилегание деталей обеспечивает прочность конструкции, но для большей надёжности лучше дополнительно «посадить» их на клей.
Перед тем как делать треугольники для модульного оригами, необходимо нарезать прямоугольные заготовки определённого размера. Допустимо одновременное использование нескольких «калибров»: более крупного для основных объёмов и мелкого – для изящного декора. Разделить лист на модули можно, опираясь на базовую форму «Дверцы». Для самого ходового элемента 1/16 потребуется:
- Сложить лист пополам в продольном направлении.
- Раскрыть.
- Каждую половинку сложить к центральной линии.
- Раскрыть заготовку и повторить те же действия в поперечном направлении. В результате лист будет поделен на 16 частей, размером 7,4х5,3 см.
Получить 1/32 несколько сложнее. Лист А4 сначала в поперечном направлении делят вдоль центральной оси, а затем каждую половину складывают в четыре раза. Получается вдвое больше полос, чем в предыдущем случае.
Для продольного направления действия те же, что и при разметке модуля 1/16. В результате образуются прямоугольники, размером 5,3х3,7 см. Нарезать заготовки лучше всего канцелярским ножом, подложив под лист доску, ДВП или специальный макетный коврик.
Получить прямоугольники 1/32 можно и другим способом:
Модуль-треугольник
Сложить из прямоугольной заготовки треугольную деталь не составит никакого труда. Единственное «но» – таких элементов потребуется очень много, в среднем, на одну фигурку высотой 25 – 30 см около 1000 штук. Опытные мастера советуют по мере возможности пополнять запасы деталей, занимаясь другими делами. Например, во время просмотра любимого сериала или прогулки с ребёнком. После некоторой тренировки, складывать треугольники получается, даже не глядя.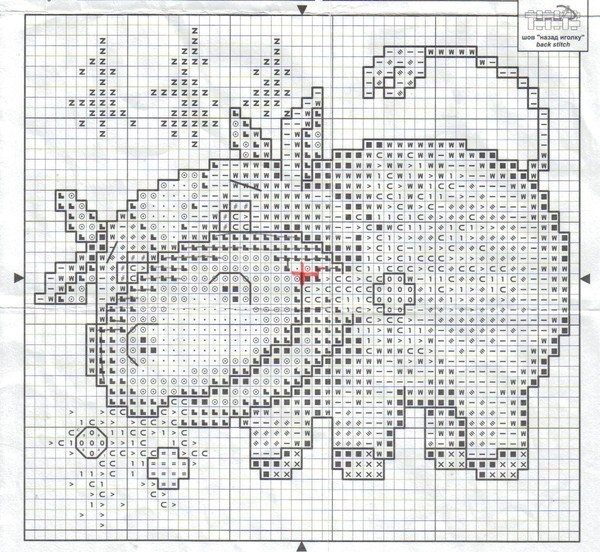
Пошаговая инструкция:
- Располагаем исходный прямоугольник длинной стороной к себе.
- Складываем пополам сверху вниз (это важно, поскольку свободный край должен «смотреть» на нас). Заготовку сгибаем вдвое поперёк, чтобы обозначить у неё середину. Раскрываем.
- Правый и левый край опускаем вниз, выравнивая по центру. Переворачиваем.
- Подгибаем внешние уголки заготовки.
- Подворачиваем нижнюю часть до линии основания треугольника.
- Складываем фигуру пополам «долиной».
В итоге получаем классические треугольники для модульного оригами:
Существует несколько типов соединений модульных элементов. Они зависят:
- от выбора стороны, которой одна деталь соединяется с другой;
- от взаимного расположения «уголка» и «карманчика».
Азбука модульного дела:
- У треугольного модуля есть две коротких стороны, расположенных напротив углов в 60° и одна длинная – напротив прямого. На рисунке они обозначены соответственно, КСН и ДСН.
- Соединение на коротких сторонах (КСН).
- То же, но на длинных (ДСН).
- «Змейка», когда модульные элементы соединяются один в один.
- Классическое соединение «две длинных стороны и одна короткая».
- «Все короткие».
- У треугольного модуля есть две коротких стороны, расположенных напротив углов в 60° и одна длинная – напротив прямого.
На рисунке они обозначены соответственно, КСН и ДСН.Три модели в технике модульного оригами
Начинающим мастерам не всегда знакомы тонкости «бумажного искусства». Главное при сборке оригами из модулей-треугольников, как и в других видах рукоделия: вышивке, плетении или вязании, не спешить и на каждом этапе чётко следовать схеме. Тогда работа сразу получится аккуратной и прочной, не требуя переделок. Есть и другие значимые моменты:
- Модули необходимо складывать очень точно, иначе изделие будет перекошенным и неряшливым. Чем меньше размер сборочных элементов, тем тоньше выбирают бумагу для них.
- Если «карманчики» трудно раскрываются, можно воспользоваться зубочисткой.
- Начинать знакомство с модульным оригами лучше с лёгких моделей, постепенно переходя к более сложным.
- Склеивание элементов изделия поможет сохранить его на длительный срок и убережёт от разрушения при падении.
- Готовые работы стоит покрыть прозрачным лаком для дерева. Это – хорошая защита от пыли и выцветания, а также возможность делать влажную уборку.
Сова
Удачная модель для тех, кто только начинает знакомиться с техникой складывания оригами из маленьких треугольников. Для неё понадобится всего 106 синих модулей и 24 розовых.
Схема «Совы»:
Сборка ведётся на длинных сторонах. 1-й ряд состоит из 16 синих элементов. Начиная со 2-го, добавляем розовые детали для «манишки» совы (12+4).
Общее число элементов в каждом ряду одинаковое. Но соотношение по цветам разное.
3-й ряд: 10 синих и 5 розовых деталей.
4-й ряд: 8 синих и 6 розовых.
Далее модули распределяются в обратной последовательности. Для предпоследнего ряда берём 16 синих деталей, для последнего – 15.
Собрав сову, делаем её характерные «ушки». Они состоят из 3-х деталей, которые крепятся на последний ряд, по тому же принципу, что и остальные. Затем приклеиваем птице глаза и нос из розового модульного элемента.
«Сова» яркого сказочного окраса украсит дом на Хэллоуин или другой тематический праздник. Также она будет эффектно смотреться в детской.
Китайский мини-дракон
Следуя принципу постепенного усложнения моделей, после сверх-простой совы как раз можно перейти к популярному на востоке символу водной стихии. Дракон в Китае издавна был связан с культом плодородия, без его изображений не обходился ни один ритуал вызывания дождя. Кроме того, этот мифический персонаж обозначал принадлежность к высшим слоям общества. Его изображениями разрешалось украшать одежду только аристократии, простолюдинам же, подобная «вольность» была недоступна.
Для того, чтобы сделать мини-дракона, понадобится 515 бумажных треугольников-оригами 1/16:
- 251 синий (С),
- 264 жёлтых (Ж).
Голова
Начинаем работу с головы. Схема её сборки:
Двигаемся от «подбородка» вверх.
| Ряд | Количество модулей |
| 1 | 3 С |
| 2 | 4 С |
| 3 | 3 С |
| 4 | 4 С |
| 5 | 5 С |
| 6 | 4 С |
| 7 | 1 С+1 Ж+1 С+1 Ж+1 С |
| 8 | 6 С |
| 9 | 5 С |
| 10 | 6 С |
Сборку производим сверху вниз. Завершив 10 ряд, делаем шипы, венчающие драконью голову. Собираем их симметрично по схеме, сделав пропуск посредине. Переворачиваем фигуру и слегка изгибаем – голова почти готова. Из красной бумаги вырезаем раздвоенный язык и приклеиваем по центру последнего ряда с изнанки.
Туловище дракона
Гибкое тело мифического животного представляет собой цепочку из жёлтых и синих деталей. Вначале их три: С+Ж+С. К первой жёлтой детали в следующем ряду добавляем ещё две, надевая на каждый уголок.
Затем вновь повторяем начальное расположение треугольников и так продолжаем, пока не наберём примерно 88 рядов. Для тела потребуется 176 синих и 262 жёлтых элемента. Закончив сборку, к голове с обратной стороны в районе глаз добавляют два синих крепёжных модуля.
Изготавливаем 4 лапки из 5 синих деталей. Присоединяем заготовки к туловищу в точках опоры. Предварительно изгибаем его, наподобие американских горок.
Мини-дракон готов!
Лебедь
Это одна из самых красивых и востребованных моделей. Лебедь-оригами из модульных треугольников легко превращается в элегантную вазу для сухоцветов, хотя и сам по себе он великолепен.
Для двухцветной модели, представленной в следующем видео-уроке, понадобится 1522 модуля, размером 1/32:
- 1322 белых,
- 180 розовых.
Историческая справка
Под модульным оригами чаще всего подразумевают именно фигуры из маленьких треугольников. Однако существуют ещё шары-кусудамы и многогранники из так называемых «модулей Сонобе.» Обе разновидности родом из Японии. Кусудама – бумажный шар из нескольких сшитых или склеенных между собой секций, известна со времён Средневековья. Её наполняли ароматными травами, выделявшими целебные эфирные масла, и развешивали в доме для защиты от инфекционных заболеваний, а также создания успокаивающей атмосферы.
Многогранники из модулей в виде изогнутого особым образом параллелограмма, были разработаны в 1960-х годах японским оригамистом Мицунобу Сонобе и названы в его честь. Идею мастер, скорее всего, позаимствовал у своего предшественника Хаято Охоко, в 1734 году впервые описавшего и представившего схему трёхмерного куба из нескольких одинаковых элементов.
Оригами из треугольных модулей – изобретение китайских мастеров. Его истоки точно неизвестны, но западному миру пришлось познакомиться с этой уникальной техникой при весьма печальных обстоятельствах. В 1993 году на борту грузового судна Golden Venture в Соединённые Штаты прибыли 286 нелегальных эмигрантов из Китая. «Новая родина» встретила их неласково. Когда корабль сел на мель неподалёку от нью-йоркского пляжа Рокуэй-Бич, пассажиры попытались добраться до «земли обетованной» вплавь, причём 10 из них утонули. Остальные нелегалы были арестованы Службой иммиграции и натурализации (INS) и разбросаны по тюрьмам в разных концах Америки.
В ожидании ответа на просьбу о предоставлении убежища, китайские заключённые коротали время за национальными видами рукоделия, в том числе и оригами, которое на пиньине называется «жэжи». В процессе работы нелегалы изобрели треугольные модули, создавая из них масштабные фигуры: вазы, лебедей, ананасы и корабли. Вместо обычной бумаги использовали обложки старых журналов и газет. Позднее, когда техника получила распространение, для модульных элементов нередко брали китайские банкноты.
Скульптуры в технике модульного оригами заключённые дарили тем, кто оказывал им поддержку или продавали, чтобы собрать средства на юридические услуги. Часть их представлена на передвижной выставке «Полёт свободы», организованной Американским иммиграционным центром.
Какие ещё бывают треугольники-оригами
Треугольные модули – первое, что приходит на ум, когда речь идёт о технике оригами. Но существуют и другие элементы с аналогичным названием, с которыми желательно познакомиться, чтобы не путаться в понятиях.
«Двойной треугольник»
Китайские модули-оригами иногда путают с популярной базовой фигурой, не имеющей к ним никакого отношения. «Двойной треугольник» или «Водяная бомбочка» применяется в классическом японском бумагоделии, как основа для многих известных моделей. Среди них «Рыбка», «Лягушка», «Кролик» и так далее.
Складывается базовый треугольник оригами по следующей схеме:
Солдатское письмо
Знаменитые «фронтовые треугольники», которые посылали бойцы с передовой во время Великой Отечественной войны, как ни удивительно, тоже сложены в технике оригами. Такой способ позволял обходиться без конверта – адрес писали на внешней стороне листа, а сообщение на внутренней. При этом письмо не мялось и рвалось, каждая его строчка была сохранена для близких людей, с нетерпением ожидавших весточки.
Солдатские треугольники дарили радость, служили лучшим свидетельством того, что их автор жив. А вот письма в настоящих конвертах отправляли только официальные инстанции, извещая о гибели или пропаже без вести. Чтобы проникнуться атмосферой тех лет и сберечь память о подвиге народа в борьбе с немецким нацизмом, «Солдатские треугольники-оригами» часто изготавливают ко Дню победы.
Вязание связок спицами по схемам. Сложные узоры
Вязать спицами схемы косичек не представляет особой сложности, поэтому мастера часто применяют такие схемы при изготовлении различных изделий. Используйте шлейки различной конфигурации для вязания детских вещей, свитеров и кардиганов, шарфов и шапок, ободков и носков, варежек и сумок.
Для начинающих квилтеров следует начинать с образца. Если вы научитесь плести простую одинарную косу, то ее можно будет использовать при создании более сложных жгутов.Для того, чтобы научиться плести спицами разнообразные плетения, вы можете придумать свои собственные, ведь их огромное разнообразие.
Простая тесьма
Чтобы научиться вязать жгуты, необходимо понимать основной принцип вываживания и скрещивания петель в простой тесьме. Возьмем для примера косу из трех петель. Для того, чтобы получить такой узор, нужно связать образец со спицами 14 петель. Из них две — кромочные, а оставшаяся часть узора. Первые три вяжите изнаночными, затем снова 6 лицевых и 3 изнаночных.Таким образом промазывают все передние ряды. С обратной стороны петли выполнены так, как выглядят. После провязанных 6 рядов начинается скрещивание петель для образования нужной нам косы.
Для дальнейшего вязания жгутов спицами по схеме вам понадобится вязание или простая английская булавка. Первые три лицевые петли снимать, не промазывая на булавке. Начинает вязание с 4-6 петель. После того, как они оказались на правой спице, промазывается 1–3 петли, а оставшиеся три — другими.Затем снова промазывается 6 рядов, как вы видите петлю.
Рекомендуем
Значки рейтинга в серебре. Оценка старинных икон фото
Старые православные иконы вызывают большой интерес у коллекционеров во всем мире. Это не только объект эстетического и духовного наслаждения. Старые иконы — беспроигрышное вложение. Как особый вид антиквариата, они высоко ценятся на рынке, и …
Связанные крючком купальники крючком
Так что вы хотите отличаться от других! Итак, вы хотите быть неотразимой! Так хочется видеть на фигуре восхищенные взгляды и слышать за спиной восторженные вздохи.Хотя это случается редко, женщина открыто признает это. и не надо! Вам просто нужно связать купальник крючком, так что & hellip …
Заключение
Спортивные гимнастки, для которых спорт — это жизнь, львиную долю времени нужно уделять тренировкам и участию в соревнованиях. За этот период успевают снести более десятка гимнастических трико. Так что мама юных спортсменок кон …
Количество рядов в высоту вязальщиц может варьироваться по желанию. Также можно изменить количество петель в большинстве КО: от 2 до 5 в зависимости от толщины нити.Если пряжа толстая, перекрещивание будет выглядеть грубым, если петли задействовать много. Для тонких ниток их можно набрать больше.
Составление карт
Жгуты спиц могут быть сложными, поэтому при их составлении нужно нарисовать схему, чтобы не отклониться от правильного положения петель. Рассмотрим следующий пример. Начинает любую работу с оригинальным набором. Для такой пробы набрано 19 петель, включая кромочную. Вяжем 2 см., 6., 1 изн., 6. 2 см. Первый и последний край.Промазывают 4 ряда видимой петлей. Затем сделайте скрещивание 6 лицевых. Промазывают 4 серии это как смотреть шлейф.
Затем начните обрабатывать каждую косичку отдельно. Для этого каждая пара из нескольких уже пересекает 3-х петли, пока вы не дойдете до 4-го пересечения. Затем закончите проводку перекрещивания уже большой части косы из 6 петель. Затем это повторяется снова.
Сложные связки
Вываживание узора «Связки» спицами схемы не допускается только в одном направлении.Рисунок может быть сложным и представлять собой пересечение в разных направлениях. В следующем примере вы можете увидеть, как 15 лицевых петель образуют красивую схему переплетения с той или иной стороны. После набора петель (нужно 23 петли) промазывают перед рядом и в конце три изнаночные петли. Центральная 15 — лицо.
Сделав ряд 4, начинайте переход. В зависимости от направления обвязки три петли снимаются на булавке либо перед образцом, либо с обратной стороны.Выключение в первый раз начинается со снятия штифта обратно. Провязать еще 4 ряда, сделав снятие штифта перед изделием. Тогда косы-ленты будут направлены в другую сторону. Это продолжается поочередно. Схемы вязания узоров «Связки» вяжите аккуратно, чтобы не допустить ошибок, иначе изделие будет выглядеть неаккуратно.
Декорирование вязаных изделий
С помощью таких интересных элементов можно не только связать основной узор вещей, но и украсить их отдельные элементы.Например, на шапке можно связать повязку на голову, на свитере несколько центральных ремней по центру спереди. Очень красивый дизайн бокового разреза платья или кардигана, который вы можете просмотреть на фото ниже.
Вязание косичек на спицах по описанию и схемам происходит несложно, так что попробуйте и у вас все получится. Впоследствии вы сможете придумывать шаблоны, потому что это очень увлекательно.
Математически сложные схемы — Большая химическая энциклопедия
Это краткое обсуждение подчеркивает роль анализа уязвимости цели в более широком и более сложном процессе системного анализа, связанного с эффективностью боеприпасов или повышением живучести нашего собственного оборудования.Но, хотя анализ уязвимости цели является лишь элементом более сложной схемы вещей, он сам по себе довольно сложен и, в свою очередь, должен учитывать или принимать данные из других сложных дисциплин, таких как терминальная баллистика и математическая теория статистики. Поэтому структура анализа уязвимости цели обсуждается далее … [Pg.300]Одна проблема для кинетиков состоит в том, что только относительно небольшое увеличение сложности кинетической схемы приводит к дифференциальным уравнениям, которые нельзя интегрировать простым способом, чтобы дать управляемое аналитическое выражение.Когда это происходит, дифференциальные уравнения должны быть решены путем численного интегрирования или компьютерного моделирования. Это математическое ограничение использования выражений интегрированной скорости, которое не проявляется в кинетической схеме. Типичными математически сложными схемами являются … [Pg.81]
Эти математически сложные кинетические схемы следует сравнивать с математически простыми схемами … [Pg.81]
Как отмечалось ранее, реальные мембраны характеризуются неоднородностью профили свободной энергии для двухслойной проницаемости.Следовательно, моделирование молекулярной динамики использовалось для обработки движения растворенного вещества через двухслойную мембрану. Эти расчеты точно воспроизводят экспериментально оцененные значения диффузии 143]. Однако, поскольку этот подход математически сложен, он применялся только для проникновения относительно небольших молекул. Приближенные методы были разработаны на основе простой кинетической схемы для диффузии растворенных молекул M в системе с четырьмя отсеками … [Pg.2988]
В качестве демонстрации того, как эти изменения могут быть смоделированы математически, упрощенная пятиреакционная Схема попугая, описанная в разделе 7.3.4 (v), для краткости взят в качестве примера. Однако общий подход легко применим к более сложным схемам. [Pg.716]
Хорошо известно, что ввиду явной математической сложности, с которой мы сталкиваемся, когда пытаемся решить уравнение Шредингера для простейших молекулярных систем (уже для одноэлектронного катиона H [9]), мы должны сосредоточиться на разработке вычислительно управляемых, но надежных схем аппроксимации, основанных на различных модельных гамильтонианах. Даже если пренебречь релятивистскими эффектами и заморозить движение ядер с помощью приближения Бома-Оппенгеймера [10], проблема все равно остается слишком сложной для любой системы, имеющей более двух электронов.Именно по этой причине почти все квантово-механические трактовки электронной структуры молекул основаны на размерных моделях. [Pg.117]
Математическая сложность реакций на неоднородных поверхностях обычно не позволяет получить компактное аналитическое выражение даже для этой простой схемы реакции. Однако точную оценку задействованных интегралов можно получить с помощью численного интегрирования. В качестве метода численного интегрирования было выбрано интегрирование Монте-Карло (MCI) из-за его простоты, точности и гибкости.MCI считается методом выбора для работы с такими сложными функционалами [23], кроме того, он легко расширяется, так что любое количество адсорбированных частиц можно легко рассматривать в более сложных реакционных системах [16]. [Pg.344]
Когда спектральная интерпретация будет завершена и химическая природа присутствующих частиц будет идентифицирована, внимание будет обращено на структуру и состав образца. В этом разделе описаны методы, используемые для определения такой информации из данных XPS и AES.Акцент делается на предоставлении карты маршрута. или руководствоваться различными возможными подходами с глубиной математической сложности, достаточной для решения практических задач, но не обязательно строгой во всех отношениях. Файл. Схема следует логике блок-схемы на рис. 6. Количественная оценка данных от образцов, которые являются однородными как по горизонтали, так и по глубине, обсуждаются в разделе. 1.1. Модификации, необходимые для учета влияния боковых колебаний и вариаций глубины, рассматриваются в Разделах 3.2 и 3.3. соответственно. [Стр.182]
Подводя итог оценке коэффициентов активности трехкомпонентных и многовидовых жидкостей, мы видим, что математическая и вычислительная сложность возрастает, но, используя только легкодоступные двоичные данные, мы можем сделать справедливую оценку наблюдаемого поведения. Более сложные схемы более точны и требуют больше времени, но их легко реализовать в компьютерных программах. [Pg.155]
Не существует общей явной математической обработки сложных уравнений скорости.В разделе 3.1 мы описываем кинетические схемы, которые приводят к практическому применению интегральных скоростных уравнений в замкнутой форме. В разделе 3.2 рассматриваются многие дополнительные подходы, как экспериментальные, так и математические, к этим сложным системам. Глава завершается комментариями по разработке кинетической схемы сложной реакции. [Стр.59]
В этой главе рассматриваются три аспекта кинетики, относящиеся к схемам реакций с промежуточными соединениями. В первом представлено несколько схем реакций, которые протекают в два или более этапов, причем первоначальный акцент делается на тех, дифференциальные уравнения скорости которых могут быть решены точно.Это решение дает математически строгие выражения для зависимостей концентрации от времени. Вторая ситуация состоит из группы, упомянутой ранее, в которой приблизительное решение — стационарное или какое-то другое — действительно в допустимых пределах. Третья и наиболее общая ситуация — это ситуация, в которой семейство одновременных дифференциальных уравнений скорости для сложной многоступенчатой реакции … [Pg.70]
Кинетическая информация получается путем мониторинга во времени какого-либо свойства, такого как поглощение или проводимость, которая может быть связана с постепенным изменением концентрации.Эксперимент устроен так, что переход от одного положения равновесия к другому не очень велик. С одной стороны, небольшой размер регулировки концентрации требует чувствительного обнаружения. С другой стороны, это приводит к значительному упрощению математики, поскольку повторное уравновешивание одностадийной реакции будет следовать кинетике первого порядка независимо от формы кинетического уравнения. Мы вскоре рассмотрим обработку данных для этого и для более сложных кинетических схем. [Стр.256]
Структура и математические выражения, используемые в моделях PBPK, значительно упрощают истинные сложности биологических систем. Однако, если поглощение и утилизация химического вещества (веществ) адекватно описано, такое упрощение желательно, поскольку данные для многих биологических процессов часто недоступны. Упрощенная схема снижает величину совокупной неопределенности. Следовательно, адекватность модели имеет большое значение, и проверка модели имеет важное значение для использования моделей PBPK при оценке риска.[Pg.98]
Создание строгой математической кинетической модели, основанной на схеме на рисунке 3.1, очень сложно (7). Чтобы выяснить механизм реакции, сложность механизма реакции может быть уменьшена на основе следующих трех предположений … [Стр.29]
Независимо от того, является ли схема прогнозирования простой диаграммой, формулой или сложной численной процедурой, существуют три основных элемента, которые необходимо учитывать: метеорология, выбросы из источников и химические взаимодействия в атмосфере.Несмотря на разнообразие доступных методологий соотнесения выбросов с качеством окружающего воздуха, существует два основных типа моделей. Те, которые основаны на фундаментальном описании физики и химии, происходящих в атмосфере, классифицируются как априорные подходы. Такие методы обычно включают математическую обработку метеорологических и химических процессов и, кроме того, используют информацию о распределении исходных выбросов. Другой класс методов включает использование апостериорных моделей, в которых эмпирические зависимости выводятся из лабораторных или атмосферных измерений.Эти модели обычно довольно просты и обычно тесно связаны с фактическими данными, на которых они основаны. Последняя особенность — основная слабость. Поскольку модели не дают явной количественной оценки причинных явлений, их нельзя надежно экстраполировать за пределы данных, из которых они были получены. В результате апостериорные модели не идеально подходят для задачи прогнозирования воздействия существенных изменений выбросов. [Pg.210]
Сегодня существует установленный набор программных инструментов для выполнения основной задачи, расчета режимов и описания распространения поля.Подходы, основанные на методе конечных элементов (FEM) и конечных разностях (FD), популярны уже давно и могут применяться к сложным задачам. Используются метод волнового согласования, подходы функций Грина и многие другие схемы. Но на самом деле, чем больше преобладают численные методы, тем больше пользователь должен исследовать результаты с физической точки зрения. Современные математические методы, которые позволяют полностью контролировать точность — по крайней мере, если проблема хорошо поставлена, — помогают инженеру-конструктору в этом…. [Pg.246]
Расслабленная комплексная схема — Большая Химическая Энциклопедия
Лин Дж. Х., Перриман А. Л., Шеймс Дж. Р., Маккаммон Дж. А. 2002. Вычислительный дизайн лекарств с учетом гибкости рецепторов по расслабленной сложной схеме. J Am Chem Soc … [Pg.303]Amaro RE, Baron R, McCammon JA (2008) Улучшенная расслабленная комплексная схема для рецепторной гибкости в компьютерном дизайне лекарств. J Comput Aided Mol Des 22 (9) 693-705 … [Pg.11]
Многоуровневые методы, в которых гибкость белка учитывается как минимум на двух независимых этапах протокола стыковки.Это случай расслабленной комплексной схемы (RCS) [52, 53], в которой ансамбль несвязанных целевых структур генерируется с помощью MD, а затем используется для стыковки небольшой химической библиотеки … [Pg.250]
Схема Relaxed-Complex реализует ирформацию выборки простым способом, взяв среднее значение seoiing-значений hgand при стыковке с отдельными периодически извлекаемыми коррформациями. Разработчики RCS наблюдали в первом приложении, что наиболее благоприятные значения оценки были получены от неродных приложений… [Pg.524]
Сообщалось о сильном снижении релаксивности (с 12,8 мМ-1 с-1 до 2 мМ-1 с-1) между pH 6 и 11 для положительно заряженного макроциклического комплекса Gdm (Схема 10), который было объяснено последовательным депротонированием координированных молекул воды.167 Измерения времени жизни люминесценции аналога Yb111 показали, что комплекс имеет три связанных воды при pH 5.5. При pH выше 11 образуется димер с диоксо-мостиковой связью, который больше не имеет связанной воды или групп ОН. [Pg.867]
Продукты термического окисления полиэтиленовых пленок можно охарактеризовать с помощью C FTNMR, кроме того, используя метод спин-решеточной релаксации, можно сделать количественные оценки окисленных функциональных групп.Наблюдение за развитием различных функциональных групп приводит к постулированию гидропероксидов как первичных продуктов окисления, которые подвергаются дальнейшим превращениям в другие производные по сложной схеме. [Pg.695]
Зависимость люминесценции и релаксации от pH показала, что комплексы с европием, гадолинием и лантаном могут быть использованы для МРТ. Позднее эта концепция была подтверждена Frias et al. [8] с использованием близких по структуре комплексов лантаноидов (схема 9).[Pg.93]
Лин, Дж. Х., Перриман, А. Л., Шеймс, Дж. Р., и Маккаммон, Дж. А. (2003) Метод расслабленного комплекса, учитывающий гибкость рецепторов для разработки лекарств с улучшенной схемой подсчета баллов. Биополимеры 68,47-62. [Pg.91]
| Схема VIII имеет форму схемы II, поэтому время релаксации определяется уравнением. (4-15) — обязательно. Однако существует различие между этими двумя схемами в том, что L на схеме VIII также является участником кислотно-основного равновесия. Перенос протона происходит намного быстрее, чем образование комплекса, поэтому кислотно-основная система считается находящейся в равновесии на протяжении всего образования комплекса.Эксперимент можно провести, установив общую концентрацию лиганда, сравнимую с общей концентрацией ионов металла, чтобы раствор не был забуферен. Когда основная форма L лиганда подвергается координации, кислотно-основное равновесие смещается, что приводит к изменению pH. Этот сдвиг pH определяется включением в раствор кислотно-основного индикатора. |
Сообщалось о необычной зависимости от pH для комплекса Gd111 лиганда на основе тетраамида с протяженными некоординирующими боковыми цепями фосфоната (Схема 12). 169,170 Релаксивность увеличивается от pH 4 до 6, а затем снижается до pH 8,5, затем с pH 10,5 снова увеличивается. Система, а также изоструктурные комплексы лантанидов были охарактеризованы различными методами, такими как 31P и 170 ЯМР и измерения флуоресценции.Зависимость от pH может быть объяснена протонирующим равновесием некоординирующих фосфонатных групп, которые могут … [Pg.867]
Дуализирующие комплексы на схемах — проект Stacks
48.2 Дуализирующие комплексы по схемам
Мы определяем дуализирующий комплекс на локально нётеровой схеме как комплекс, который аффинно локально происходит от дуализирующего комплекса на соответствующем кольце. Это не совсем стандартно, но согласуется со всеми определениями в литературе по нётеровым схемам конечной размерности.\ bullet $ дуализируется дуализирующими комплексами, лемма 47.15.8. $ \ квадрат $
Определение 48.2.2. Пусть $ X $ — локально нётерова схема. Объект $ K $ из $ D (\ mathcal {O} _ X) $ называется дуализирующим комплексом , если $ K $ удовлетворяет эквивалентным условиям леммы 48.2.1.
См. Примечания в начале этого раздела.
Лемма 48.2.3. Пусть $ A $ — нётерово кольцо и пусть $ X = \ mathop {\ mathrm {Spec}} (A) $. Пусть $ K, L $ — объекты $ D (A) $.{-n} (K) $ — конечный $ A $ -модуль, см. Алгебра, лемма 10.10.2. Это доказывает, что каноническое отображение
\ [\ widetilde {R \ mathop {\ mathrm {Hom}} \ nolimits _ A (K, L)} \ longrightarrow R \ mathop {\ mathcal {H} \! \ mathit {om}} \ nolimits _ {\ mathcal {O} _ X} (\ widetilde {K}, \ widetilde {L}) \]
в этом случае является квазиизоморфизмом, и доказательство завершено. $ \ квадрат $
Лемма 48.2.4. Пусть $ X $ — нётерова схема. Пусть $ K, L, M \ in D_ \ mathit {QCoh} (\ mathcal {O} _ X) $.+ _ {\ textit {Coh}} (\ mathcal {O} _ X) $, а аффинно $ M $ локально имеет конечную инъективную размерность (см. доказательство), или
$ K $ и $ L $ находятся в $ D _ {\ textit {Coh}} (\ mathcal {O} _ X) $, объекте $ R \ mathop {\ mathcal {H} \! \ mathit {om}} \ nolimits (L, M) $ имеет конечную размерность, а аффинные локально $ L $ и $ M $ имеют конечную инъективную размерность (в частности, $ L $ и $ M $ ограничены).
Доказательство. Доказательство (1). Мы говорим, что $ M $ имеет аффинную локально конечную инъективную размерность, если $ X $ имеет открытое покрытие с помощью аффинного $ U = \ mathop {\ mathrm {Spec}} (A) $, такое что объект $ D (A) $, соответствующий $ M | _ U $ (Производные категории схем, лемма 36.+ _ {\ textit {Coh}} (\ mathcal {O} _ X) $ по производным категориям схем, лемма 36.10.5. Более того, формирование левой и правой части стрелки коммутирует с функтором $ D (A) \ to D_ \ mathit {QCoh} (\ mathcal {O} _ X) $ по лемме 48.2.3 и производным категориям Схемы, лемма 36.9.8 (чтобы убедиться, что здесь используются предположения о $ K $, $ L $, $ M $ и то, что мы только что доказали относительно $ R \ mathop {\ mathcal {H} \! \ Mathit {om}} \ nolimits (K, L) $). Тогда, наконец, стрелка является изоморфизмом Мора по алгебре, леммы 15.91.1, часть (2).
Доказательство (2). Мы рассуждаем, как указано выше. Небольшое изменение заключается в том, что здесь мы получаем $ R \ mathop {\ mathcal {H} \! \ mathit {om}} \ nolimits (K, L) $ в $ D _ {\ textit {Coh}} (\ mathcal {O} _ X) $, поскольку аффинно локально (что допустимо по лемме 48.2.3) мы можем апеллировать К дуализирующим комплексам, лемма 47.15.2. Затем мы, наконец, заключаем Мор по алгебре, лемма 15.91.2. $ \ квадрат $
Лемма 48.2.5. Пусть $ K $ — дуализирующий комплекс на локально нётеровой схеме $ X $. Тогда $ K $ является объектом $ D _ {\ textit {Coh}} (\ mathcal {O} _ X) $ и $ D = R \ mathop {\ mathcal {H} \! \ mathit {om}} \ nolimits _ {\ mathcal {O} _ X} (-, K) $ индуцирует антиэквивалентность
\ [D: D _ {\ textit {Coh}} (\ mathcal {O} _ X) \ longrightarrow D _ {\ textit {Coh}} (\ mathcal {O} _ X) \]
, который снабжен каноническим изоморфизмом $ \ text {id} \ to D \ circ D $.\ mathbf {L} L \ longrightarrow R \ mathop {\ mathcal {H} \! \ mathit {om}} \ nolimits _ {\ mathcal {O} _ X} (R \ mathop {\ mathcal {H} \! \ mathit {om}} \ nolimits _ {\ mathcal {O} _ X} (L , К), К) \]
(с использованием когомологий, лемма 20.38.9 для второй стрелки) является изоморфизмом для всех $ L $, потому что это верно для аффинов посредством дуализирующих комплексов, лемма 47.15.3 2 , и мы уже видели на аффинах, что мы восстанавливаем то, что происходит по алгебре. Утверждение о свойствах ограниченности функтора $ D $ в квазикомпактном случае также следует из соответствующих утверждений леммы 47 Дуализирующих комплексов. {n_ x} (L_ x) \ not = 0 \]
локально постоянна на $ X $.\ пуля [- \ delta (x)]) \]
По построению $ \ delta $ в лемме 48.2.7 это сводит части (1), (2) и (3) к дуализирующим комплексам, лемма 47.16.5. Часть (4) является формальным следствием (3) и (1). $ \ квадрат $
Комплексные числа: Введение
Комплекс Номера: Введение (стр. 1 из 3)
Разделы: Введение, Операции с комплексами, Квадратичная формула
До сих пор вы были сказал, что ты не можешь взять площадь корень негатива число.Это потому, что у вас не было чисел, которые были бы отрицательными после того, как вы возводил их в квадрат (так что вы не могли «вернуться назад», взяв квадрат корень). После возведения в квадрат все числа были положительными. Так ты не мог очень хорошо извлеките квадратный корень из отрицательного числа и ожидайте найти что-нибудь разумное.
Теперь вы можете взять квадратный корень из отрицательного числа, но это предполагает использование нового числа сделать это. Это новое число было изобретено (обнаружено?) Примерно во времена Реформация.В то время никто не верил, что любой «реальный мир» будет найдено применение этому новому числу, кроме упрощения вычислений участвовал в решении определенных уравнений, поэтому новое число рассматривалось как это вымышленное число, придуманное для удобства.
(Но тогда, когда вы думаете об этом, разве не все числа изобретения? Это не похоже на числа растут на деревьях! Они живут в наших головах. Мы сделали их , все up! Зачем не придумывать новый, раз уж он работает нормально с тем, что у нас уже есть?)
Во всяком случае, этот новый номер назывался « и «, означает «воображаемое», потому что «все знали» что и не были «настоящими».(Вот почему вы не могли извлечь квадратный корень отрицательного числа раньше: у вас были только «настоящие» числа; что есть числа без « i » в них.) Воображаемое определяется как:
Тогда:
Теперь вы можете подумать, что умеют:
Но это не делает
смысл! У вас уже есть , у вас есть двух чисел, равных 1;
а именно –1 и +1.А и уже равняются –1.
Поэтому неразумно, что и также будут равняться 1.
Это указывает на важную деталь: имея дело с воображаемым, вы
получить что-то (способность иметь дело с отрицаниями внутри квадратных корней),
но вы тоже что-то теряете (некоторая гибкость и удобные правила
вы имели обыкновение иметь дело с квадратными корнями).В частности, ВЫ ДОЛЖНЫ
ВСЕГДА ДЕЛАЙТЕ ЧАСТЬ i ПЕРВЫЙ!
- Упростить sqrt (–9) . Авторские права © Элизабет Стапель 2000-2011 Все права защищены
(Предупреждение: шаг, который проходит через третий знак «равно» — «», не «». i — это вне корня .)
TREE (3) и беспристрастные игры | Комплексное проективное 4-пространство
Изначально предполагалось, что эта статья будет о ДЕРЕВО (3) и функции занятого бобра. Однако я осознал потенциал превращения TREE (3) в конечную игру для двух игроков, что на удивление весело и означает, что в конечном итоге я оставил невычислимые функции на потом.
В прошлый раз мы исследовали быстрорастущую иерархию функций. Мы рассмотрели последовательность Гудштейна (или, скорее, эквивалентную задачу C8 ′), чтобы получить функцию, приблизительно равную f _ (ε_0), где ε_0 — довольно большой счетный порядковый номер. Рекурсивное применение этой конструкции соответствовало бы таким ординалам, как ε_0 + ω, которые не намного больше ε_0. Итак, если нам нужны более быстрые функции, нам нужны более мощные идеи.
ДЕРЕВО Фридмана (3)
Обычно мы ожидаем, что быстрорастущие функции будут иметь относительно плавный и устойчивый старт.Например, функция Аккермана начинается с {3, 4, 8, 65536, 2 ↑↑ (2 ↑↑ 65536),…}, а первые четыре члена довольно малы. Напротив, функция ДЕРЕВО начинается с ДЕРЕВО (1) = 1, ДЕРЕВО (2) = 3, а ДЕРЕВО (3) настолько огромно, невероятно велико, что намного превосходит все, что вы можете выразить в разумном объеме пространства с итерацией, рекурсией. и все остальное, упомянутое в предыдущем посте, включая C8 ′ и функцию Гудштейна.
Итак, что такое ДЕРЕВО? Определение довольно простое, если мы определим несколько терминов по ходу дела.Мы рассматриваем корневые деревья с k метками, которые представляют собой связанные ациклические графы, в которых одна вершина определяется как «корень», и каждая вершина может иметь один из k цветов. Пример показан ниже:
Существует бинарный оператор inf (не связанный с точной нижней гранью набора), который возвращает последнего общего предка двух вершин. Рассмотрим дерево выше. Если синяя вершина называется x , а зеленая вершина называется y , то x inf y = y .Точно так же inf двух некорневых красных вершин является корневой вершиной.
Мы говорим, что дерево S является гомеоморфно встраиваемым в дерево T , если существует инъекция φ из вершин S в вершины T , такая что:
- φ ( z ) и z имеют одинаковый цвет, для всех z в S ;
- φ ( x inf y ) = φ ( x ) inf φ ( y ), для всех x, y в S .
Эквивалентно это означает, что T является топологическим второстепенным по отношению к S (где мы направляем ребра относительно корневой вершины). Первое дерево гомеоморфно встраивается в это:
Доказательство: Удалите два зеленых листа, затем сократите двойной край, содержащий синюю вершину.
Если у нас есть бесконечная последовательность из k -помеченных деревьев { T _1, T _2, T _3,…}, где каждое T _ n имеет не более n вершин, тогда теорема Крускала о дереве утверждает, что некоторые T _ i могут быть гомеоморфно встроены в более поздние T _ j .Следовательно, в силу компактности существует некоторое значение ДЕРЕВО ( k ), которое представляет собой длину самой длинной возможной последовательности деревьев с метками k { T _1, T _2,…, T _TREE ( k )} такой, что | Т_н | ≤ n (для всех n) и никакое более раннее дерево не может быть гомеоморфно вложено в более позднее дерево.
Приведенная выше последовательность является самой длинной из таких последовательностей деревьев с двумя метками, поэтому ДЕРЕВО (2) = 3. Для любой последовательности первое дерево должно быть одной изолированной вершиной, и этот цвет не может встречаться в любом последующем дереве.Доказательство следует тривиально. Теперь рассмотрим 3-помеченные деревья. У нас может быть очень длинная последовательность, например, которая начинается так:
Как видите, к T _20 рисовать деревья становится сложно. Гораздо более эффективное обозначение — использовать сбалансированные круглые скобки:
T1 {}
T2 [[]]
T3 [() ()]
T4 [((()))]
T5 ([(())] [])
T6 ([(())] (()))
T7 ([(())] () () ())
T8 ([(())] () ())
T9 ([(())] ())
T10 ([(())])
T11 [(())]
T12 ([()] [()] [()] [()] [()] [])
T13 ([()] [()] [()] [()] [()] (()))
T14 ([()] [()] [()] [()] [()] () () ())
T15 ([()] [()] [()] [()] [()] () ())
T16 ([()] [()] [()] [()] [()] ())
T17 ([()] [()] [()] [()] [()])
T18 ([()] [()] [()] [()] [] [] [] [] [] [] [] [] [])
T19 ([()] [()] [()] [()] [] [] [] [] [] [] [] [] (()))
T20 ([()] [()] [()] [()] [] [] [] [] [] [] [] [] () () ())
T21 ([()] [()] [()] [()] [] [] [] [] [] [] [] [] () ())
T22 ([()] [()] [()] [()] [] [] [] [] [] [] [] [] ())
T23 ([()] [()] [()] [()] [] [] [] [] [] [] [] [])
... Родственная функция, tree , запрашивает самую длинную последовательность { U _1, U _2,…, U _tree ( r )} деревьев с меткой 1, таких что | У_н | ≤ n + r (для всех n ), и никакое дерево не может быть гомеоморфно вложено в более позднее дерево. Расширяя последовательность, показанную выше, можно доказать, что TREE (3) имеет следующую (слабую) нижнюю границу:
Доказательство (добавлено 24.07.2020 в ответ на неожиданно враждебные утверждения о том, что у меня никогда не было доказательства этой границы): После описанной выше последовательности можно создать новое дерево T24, которое имеет форму:
T24 ([()] [()] [()] [()] [] [] [] [] [] [] [] X7)
, где X7 — любое (одноцветно зеленое) дерево на 7 вершинах.После этого может идти последовательность:
T25 ([()] [()] [()] [()] [] [] [] [] [] [] [] X8) T26 ([()] [()] [()] [()] [] [] [] [] [] [] [] X9) T27 ([()] [()] [()] [()] [] [] [] [] [] [] [] X10) ...
, где X7, X8, X9, X10,… — последовательность максимальной длины для дерева (7). В конце этого процесса у нас есть:
T_ (23 + дерево (7)) ([()] [()] [()] [()] [] [] [] [] [] [] [] ())
as () обязательно является последним элементом последовательности максимальной длины для дерева (7). Затем мы можем расширить последовательность, «сжигая» еще один синий узел:
T_ (24 + дерево (7)) ([()] [()] [()] [()] [] [] [] [] [] [] []) T_ (25 + дерево (7)) ([()] [()] [()] [()] [] [] [] [] [] [] Y1)
, где Y1 — первое дерево в последовательности максимальной длины для дерева (дерево (7)).Мы действуем так же, как и раньше, с последовательностью членов дерева (дерево (7)), достигая высшей точки:
T_ (23 + дерево (7) + дерево (дерево (7))) ([()] [()] [()] [()] [] [] [] [] [] [] ()) T_ (24 + дерево (7) + дерево (дерево (7))) ([()] [()] [()] [()] [] [] [] [] [] []) T_ (25 + дерево (7) + дерево (дерево (7))) ([()] [()] [()] [()] [] [] [] [] [] Y2)
, где Y2 — первое дерево в последовательности максимальной длины для дерева (tree (tree (7))). 8 (7).8 (7)) (7). Повторение этой внешней итерации еще три раза приводит нас к заявленной границе.
Чтобы увидеть, что никакое дерево не встраивается гомеоморфно в более позднее дерево, отметим, что если T предшествует T ’, то мы имеем по крайней мере одно из следующего:
- T содержит больше копий [()], чем T ’;
- T содержит больше копий [], чем T ’;
- Монохроматическое зеленое поддерево T предшествует монохроматическому зеленому поддереву T ’;
, где последнее условие было обеспечено с помощью последовательности для дерева (k), которое имеет это свойство по определению.
Результат следует. QED
Игра Chomp
Чтобы быстро отвлечься от больших чисел, рассмотрим игру Chomp . Начнем с прямоугольной плитки шоколада размером м на n , нижний левый угол которой был пропитан цианидом.
Игроки ходят по очереди, съедая кусок шоколада вместе со всем, что сверху и справа от него. Например, после первого хода итоговая конфигурация может выглядеть так:
Затем второй игрок отвечает:
Так продолжается до тех пор, пока какой-нибудь неудачник не останется с залитым цианидом квадратом шоколада и не перенесет медленную, мучительную смерть.У кого есть выигрышная стратегия? Без явного построения стратегии выигрыша можно доказать, что первый игрок может добиться победы с помощью аргумента, известного как стратегия , кража .
Предположим, что у второго игрока есть выигрышная стратегия с намерением вывести противоречие. Пусть первый игрок (я обычно использую Габриэль и Вишал в качестве примеров имен в комбинаторной теории игр, а мы будем использовать алфавитный порядок, Габриэль) съест правый верхний квадрат шоколада:
Теперь у Вишала есть выигрышная стратегия.Предположим (без реальной потери общности), что он может добиться победы, сделав следующий ход:
Габриэль мог сделать этот ход с самого начала, поэтому у Вишала не может быть выигрышной стратегии. Reductio ad absurdum. Поскольку игра не может закончиться ничьей, мы заключаем, что у Габриэля есть выигрышная стратегия. Это доказательство в значительной степени неконструктивно, и никто не знает, какова эта выигрышная стратегия для произвольных натуральных чисел m, n .
Chomp называется беспристрастной игрой , поскольку те же ходы теоретически доступны каждому игроку, и это просто зависит от того, чей это ход. Ним — другой пример. Обе они могут быть выражены как poset games , в которых игроки по очереди удаляют любой элемент частично упорядоченного набора вместе со всеми более крупными элементами.
Создание игры из ДЕРЕВА (3)
Это было заслуженное отвлечение, но давайте вернемся к ДЕРЕВО (3). Мы можем определить беспристрастную игру для двух игроков (которая, кстати, является игрой по сетам) со следующими правилами:
- Игроки сменяют друг друга.
- На n -м ходу (нечетное для Габриэля, четное для Вишала) каждый игрок тянет дерево с тремя метками с не более чем n вершинами.
- Если вы нарисуете дерево так, что более раннее дерево гомеоморфно встраивается в него, вы проиграете.
По определению, такая игра длится не более ДЕРЕВА (3) ходов и никогда не может закончиться ничьей. Я не знаю, какова четность ДЕРЕВА (3), поэтому я не знаю, кто выиграет самую длинную игру. На самом деле, я даже не знаю, у какого игрока выигрышная стратегия в TREE (3), и исчерпывающий поиск непрактичен. [ Отредактировано 2020-08-21: , к сожалению, для первого игрока существует банальная выигрышная стратегия; после розыгрыша одной красной вершины реагируйте на каждый ход вашего оппонента, просто играя на последнем дереве оппонента, поменяв местами синий и зеленый цвета.Более интересна аналогичная игра на субкубических графах.]
Пример игры — это игра, в которой Вишал выигрывает после 8 ходов:
Хотите верьте, хотите нет, но все игры разумного размера Chomp могут происходить как позиции в естественных играх TREE (3). Для начала вернемся к предыдущей схеме получения действительно длинных последовательностей:
Теперь мы можем продолжать это очень долго ( x ходов, где x имеет эту невообразимо большую нижнюю границу):
После этой невероятно длинной последовательности ходов следующие шесть ходов могут быть следующими (пусть m и n будут положительными целыми числами, где m + n < x ; на практике x слишком велико что он неограничен):
Это может показаться не особенно плохим ходом со стороны Вишала, но выясняется, что теперь у Габриэля есть определенная выигрышная стратегия.Если игрок играет одну вершину (синюю или зеленую, так как красный был исчерпан на первом ходу), противник может выиграть, сыграв одну вершину другого цвета. Также обратите внимание, что ни у одного синего узла не может быть дочернего элемента, и ни одно дерево не может иметь глубину больше трех. Другими словами, последующие ходы выглядят так:
Этот конкретный ход сокращенно (4,3).
