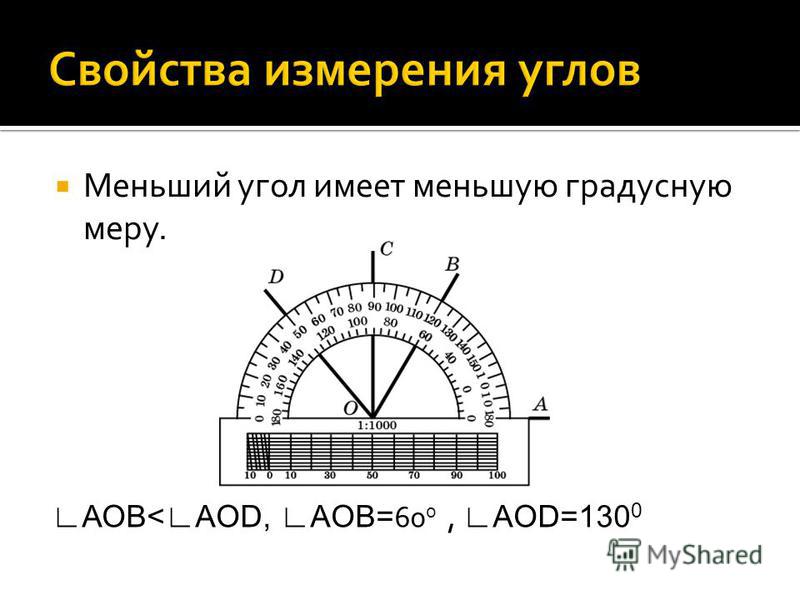
В каких единицах измеряют углы: §12. Виды углов. Измерение углов
§12. Виды углов. Измерение углов
ВОПРОСЫ1. Какой угол называют развернутым?
2. В каких единицах измеряют углы?
Углы измеряются в градусах.
3. Какова градусная мера развернутого угла?
Градусная мера развернутого угла равна 180º.
4. Что означает измерить угол?
Измерить угол — значит подсчитать, сколько единичных углов в нем помещается.
5. Как называется прибор, который используют для измерения углов?
Прибор, который используют для измерения углов, называется транспортир.
6. Расскажите как пользоваться транспортиром.
7. Какие градусные меры имеют равные углы?
Равные углы имеют равные градусные меры.
8. Какой из двух неравных углов считают большим?
Из двух неравных углов большим считается тот, градусная мера которого больше.
9. Каким свойством обладает величина угла?
10. Какой угол называют острым?
Острый угол — угол, градусная мера которого меньше 90º.
11. Какой угол называют прямым?
Прямой угол — угол, градусная мера которого равна 90º.
12. Какой угол называют тупым?
Тупой угол — угол, градусная мера которого больше 90º, но меньше 180º.
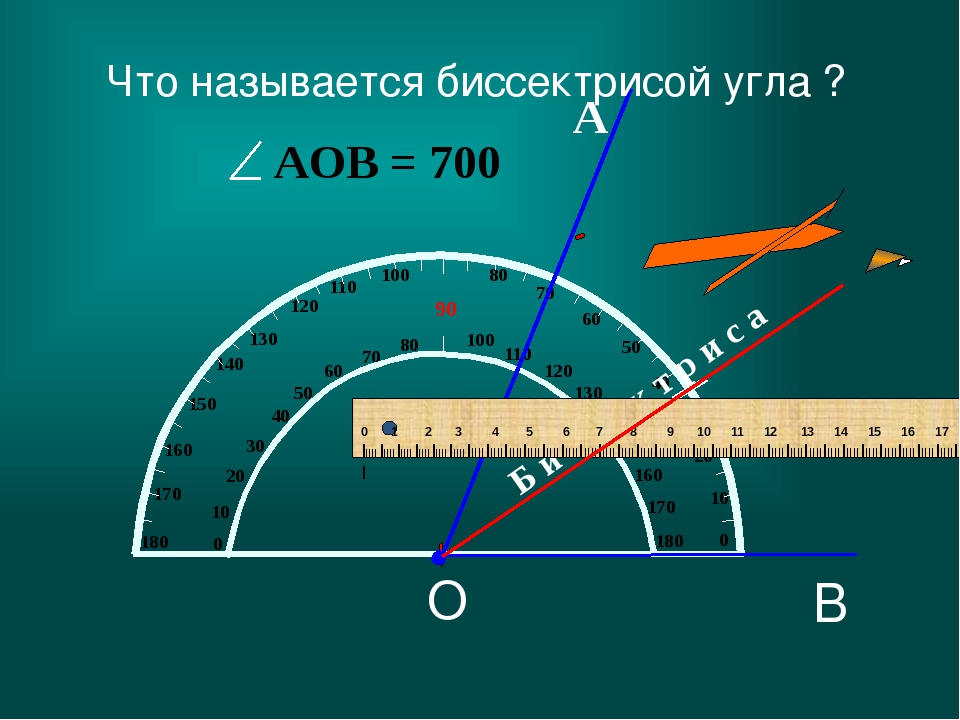
13. На какие углы делит развернутый угол его биссектриса?
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90º.
14. В каких случаях говорят, что от данного луча отложен данный угол?
РЕШАЕМ УСТНО
1. Назовите два числа, одно из которых: 1) на 27 больше другого; 3) в 7 раз меньше другого; 2) на 15 меньше другого; 4) в 3 раза больше другого.
2. Часы спешат на 10 мин и сейчас показывают время 10 ч 8 мин. Который час на самом деле?
Часы спешат на 10 мин и сейчас показывают время 10 ч 8 мин. Который час на самом деле?
На самом деле 9 ч 58 мин.
3. Часы отстают на 7 мин и сейчас показывают время 16 ч 55 мин. Который час на самом деле?
На самом деле 17 ч 2 мин.
5. Для озеленения улицы длиной 3 км на одной из ее сторон посадили деревья на расстоянии 20 м друг от друга. Сколько деревьев было посажено? Чему равно расстояние между первым и пятым деревьями?
УПРАЖНЕНИЯ
296. Начертите: 1) острый угол ЕFC; 2) прямой угол ОRT; 3) тупой угол D. 4) развернутый угол КАР.
297. Найдите на рисунке 93 острые, тупые и прямые углы.
298. Какие из данных углов острые, тупые, прямые, развернутые:
299. Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 94. Определите вид каждого угла.
Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 94. Определите вид каждого угла.
300. Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 95. Определите вид каждого угла.
301. Начертите угол, градусная мера которого равна: 1) 380; 2) 1240; 3) 920; 4) 900; 5) 870; 6) 540; 7) 1700; 8) 650. Определите вид каждого угла.
302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна: 1) 400; 2) 1300; 3) 680; 4) 1640. Определите вид каждого из построенных углов.
303. На рисунке 96 СМК = 1320, а угол АМК — развернутый. Вычислите величину угла АМС.
304. На рисунке 97 угол АОК — прямой, РОС = 540, а угол СОК — развернутый. Вычислите величину угла АОР.
305. Какой из углов, изображенных на рисунке 98, наибольший? Наименьший?
306. Начертите угол СDЕ, равный 1520. Лучом DА разделите этот угол на два угла так, чтобы СDА = 980. Вычислите величину угла АDE.
307. Начертите угол АВС, равный 1060. Лучом ВD разделите этот угол на два угла так, чтобы АВD = 340. Вычислите величину угла DВС.
308. Из вершины прямого угла ВОМ (рис. 99) проведены два луча ОА и ОС так, что ВОС = 740, АОМ = 620. Вычислите величину угла АОС.
309. Из вершины развернутого угла АСР (рис. 100) проведены два луча СТ и СF так, что АСF = 1580, ТСР = 1340. Вычислите величину угла ТСF.
310. Верно ли утверждение: 1) угол, который меньше тупого, — острый; 2) угол, который меньше развернутого, — тупой; 3) половина тупого угла — острый угол; 4) сумма градусных мер двух острых углов больше 900; 5) угол, который больше прямого, — тупой.
311. Найдите градусную меру угла между стрелками часов, если они показывают: 1) 3 ч; 2) 6 ч; 3) 4 ч; 4) 11 ч; 5) 7 ч.
312. Луч ВК является биссектрисой угла СВD, АВК = 1460 (рис. 101, ). Вычислите градусную меру угла СВD.
313. Луч ОА является биссектрисой угла СОМ, СОМ = 540 (рис. 101, б). Вычислите градусную меру угла ВОА.
314. Проведите три прямые, пересекающиеся в одной точке. Запишите все развернутые углы, образовавшиеся при этом.
315. Проведите шесть прямых, пересекающихся в одной точке. Верно ли, что среди образовавшихся при этом углов есть угол, градусная мера которого меньше 310?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
316. Заполните цепочку вычислений:
317. Верно ли неравенство (а + 253)7(9 864 — а) : 4 при а= 124?
Верно ли неравенство (а + 253)7(9 864 — а) : 4 при а= 124?
318. В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько граммов молока помещается в стакан?
319. Длина границы России с Китаем, Монголией и Казахстаном составляет 15 293 км. Найдите длину границы России с каждым из этих государств, если длина границы с Китаем и Монголией равна 7 694 км, а с Китаем и Казахстаном — 11 808 км.
ЗАДАЧА ОТ МУДРОЙ СОВЫ
320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает по нему на 2 м вниз. На какой день она доберется до вершины столба, высота которого равна 20 м?
Как и чем измеряются углы.
Методы и средства контроля и измерения углов
Углы и измерение углов
Угловые размеры определяют положение плоскостей, осей, линий, центров отверстий и т. д. Угловые размеры бывают зависимые и назависимые.
д. Угловые размеры бывают зависимые и назависимые.
Независимые углы не связаны с другими параметрами изделия; зависимые углы определяются основными параметрами изделий, к которым они относятся.
В качестве единицы измерения плоских углов Международной системой единиц (СИ) принят радиан — угол между двумя радиусами круга, вырезающими на его окружности дугу, длина которой равна радиусу данного круга.
По этой причине в машиностроении для угловых измерений в основном применяются внесистемные единицы: градус, минута и секунда. Эти единицы связаны между собой следующими соотношениями:
- 1 рад = 57°17׳45״ = 206 265″
- 1° = π/180 рад = 1,745329 × 10-2 рад;
- 1‘ = π /10800 рад = 2,908882 × 10-1 рад;
- 1” = π/648000 рад = 4,848137 × 10-6 рад.

Значение угла при измерении определяют сравнением его с известным углом. Известный угол может быть задан так называемыми жесткими (с постоянным значением угла) мерами — аналогами формы элементов детали: угловыми мерами, угольниками, угловыми шаблонами, коническими калибрами, многогранными призмами.
Измеряемый угол можно сравнивать также с многозначными угломерными штриховыми мерами и различными видами круговых и секторных шкал. Еще одним методом получения известного угла является его расчет по значениям линейных размеров на основании тригонометрических зависимостей.
В соответствии с этим классификацию методов измерений углов производят в первую очередь по виду создания известного угла: сравнением с жесткой мерой, сравнением с штриховой мерой (гониометрические методы) и тригонометрическими методами (по значениям линейных размеров).
При сравнении углов с жесткой мерой отклонение измеряемого угла от угла меры определяют по просвету между соответствующими сторонами углов детали и меры, по отклонению показаний прибора линейных размеров, измеряющих несовпадение этих сторон или при контроле «по краске», т. е. по характеру тонкого, слоя краски, перенесенного с одной поверхности на другую.
е. по характеру тонкого, слоя краски, перенесенного с одной поверхности на другую.
В приборах для гониометрических измерений имеются штриховая угломерная шкала, указатель и устройство для определения положения сторон угла. Это устройство связано с указателем или шкалой, а измеряемая деталь — соответственно со шкалой или указателем. Определение положения сторон угла можно производить как контактным, так и бесконтактным (оптическим) способом. При соответствующих измеряемому углу положениях узлов прибора определяют угол относительного поворота шкалы и указателя.
При косвенных тригонометрических методах определяют линейные размеры сторон прямоугольного треугольника, соответствующего измеряемому углу, и по ним находят синус или тангенс этого угла (координатные измерения). В других случаях (измерение с помощью синусных или тангенсных линеек) воспроизводят прямоугольный треугольник с углом, номинально равным измеряемому, и устанавливая его как накрест лежащий с измеряемым углом, определяют линейные отклонения от параллельности стороны измеряемого угла основанию прямоугольного треугольника.
При всех методах измерений углов должно быть обеспечено измерение угла в плоскости, перпендикулярной к ребру двугранного угла. Перекосы приводят к погрешности измерения.
При наличии наклона плоскости измерения в двух направлениях погрешность измерения угла может быть и положительной и отрицательной. При измерениях малых углов эта погрешность не превысит 1% значения угла при углах наклона плоскости измерения до 8°. Такая же зависимость погрешности измерения угла от углов перекоса получается и в случаях неточного базирования деталей на синусной линейке, несовпадения направления ребра измеряемого угла или оси призмы с осью поворота на гониометрических приборах (при фиксации положения граней по автоколлиматору), при измерениях с помощью уровней и т.п.
Угол наклона плоскостей обычно определяется уклоном, численно равным тангенсу угла наклона.
Малые значения уклонов часто указывают в микрометрах на 100 мм длины, в промилле или миллиметрах на метр длины (мм/м).
Например, в мм/м указывается цена деления уровней. Пересчет уклонов в угол обычно производится по приближенной зависимости: уклон 0,01 мм/м (или 1 мкм/100 мм) соответствует углу наклона в 2″ (погрешность подсчета угла по этой зависимости составляет — 3%).
Как было показано выше в машиностроении в зависимости от используемых средств и методов различают три основных способа измерения углов:
Сравнительный метод измерения углов с помощью жестких угловых мер. При этом измерении определяется отклонение измеряемого угла от угла меры.
Абсолютный гониометрический метод измерения углов, при котором измеряемый угол определяется непосредственно по угломерной шкале прибора.
Косвенный тригонометрический метод: угол определяется расчетным путем по результатам измерения линейных размеров (катетов, гипотенузы), связанных с измеряемым углом тригонометрической функцией (синусом или тангенсом).
Сравнительный метод измерения углов обычно сочетается с косвенным тригонометрическим методом, последним определяется разница сравниваемых углов в линейных величинах на определенной длине стороны угла.
***
Угловые призматические меры и угольники
Угловые призматические меры служат для хранения и передачи единицы плоского угла. Их применяют для проверки шаблонов и угловых размеров различных изделий; для градиуровки угломерных приборов, а также для непосредственных измерений.
Угловые меры, предназначенные для проверки угломерных приборов и рабочих мер, называют образцовыми.
По точности аттестации образцовые угловые меры делят на четыре разряда (1,2,3 и 4). Предельные погрешности аттестации рабочих углов не должны превышать для угловых мер 1-го разряда — ±0,5”; 2-го разряда — ±1”; 3-го — ±3”; 4-го — ±6”.
Угловые меры собирают в блоки с помощью специальных державок.
Контроль углов угольниками осуществляют, оценивая просвет между угольником и контролируемой деталью на глаз, или сравнивают с образцовой щелью, созданной с помощью концевых мер длины и лекальной линейки.
При использовании крупных угольников просвет оценивают с помощью щупов.
Погрешность проверки углов угольником зависит от погрешности самого угольника, длины сторон угла, по которой производится проверка, и других факторов.
Угломеры с нониусами
Угломеры с нониусами применяют для измерения профиля угла на деталях контактным методом с отсчетом по угловому нониусу с точностью 2‘ и 5‘. Состоит угломер из круглого угломерного диска, скрепленного с корпусом зажимной гайкой. На основании смонтированы установочная планка и нониус с нанесенными 30 делениями с двух сторон от нулевого штриха; каждое деление соответствует 2 мин.
Линейка с лицевой стороны имеет продольный ласточкообразный паз, по которому перемешается (в процессе установки линейки на угол) хвостовик прижима.
При измерении угломер накладывают на проверяемую плоскость детали так, чтобы линейка и рабочая плоскость корпуса были совмещены со сторонами измеряемого угла.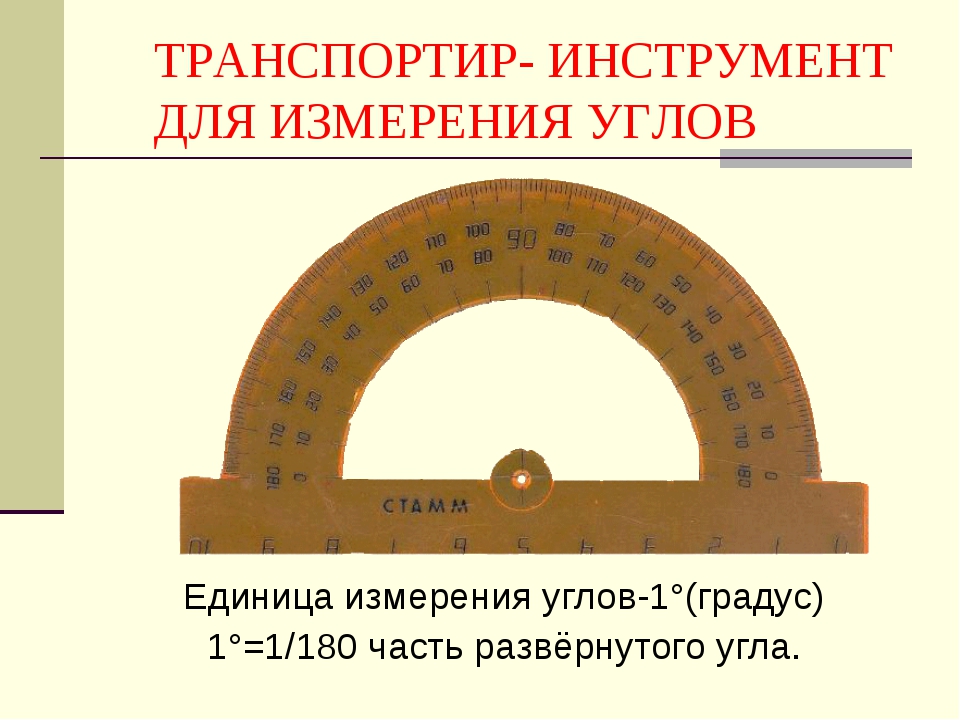 Целое число градусов отсчитывают по шкале диска до нулевого деления (штриха) нониуса. Затем определяют деление нониуса, совпадающего с делениями основной шкалы (диска).
Целое число градусов отсчитывают по шкале диска до нулевого деления (штриха) нониуса. Затем определяют деление нониуса, совпадающего с делениями основной шкалы (диска).
После этого определяют по нониусу сколько минут и градусов совпадают с делениями нониуса.
Оптический угломер
В корпусе оптического угломера закреплен стеклянный диск со шкалой, имеющей деления в градусах и минутах. Цена малых делений 10 ‘. С корпусом жестко скреплена основная (неподвижная) линейка. На диске смонтированы лупа, рычаг и укреплена подвижная линейка.
Под лупой параллельно стеклянному диску расположена небольшая стеклянная пластинка, на которой нанесен указатель, ясно видимый через окуляр. Линейку можно перемещать в продольном направлении и с помощью рычага закреплять в нужном положении.
Во время поворота линейки в ту или другую сторону будет вращаться в том же направлении диск и лупа. Таким образом, определенному положению линейки будет соответствовать вполне определенное положение диска и лупы. После закрепления линеек зажимным кольцом через лупу отсчитывают показания угломера.
После закрепления линеек зажимным кольцом через лупу отсчитывают показания угломера.
Оптическим угломером можно измерять углы от 0 до 180°. Допускаемые погрешности показания оптического угломера ±5‘.
Индикаторный угломер
В индикаторном угломере обычная шкала и нониус заменены индикаторным циферблатом. Отсчет угловых размеров производится по показаниям стрелки на большой шкале через 10°. Цена деления 5‘, предел измерения угломера 0…360°.
Портативный оптический угломер-шаблон
Портативный оптический угломер-шаблон предназначен для проверки профиля резцов. Он состоит из стандартной восьмикратной лупы, неподвижно закрепленной на прозрачном диске из органического стекла. Вокруг оси, запрессованной в этот диск, свободно поворачивается стальной диск, по периметру которого с высокой точностью выполнены шаблоны наиболее часто встречающихся в практике углов, радиусов и кривых. Нужный профиль шаблона накладывают на затачиваемый резец и под лупой проверяют точность доводки.
Прибор отличается точностью и удобством, так как им можно пользоваться непосредственно на рабочем месте.
***
Допуски и посадки конических соединений
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Зачем нужен конвертер длины, в каких единицах измеряют длину
С самого начала человечества была необходимость измерять длину или расстояние. Для этого использовались наиболее простые и доступные средства, как правило, это были части тела. В разных странах использовались различные системы, поэтому появились свои определения этой величины. В системе СИ основной единицей измерения физической длины являются метры. Поскольку сегодня на равных правах используют несколько мер длины, то часто возникает необходимость их перевода. Чтобы не искать дополнительные параметры и соотношения, рекомендуем использовать Онлайн конвертер длины.
Как использовать конвертер длины
В нашем конвертере собраны самые популярные системы измерения длины:
- Метрическая — это десятичные числа, кратные метру (метр, километр, дециметр, сантиметр, миллиметр, микрометр, нанометр, ангстрем и т. д).
- Британо-американская — миля, ярд, фут, дюйм.
- Старорусская — верста, сажень, аршин, локоть и др.
- Морская — морская миля, лье, кабельтов Великобритания, США).
- Астрономические единицы — парсек, световой год.
- Типографские единицы — пункт, пиксель.
Чтобы сделать перевод из одной системы длины в другую введите число в поле и выберите саму систему. Для ввода дроби можно использовать точку ( . ) Или запятую ( , ). В следующем поле выберите опцию, в которой надо пересчитать. Нажмите кнопку “Перевести”.
Единицы длины, которые часто используют, как в математике, так и в физике:
| 1 километр (км) | 1000 метров (м) |
| 1 метр (м) | 100 сантиметров (см) |
| 1 дециметр (дм) | 10 сантиметров (см) |
| 1 метр (м) | 1000 миллиметров (мм) |
| 1 сантиметр (см) | 10 миллиметров (мм) |
В Англии и Америке пользуются другими единицами, хотя они не занесены в систему СИ, все равно очень популярны:
| 1 дюйм (inch) | 2,54 сантиметра (см) |
| 1 фут (foot) | 30,48 сантиметра (см) или 12 дюймов |
| 1 ярд (yard) | 91,44 см или 3 фута |
| 1 миля (mile) | 1609,344 метра (м) или 1760 ярдов |
| 1 морская миля (Mn) | 1852 метра (м) или 2025,372 ярда |
В астрономии используют специальные единицы для определения расстояний:
- астрономическая единица (au) = 149597870700 метров (m)
- 1 световой год = 9,4607 x 1015 метров = 63 241 астрономическая единица (au)
- парсек = 30,8568 трлн км
Что такое длина и как ее измерить
Длина — это физическая мера расстояния между двумя точками в пространстве. Она измеряется в соответствии с евклидовой метрикой (классический метод измерения расстояний) и, как правило, обозначается буквой L. Она может быть измерена
Она измеряется в соответствии с евклидовой метрикой (классический метод измерения расстояний) и, как правило, обозначается буквой L. Она может быть измерена
по прямой линии (например, длина волны, расстояние между полом и потолком),
по кривой (например, длина пути, пройденного объектом).
Базовая единица измерения длины (согласно системе СИ) — это метр. Точное определение метра было принято на 17-ой Генеральной конференции мер и весов в 1983 году. 1 м — это расстояние, которое свет проходит в вакууме за время 1/299 792 458 с.
Длина никогда не может принимать отрицательные значения.
Для измерения длины используются такие устройства, как:
- лазерные линейки (измерение очень больших расстояний),
- строительные линейки (размером до нескольких метров),
- штангенциркуль (для измерения небольших расстояний в несколько миллиметров),
- а также линейка или рулетка.
Для преобразования в разные системы используют конвертер длины
Меры длины. Несколько фактов из истории
Несколько фактов из истории
Самыми древними единицами измерения длины, которые люди использовали чаще всего, были части тела (локоть, палец, ступня, шаг и т.д.).
В Древнем Египте это были локти, руки или пальцы.
- Локоть — это расстояние от сгиба локтя до кончика среднего пальца, он равнялся длине семи рук.
- Одна рука — равнялась ширине четырех пальцев.
Древние римляне измеряли расстояния ступнями (foot- фут). Более короткие участки меряли шириной большого пальца. Для определения длины больших размеров использовали шаги.
Тысяча шагов римского солдата была милей
Торговцы текстилем установили единицу измерения, известную как ярд — это длина от подбородка до кончиков пальцев вытянутой руки. Придерживая материал подбородком, они вытягивали руку, таким образом измеряя длину отреза.
Еще есть версия что ярд ввел в обиход король Англии Эдгар и он равнялся расстоянию от кончика его носа до среднего пальца вытянутой руки. Поскольку короли менялись и их телосложение с
Поскольку короли менялись и их телосложение с
Урок 11: Единицы измерения — 100urokov.ru
План урока:
Луч, угол, отрезок
Измерение отрезков. Сантиметр. Дециметр
Геометрические фигуры. Треугольник. Четырехугольник. Многоугольники
Килограмм
Литр
Начинаем наш урок
Пусть тебе пойдет он впрок.
Будем вместе рассуждать,
Наблюдать и измерять.
Наверное, каждый ребенок мечтает быть изобретателем или исследователем. Надеюсь, ты тоже, ведь наш урок мы проведем в лаборатории.
Там мы будем моделировать, проводить разные опыты и измерения. Ты узнаешь много нового, познакомишься с различными измерительными инструментами. Я научу тебя как нужно ими пользоваться. Итак, приступим.
Луч, угол, отрезок
Давай вспомним материал из нашего первого урока. Мы знакомились с некоторыми геометрическими понятиями и выучили названия основных геометрических фигур. Посмотри на картинку и попробуй назвать, что здесь изображено.
Посмотри на картинку и попробуй назвать, что здесь изображено.
Проверь, все ли ты правильно вспомнил.
Замечательно. А теперь мы приступим к изучению нового. Начнем с самого простого.
Это луч.
Как ты думаешь, почему его так называют?
Если присмотреться, то мы можем представить, что точка – это солнышко. Оно испускает лучи.
Обрати внимание, что все лучи исходят из центра солнца. У них общее начало.
Мы возьмем только два луча, которые исходят из одной точки.
Теперь давай поэкспериментируем. Сделаем модель угла. Нужно две палочки. Это могут быть счетные палочки, палочки для мороженого или обычные зубочистки.
Теперь поучимся чертить угол в тетради. Для этого нам понадобится линейка и карандаш.
Нужно положить линейку на лист и крепко прижать ее левой рукой. Поставь карандаш возле ее верхнего края.
У нас получился отрезок. Это часть прямой, которая с двух сторон ограничена точками. Значит, у отрезка должно быть две точки.
Значит, у отрезка должно быть две точки.
Создадим модель отрезка. Сделай два шарика из пластилина и прикрепи их с обеих сторон палочки.
Готово. Правда, это было легко?
Чертить отрезок в тетради тоже не сложно. Действуем так же, как и при черчении луча.
После того как проведем под линейку прямую линию, отметим точками начало и конец отрезка.
Длина отрезка может быть разной. Его можно начертить совсем маленьким или продлить на всю страничку и даже выйти за нее. Потренируйся чертить разные отрезки в разном направлении.
Скажи, ты можешь определить, какой отрезок больше? Какой самый маленький? Есть ли здесь равные отрезки? На сколько один отрезок больше, чем другой? Как начертить отрезок, который будет заданной длины?
На все эти вопросы мы ответим после работы в нашей лаборатории.
Измерение отрезков. Сантиметр. Дециметр
Чтобы сравнивать, нам нужно научиться измерять отрезки. Это можно делать и с помощью обычной палочки. Найди себе подходящую палочку, и мы вместе проведем измерения.
Это можно делать и с помощью обычной палочки. Найди себе подходящую палочку, и мы вместе проведем измерения.
Следует приложить ее начало к началу отрезка и отметить на палочке конец отрезка.
Теперь эту же палочку приложим к другому отрезку, тоже соединив их начало. И отметим конец этого отрезка.
Мы получили на палочке две отметки. Чья отметка находится дальше, тот отрезок и больше по длине.
Мы можем с помощью этой палочки чертить равные отрезки. Нужно только приложить ее к листу тетради и провести вдоль нее линию от начала и до нужной отметки.
Попробовал? Мы получили точно такой же отрезок, как и тот, что измеряли первым и отметили его длину красной черточкой.
Однако, измеряя отрезки палочкой мы получаем о них очень мало информации, которую нельзя никому передать или записать. Например, как ты расскажешь своему другу о своих измерениях в нашей лаборатории? Какой длины оказались твои отрезки? Кусочек палочки?
Это похоже на то, как герои мультфильма пытались измерить длину удава, считая ее шагами, попугаями и даже мартышками.
Но мы с тобой занимаемся научными исследованиями, а значит, все измерения должны быть точными и правильно записанными. Поэтому сейчас познакомимся с инструментами и единицами измерения, необходимыми для определения длины отрезков.
Ты уже знаком с линейкой. Возьми ее и положи перед собой.
Мы ее использовали для проведения прямых линий. Но линейка является измерительным инструментом. Рассмотри ее. На ней нанесены штрихи и цифры. Обрати внимание, что штрихи разной длины, а цифры написаны только возле самых длинных черточек.
Это шкала измерений. Начало отсчета обозначено числом 0, а дальше идут числа по порядку, как в числовом ряду, который тебе уже знаком.
Особенность шкалы заключается в том, что расстояние между схожими штрихами одинаковое. Сегодня мы будем изучать только длинные черточки. Часть шкалы от одной длинной черточки до соседней длинной черточки называется сантиметр. Отметим на рисунке 1 сантиметр.
Сантиметр – это единица измерения длины отрезков. Вся шкала на линейке разделена на сантиметры.
Вся шкала на линейке разделена на сантиметры.
Давай посчитаем каждый сантиметр на линейке. Например, здесь мы отметили пять сантиметров и остановились на числе 5.
Числа указывают сколько сантиметров отсчитано от числа 0. Поэтому мы, начиная измерять или чертить отрезок, обязательно совмещаем его начало с черточкой возле числа 0.
Например, выполним измерение отрезка. Приставим к точке, которая отмечает начало отрезка, черточку возле числа 0. Линейку нужно положить ровно вдоль линии.
После такого совмещения посмотрим на точку, которая отмечает конец отрезка. Она находится возле черточки, внизу которой написано число 7. Значит длина этого отрезка составляет 7 сантиметров.
Все довольно просто. Главное – соблюдать точность.
Чтобы записать длину отрезка будем использовать короткую запись см. Пишем так:
7 см
Сейчас мы используем полученные навыки для проведения опыта. Нам нужно найти равные отрезки.
Нам нужно найти равные отрезки.
Глядя на отрезки, нельзя сразу сказать, какие из них одинаковые. Чтобы найти равные отрезки, нужно провести их измерения. Посмотри, как мы это сделали.
Определи размеры каждого отрезка в сантиметрах.
Я тоже это сделала. У меня получилось так.
Итак, мы опытным путем установили, что здесь два одинаковых отрезка, длина которых 12 см.
Никаких сомнений быть не может – все точно.
Потренируйся проводить самостоятельные измерения. Попроси кого-то из взрослых начертить тебе несколько отрезков, а ты измерь их длину.
А сейчас ты и сам научишься чертить отрезки. Это тоже легко. Например, начертим отрезок длиной 4 см.
Приложим линейку. Поставим точку напротив числа 0.
Не сдвигая линейку, поставим точку напротив числа, соответствующего длине отрезка. В нашем случае это число 4.
Теперь крепко прижмем линейку. Убедимся, что обе точки находятся непосредственно у верхнего края линейки. Поставим карандаш на первую точку и плавно проведем линию до второй точки.
Убедимся, что обе точки находятся непосредственно у верхнего края линейки. Поставим карандаш на первую точку и плавно проведем линию до второй точки.
Теперь линейку можно убирать. Отрезок готов.
Теперь твоя очередь. Выполни аналогичные действия в такой же последовательности, чтобы начертить отрезок длиной 6 см.
А теперь взгляни на рисунок и скажи, сколько сантиметров составляет длина этого отрезка.
Итак, мы установили, что длину отрезка можно записать, как 13 см, а можно, как 1 дм 3 см. Это можно делать с любым отрезком, если его длина выражена двузначным числом. Подумай, как можно еще записать длину отрезка, если мы определили, что она составляет 17 см.
Правильно, это будет 1 дм 7 см.
Замечательно. Ты усвоил много новой информации об угле, отрезке и единицах измерения длины. Дальше будет проще, потому что основное ты уже знаешь.
Геометрические фигуры. Треугольник. Четырехугольник. Многоугольники
Давай вернемся к нашей модели угла.
Такие замкнутые ломаные линии являются геометрическими фигурами. Мы уже с тобой посчитали, что в этой фигуре три угла. Каждый угол имеет вершину – точку, в которой соединяются две стороны угла. Значит вершин тоже три. А теперь посчитай, сколько палочек мы использовали.
И палочек тоже три, т.е. у фигуры три стороны.
Такая фигура называется треугольник. Ты уже знаешь это название и знаешь, как выглядит треугольник. Сегодня мы выучили основные характеристики этой фигуры. Треугольники бывают разные и по размеру, и по виду.
Главное, что у треугольника три угла, три вершины и три стороны. Наверное, и название у него такое, потому что у него всего по три.
Вокруг нас есть много предметов, которые имеют треугольную форму. Например, крыши домов.
Убедись, что это треугольник – посчитай стороны крыши. Их три, значит, красная фигура является треугольником.
Вспомни, что еще похоже на треугольник.
А сейчас давай продолжим моделировать. Разъедини две палочки и сделай их все отрезками.
Посчитай углы каждого четырехугольника.
Убедился? Любая фигура, у которой есть четыре угла, является четырехугольником. Мы знаем очень много предметов, которые имеют четырехугольную форму. Например, тетрадь и книга.
Все эти предметы имеют по четыре стороны, а значит они четырехугольники.
Надеюсь, ты уже понял связь между названием и строением фигуры. Подумай, какую фигуру называют пятиугольником?
Правильно, это фигура, у которой пять углов, пять вершин и пять сторон. Знаешь, как его смоделировать?
Сначала разъединим любые две палочки.
Посчитай углы и стороны каждого многоугольника и назови их. Найди среди этих фигур четырехугольники.
Обрати внимание, что сторонами фигур являются отрезки. Значит, их можно измерять. Для этого нужна линейка. Ты уже знаешь, как ею пользоваться.
Давай измерим каждую сторону треугольника.
Длина третей стороны 13 см. Это тоже можно записать в другом виде: 1 дм 3 см.
Мы отлично справились. Наша работа не прошла в пустую. Теперь ты можешь правильно назвать почти любую геометрическую фигуру.А с помощью линейки сумеешь измерить стороны у любой фигуры.
Килограмм
Продолжим. Будем снова измерять. Только уже совсем по-другому. Нам нужно сравнить два предмета.
Что ты можешь сказать? Чем они отличаются?
Конечно, они отличаются по цвету, но ведь мы изучаем математические понятия. Поэтому поговорим о других параметрах.
Ты уже, наверное, догадался, о чем речь. Арбуз тяжелый, а мяч легкий. Это значит, что у них разная масса. Итак, мы поговорим о том, что у предметов можно измерять массу, т.е. узнавать, сколько они весят. Какой измерительный инструмент нам нужен для определения массы?
Какой измерительный инструмент нам нужен для определения массы?
Это весы. Они бывают разных видов.
Есть весы с чашами. Они называются механическими.
На одну чашу нужно положить сам предмет, а на другую чашу ставят гири. Следует подобрать такие гири, чтобы чаши весов оказались на одном уровне.
А сколько весит арбуз? Определи общее количество килограммов на гирях.
Правильно, 5 и 2 будет 7. Значит, арбуз весит 7 кг.
Все очень просто и интересно. Попроси родителей купить себе такой набор и потренируйся взвешивать разные предметы, которые есть в твоей комнате.
Запомни, что их масса измеряется в килограммах.
Литр
А теперь нам нужно измерить молоко. Как мы будем наливать его на чашу весов? Что произойдет?
Верно, если лить молоко, то оно разольется по столу и ничего измерить не получится. Молоко нужно лить в посуду: бутылку, стакан, банку.
Как же измерить, сколько молока вместилось в бидон или кувшин? Для этого есть еще одна единица измерения – литр. Она нужна для измерения вместимости. При этом используется специальная мерная посуда, на которой нанесена шкала.
Она нужна для измерения вместимости. При этом используется специальная мерная посуда, на которой нанесена шкала.
Чтобы определить, сколько литров молока находится в кувшине, надо перелить его в мерную посуду и посмотреть какой метки достигнет его уровень.Таким образом, мы можем измерить не только количество молока, но и любой другой жидкости.
Есть емкости, которые имеют определенный объем. Например, вот посуда, которая вмещает 1 литр.
Записывается так:
1 литр – 1 л
Вот мы и закончили наш урок. Ты узнал много нового. Теперь ты знаешь, как начертить многоугольник.
А главное, мы выучили единицы измерения. Вот что ты должен запомнить.
Сегодня мы сделали только первый шаг в деле исследования. Надеюсь, тебе понравилось проводить опыты, моделировать и ты продолжишь это делать самостоятельно.А сейчас выполни несколько проверочных заданий.
градусов как единица измерения угла
градус как единица измерения угла — Math Open Reference Определение: мера угол. Один градус — это одна 360-я часть полного круга.
Один градус — это одна 360-я часть полного круга.Попробуй это Отрегулируйте угол ниже, перетащив оранжевый на R. Обратите внимание на количество градусов для любого конкретного угла.
Измерение угла
В геометрии угол. измеряется в градусах, где полный круг равен 360 градусам. Небольшой угол может составлять около 30 градусов.Обычно, когда требуется более точная мера, мы просто добавляем десятичные знаки к градусам. Например 45,12 °
Маленький кружок после числа означает «градусы». Таким образом, это будет произноситься как «сорок пять целых два десятых градуса».
градуса — минуты — секунды
При измерении широты и долготы каждый градус делится на минуты и секунды.
Степень делится на 60 минут. Для более точных измерений минута снова делится на 60 секунд,
Однако эта последняя мера настолько мала, что используется только там, где углы
поданный
на экстремальных расстояниях, таких как астрономические измерения и измерения широты и долготы.
Эти минуты и секунды (как ни странно) не имеют ничего общего со временем. Они просто все меньшие и меньшие части градуса.
См. Также Градусы — Минуты — Калькулятор секунд. для калькулятора, который может складывать и вычитать углы в этой форме.
| Установка | письменный | Заявлено |
| Градусов | С маленьким кружком после номера. Пример 61 ° | «61 градус» |
| Минуты | С небольшим тире после номера. Пример 34 ° 21 ‘ | «34 градуса, 21 минута» |
| Секунды | С двумя маленькими черточками. Пример 32 ° 34 ’44’ | «32 градуса, 34 минуты, 44 секунды» |

В каком направлении измерять?
На рисунке выше отрегулируйте точку R так, чтобы линия пересекала точку с отметкой 315 °.Начиная с Q и идя против часовой стрелки, мы видим, что размер равен 315 °. Но если бы мы пошли по часовой стрелке от Q, это было бы 45 ° (360-315). Что правильно?
Они оба, но по соглашению предполагается меньший. Поэтому в этих условиях угол в центре составляет 45 °. Большая мера (315 °) называется угол рефлекса RPQ.
Углы, которые вы должны знать
Используйте рисунок выше, чтобы узнать, как выглядят различные угловые меры, измеренные в градусах.В общем, вы должны уметь чтобы визуально оценить любой угол с точностью до 15 °, и вы должны быть в состоянии распознать общие углы (показаны красным) на виду и сами зарисовать их.Прочие меры
Радианы
Угол может быть измерен в радианах, где полный круг равен 2 пи радиана (около 6,28). Это широко используется в тригонометрии.Грады
В некоторых маркшейдерских работах используется град. В круге 400 градусов, значит, прямой угол равен 100 градусам.Вы редко увидите этот агрегат. Думайте об оценках как о «метрических градусах».
В круге 400 градусов, значит, прямой угол равен 100 градусам.Вы редко увидите этот агрегат. Думайте об оценках как о «метрических градусах».Морские углы
Судовые навигаторы используют углы, которые измеряются несколько иначе, с помощью системы, разработанной сотни лет назад для Nautical Alamanac — книги навигационных таблиц. Каждый градус как обычно делится на 60 минут, но секунд нет. Вместо этого минута выражается в десятичном формате. Например, 23 ° 34,62 ‘читается как «23 градуса 34,62 минуты. См. Также «Калькулятор морского угла».
Что попробовать
- На рисунке выше нажмите «Скрыть детали».
- Отрегулируйте положение точки R
- Оценить угол RPQ
- Нажмите «Показать подробности», чтобы узнать, насколько близко вы
- Повтор.
Вы должны быть особенно в состоянии оценить углы, близкие к красным на рисунке выше, поскольку они часто встречаются в геометрии.
Другие ракурсы
Общие
Угловые типы
Угловые отношения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Измерительные углы
Угол образуется, когда два отрезка или луча (стороны угла угла) встречаются в общей конечной точке (вершина ). Фактически образуется два угла. Обычно один из этих углов будет меньше ста восьмидесяти градусов (т.е. это будет острый угол , прямой угол или тупой угол ), а другой угол будет больше ста и восемьдесят градусов (т.е. угол рефлекс ). Иногда оба угла будут равны прямым углам (то есть они оба будут равны ровно сто восемьдесят градусов). Если вам нужен более подробный взгляд на углы в целом, может быть полезно прочитать страницу под названием «Углы» в разделе Geometry . Тригонометрия в первую очередь связана с измерением углов.
Конечно, мы можем достаточно легко измерить углы, нарисованные на бумаге, с помощью транспортира, хотя точность измерения зависит как от навыков человека, измеряющего угол, так и от того, насколько точен рисунок в начале. Однако есть много ситуаций, когда мы не можем использовать простое устройство, такое как транспортир, для измерения угла. Вместо этого мы должны получить значение угла путем расчетов на основе доступной информации. Тригонометрия предоставляет ряд функций, которые позволяют нам производить вычисления с использованием углов. Тригонометрическая функция (или функции), используемая для конкретной ситуации, будет зависеть от того, какая информация у нас есть, и какие значения мы пытаемся найти.
Однако есть много ситуаций, когда мы не можем использовать простое устройство, такое как транспортир, для измерения угла. Вместо этого мы должны получить значение угла путем расчетов на основе доступной информации. Тригонометрия предоставляет ряд функций, которые позволяют нам производить вычисления с использованием углов. Тригонометрическая функция (или функции), используемая для конкретной ситуации, будет зависеть от того, какая информация у нас есть, и какие значения мы пытаемся найти.
Размер угла определяется тем, насколько одну из сторон нужно повернуть вокруг вершины, чтобы она лежала прямо над другой стороной.Величина необходимого поворота обычно измеряется либо в градусах , либо в радианах . Один градусов дуги (чтобы дать ему полное название) представляет собой поворот на на одну триста шестидесятую ( 1 / 360 ) полного кругового вращения. Градус может быть дополнительно разделен на шестьдесят равных интервалов, называемых угловых минут (или просто минут ), и каждая угловая минута также может быть разделена на шестьдесят равных интервалов, называемых угловых секунд (или просто секунд ). В настоящее время существует тенденция использовать десятичное представление для дробной части градуса, но иногда все еще используются минуты и секунды. Следующие значения углов эквивалентны (обратите внимание, что угловая минута и угловая секунда обозначены галочкой и двойной отметкой соответственно):
В настоящее время существует тенденция использовать десятичное представление для дробной части градуса, но иногда все еще используются минуты и секунды. Следующие значения углов эквивалентны (обратите внимание, что угловая минута и угловая секунда обозначены галочкой и двойной отметкой соответственно):
45,16 °
45 ° 9 ’36 »
радиан — это угол, стянутый в cen tre окружности дугой окружности, длина которой равна радиусу окружности.Преобразование между углами, измеренными в градусах, и углами, измеренными в радианах, относительно несложно. Поскольку общая длина окружности равна 2π r , и поскольку один радиан — это угол, образованный дугой окружности длиной r , то значение одного радиана в градусах определяется как:
| один радиан = | 360 | = 57,296 ° |
| 2π |
И наоборот, значение одного градуса в радианах определяется как:
| один градус = | 2π | = 0. 017 радиан 017 радиан |
| 360 |
Для задач, связанных с тригонометрией, значение угла может быть указано в градусах или радианах. Поэтому полезно знать, как конвертировать между ними, если возникнет такая необходимость. Имейте в виду, что большинство научных калькуляторов могут выполнять тригонометрические вычисления в градусах или радианах. Вы должны убедиться, что ваш калькулятор установлен в правильный режим при использовании тригонометрических функций, иначе вы можете получить неожиданные результаты.Калькулятор Microsoft Windows (находится в Программы> Стандартные ) в режиме Scientific может быть установлен на градусов , радиан, или градусов , выбрав соответствующий переключатель (градиент — редко используемая единица измерения угла, равная одной четырехсотой оборота).
Калькулятор Microsoft Windows может быть установлен на градусов , радиан или градусов
Продолжение использования градуса в качестве единицы измерения угла в наше время может показаться немного странным, если принять во внимание тот факт, что он возник несколько тысяч лет назад. Деление круга на триста шестьдесят частей обычно приписывается вавилонским астрономам. Число было выбрано, вероятно, потому, что оно совместимо с шестидесятеричной системой счисления , используемой вавилонянами, и потому что оно почти совпадает с количеством дней в году. Оказывается, триста шестьдесят (360) на самом деле очень удобное число для работы, потому что оно позволяет представить различные общие доли круга с использованием целого числа градусов.
Деление круга на триста шестьдесят частей обычно приписывается вавилонским астрономам. Число было выбрано, вероятно, потому, что оно совместимо с шестидесятеричной системой счисления , используемой вавилонянами, и потому что оно почти совпадает с количеством дней в году. Оказывается, триста шестьдесят (360) на самом деле очень удобное число для работы, потому что оно позволяет представить различные общие доли круга с использованием целого числа градусов.
С другой стороны, радиан часто считается естественной единицей измерения углов при работе с тригонометрическими функциями. Причина в том, что зачастую это просто удобнее. Число радианов в полном вращении равно 2π. Тригонометрические функции часто используются для решения уравнений, в которых в качестве фактора используется член 2π. Работа в радианах часто означает, что мы можем полностью исключить член 2π из наших вычислений, упростив решение уравнения и уменьшив влияние ошибок округления. Если результат должен быть выражен в градусах , преобразование может быть выполнено в конце, после того, как все вычисления будут завершены.
Если результат должен быть выражен в градусах , преобразование может быть выполнено в конце, после того, как все вычисления будут завершены.
В следующей таблице показано графическое представление нескольких часто встречающихся углов в виде долей круга вместе с их значениями, выраженными как в градусах, так и в радианах. Знакомство с этими углами, хотя это не является строго необходимым для изучения тригонометрии, может помочь студентам понять взаимосвязь между градусами и радианами.Это также может способствовать лучшему пониманию того, как на самом деле работают различные тригонометрические функции. Для показанных углов мы приняли соглашение, согласно которому начальная сторона угла угла является осью x в декартовой плоскости, а все углы равны положительным углам (т. Е. Угол поворота измеряется против — по часовой стрелке от начальной стороны к стороне вывода (). Обратите внимание, что значения в радианах выражены в единицах пи (π). Это обеспечивает большую точность, чем эквивалентные десятичные представления.
Это обеспечивает большую точность, чем эквивалентные десятичные представления.
Определить размер угла относительно легко, если угол образован двумя отрезками линии или лучами, которые сходятся в центре круга известного радиуса, а дуга, образующая угол (известная как центральный угол ), может быть измеряется. Рассмотрим иллюстрацию ниже. Угол θ — это центральный угол, образованный дугой s в центре окружности с радиусом r .Если у нас есть значения для r и s , мы можем найти угол θ .
Дуга с расширяет угол θ
Значение угла θ в радианах определяется по формуле:
| θ = | с | радиан |
| r |
Мы также можем найти значение θ в градусах, используя:
| θ = | 360 с | градусов |
| 2π r |
И наоборот, вы, вероятно, можете видеть из вышеизложенного, что если мы знаем радиус круга и значение угла θ в радианах, мы можем найти длину дуги s следующим образом:
с = r θ
Если значение угла θ задано в градусах, длина дуги s будет:
Учтите, что размер угла не зависит от длины его сторон. Представьте себе положительный угол, нарисованный в плоскости x — y , вершина которого находится в начале системы координат (0, 0), причем начальная сторона угла совпадает с осью x , как показано на иллюстрации ниже. Стороны треугольника могут бесконечно отходить от вершины.
Представьте себе положительный угол, нарисованный в плоскости x — y , вершина которого находится в начале системы координат (0, 0), причем начальная сторона угла совпадает с осью x , как показано на иллюстрации ниже. Стороны треугольника могут бесконечно отходить от вершины.
Стороны угла могут бесконечно уходить от вершины.
Чтобы вычислить значение угла θ , нам нужны числа для работы.Конечно, мы могли бы найти координаты x и y двух точек на конечной стороне угла, а затем использовать алгебру, чтобы найти наклон прямой (см. Страницу «Линейные уравнения» в книге Algebra раздел). Это даст нам тангенс угла θ , и мы могли бы использовать функцию arctan на калькуляторе, чтобы найти угол. Это, однако, забегает вперед. А пока мы попробуем найти угол, фактически не используя тригонометрические функции. Мы можем начать с рисования окружности известного радиуса с центром в начале системы координат (которая также является вершиной угла θ ). На иллюстрации ниже добавлена окружность радиуса r = 2. Дуга, которая образует угол θ , показана красным.
Мы можем начать с рисования окружности известного радиуса с центром в начале системы координат (которая также является вершиной угла θ ). На иллюстрации ниже добавлена окружность радиуса r = 2. Дуга, которая образует угол θ , показана красным.
Угол θ образует дугу окружности радиуса r = 2 с центром в начале координат.
Мы знаем радиус круга (так как мы его выбрали!), Поэтому все, что нам нужно сделать, это измерить длину дуги, и тогда у нас будет достаточно информации для вычисления угла.Однако измерить длину дуги не так-то просто. Вероятно, поэтому древние греки предпочли использовать хорды для измерения углов, образованных дугой окружности. Хорда — это отрезок прямой, соединяющий две точки на окружности круга. Если эти две точки совпадают с концами дуги, говорят, что хорда соединяет дугу. Хорда, которая образует дугу, естественно, образует один и тот же центральный угол, но ее легче измерить, потому что это прямая линия.Для любого заданного центрального угла соотношение хорды, которая образует угол, и диаметра круга будет постоянным значением. Греки использовали этот факт, чтобы разработать метод измерения углов. На странице под названием «Аккорды» в этом разделе эти концепции рассматриваются более подробно.
Хорда, которая образует дугу, естественно, образует один и тот же центральный угол, но ее легче измерить, потому что это прямая линия.Для любого заданного центрального угла соотношение хорды, которая образует угол, и диаметра круга будет постоянным значением. Греки использовали этот факт, чтобы разработать метод измерения углов. На странице под названием «Аккорды» в этом разделе эти концепции рассматриваются более подробно.
Введение в стандартные единицы измерения США
Введение в стандартные единицы измерения США
Также известны как «английские единицы» или «обычные единицы США»
Вау, я только что прилетел с планеты Микрон.Это был долгий полет, но он того стоил, чтобы провести с вами время!
Меня зовут Мэгги на вашем языке (но вы не можете произнести мое настоящее имя!)
Когда я только приехал, я не мог понять, как вы измеряете вещи, но мой друг Том научил меня измерению, и я собираюсь поделиться с вами всем, чему он меня научил.
Первое, что сказал мне Том, это то, что вы можете измерять вещи, используя две разные системы: стандартных единиц США, и метрическую систему.
Сегодня мой день, чтобы выучить стандартные единицы США!
Жидкости
Поскольку это был такой долгий перелет, первое, что я мог использовать, — это что-нибудь холодное, чтобы выпить. Но я хочу быть уверен, сколько просить! Так что я могу получить не слишком большой или не слишком маленький напиток. |
Первое, что мне нужно знать при запросе напитка, — это единиц измерения , используемых для измерения жидкостей, а именно:
- Унции жидкости
- Чашки
- Пинты
- Кварты
- галлонов
Жидкие унции (унции) маленькие . Примерно сколько помещается в маленькую чашечку с лекарством … но этого недостаточно для того, кто хочет пить! |
| Затем Том показал мне небольшую коробку и сказал, что в ней 8 жидких унций, что также называется 1 чашка . Но хотелось большего! |
Итак, Том показал мне пинты , что равняется 2 чашкам. Это казалось подходящим для того, кто очень хотел пить! |
(Том также сказал мне, что я могу измерять предметы с помощью мерных стаканчиков)
Чтобы отмерить несколько стаканов жидкости вместе, вы можете использовать кварты. кварта (кварты) — это то же самое, что 4 чашки или 2 пинты. |
Если вам все еще нужно больше жидкости, вы можете переключиться на использование галлонов. галлонов (галлон) — это то же самое, что 16 чашек, 8 пинт или 4 квартов. Это самое крупное измерение жидкости. (Ого! Кварта — это четверть галлона!) |
Итак, теперь я знаю, что 1 унция для меня слишком мало, а 1 галлон — слишком много. Думаю, я попрошу пинту сока!
Заключительные мысли об измерении жидкостей:
1 галлон = 4 кварты = 8 пинт = 16 чашек = 128 жидких унций
Масса (вес)
Затем я хотел съесть немного шоколада… так что я должен узнать о массе. Вы часто называете это «весом», но предметы имеют вес только из-за гравитации на вашей планете!
Том говорит, что мне нужно знать:
Унции снова! Меня действительно смутило то, что когда я просил выпить, я мог использовать унции, но унции также используются для измерения массы . … одно и то же слово может использоваться в двух разных системах измерения! Как это удивительно? Но они действительно разные. |
Том говорит:
Если вы имеете в виду унцию жидкости, скажите «жидкая унция» («жидкая унция»)
В противном случае унция обычно означает массу.
Так что мы не говорим о жидкостях! Я уже выпил. Мне нужно знать о массе.
Наименьшая единица массы — унций (унций). Кусок хлеба весит около одной унции. Он очень легкий. |
Но когда вы складываете унции, вы получаете новую этикетку для массы:
Если у вас 16 унций, его также можно назвать фунтом (фунт). Как правило, это единица измерения собственного веса. 1 фунт = 16 унций фунтов используются для измерения множества вещей, от людей до еды и животных. Том говорит, что он весит 90 фунтов. |
Но если что-то весит много фунтов, мы используем еще один ярлык
2000 фунтов — это тоже одна тонн . 1 тонна = 2000 фунтов Это действительно тяжело! Грузовики, корабли и тяжелое оборудование измеряются в тоннах, а не в фунтах. Слон имеет массу около 8 тонн ! |
Итак, теперь я знаю, что 1 унция шоколада для меня слишком мала, но 1 тонна — это слишком много.Думаю, я попрошу фунт шоколада!
Заключительные мысли о массе:
1 фунт = 16 унций
1 тонна = 2000 фунтов = 32000 унций
Длина
Последний вид измерения, который мы рассмотрим, — это длина. Это важно по разным причинам. Измерение длины помогает узнать, как далеко вы прошли, как далеко вам осталось пройти, какой у вас рост и многое другое.
Это важно по разным причинам. Измерение длины помогает узнать, как далеко вы прошли, как далеко вам осталось пройти, какой у вас рост и многое другое.
Мне нужно знать о:
Малые единицы длины называются дюймов . Последний сустав вашего пальца или большого пальца составляет около 1 дюйма (в зависимости от размера ваших пальцев!). |
Многие вещи измеряются в дюймах от дождя до длины бумаги.
Измерение в дюймах дает нам возможность понять размер чего-либо.
Когда у нас 12 дюймов вместе, это называется футов .
1 фут = 12 дюймов
Давным-давно люди измеряли вещи ногами. Но у всех ноги разного размера, так что это не сработало.
Использование 12 дюймов, взятых вместе, чтобы сделать одну ногу, позволяет каждому получить точное представление о том, что такое «фут» длины.
Когда 3 фута вместе, это называется ярдом. (Это не то же самое, что газон, хотя оба они называются «двором»!)
(Это не то же самое, что газон, хотя оба они называются «двором»!)
1 ярд = 3 фута
Длина гитары около 1 ярда.
Когда вы складываете 1760 ярдов, вы получаете миль .
1 миля = 1760 ярдов = 5280 футов
мили — это большие расстояния, которые в основном используются для измерения расстояния между местами, которые находятся далеко друг от друга. Большинство людей называют мили, когда они едут за рулем, ездят на велосипеде или бегают трусцой.
Заключительные мысли об измерении длины:
1 фут = 12 дюймов
1 ярд = 3 фута = 36 дюймов
1 миля = 1760 ярдов = 5280 футов = 63360 дюймов
Температура
Мне стало немного жарко, поэтому я спросил Тома, как измерить температуру.
И он показал мне градусник . А вот увидел 2 набора номеров !
А вот увидел 2 набора номеров !
Том объяснил, что термометр измеряет в градусах (°) Цельсия или Фаренгейта.
«Почему две шкалы?» — спросил я.
Том сказал, что некоторым нравится одна шкала, а некоторым — другая, и что я должен изучить обе!
Затем он привел мне пример: когда вода замерзает, термометр показывает:
- 0 градусов Цельсия слева,
- , но с правой стороны он показывает 32 градуса по Фаренгейту .
Два числа для одного и того же!
Он привел мне еще примеры.
- Жаркий солнечный день с температурой 30 градусов по Цельсию составляет 86 градусов по Фаренгейту .
- Вода закипает при 100 градусах Цельсия или 212 градусах Фаренгейта .
- И вы можете испечь вместе
Единица измерения
В «Измерении» мы говорим о «Единицах» … что они такое?
Единица измерения — это любое единичное измерение.
Итак, 1 метр — это единица измерения.
И 1 секунда также является единицей
И 1 м / с (один метр в секунду) тоже единица, потому что есть одна из них.
И так далее …
Без «1»
Также принято оставлять «1» впереди и просто говорить о типе измерения как единице.
Пример: обычно используемой единицей времени является секунд
Мы не говорим, что секундомер измеряет «1 секунду», мы говорим, что он измеряет «секунды».
Итак, «Единица» — это общий термин, обозначающий тип измерения. И люди понимают, что мы имеем в виду только «1».
Значит, разговор может быть таким
Алекс: «Измеряет 100»
Сэм: «В каком блоке?»
Алекс: «Сантиметры»
Пример: спидометр
Какой прибор измеряет этот спидометр? Он измеряет км / ч (километров в час) Итак, «220» означает 220 километров в час. |
Сокращение
Обычно мы пишем единицы, используя их сокращения.
Пример: км на километр
Пример: м / с (или мс -1 ) для метра в секунду
м / с — единица скорости
Пример: кг / м 3 (или кг / м -3 ) на килограмм на кубический метр
кг / м 3 — единица плотности: сколько массы в единице объема.
Стандартизированный
Единицы измерения «стандартизированы», что означает, что существует четко определенный стандарт для измерения 1 из них.
Пример: В течение многих лет (с 1889 по 1960) существовала планка International Prototype Met re , чтобы точно показывать людям, что такое 1 метр.
Но этого было недостаточно!
Теперь «1 метр» определяется как расстояние, которое проходит свет за 1 / 299 792 458 секунды.
Различные системы измерения
Единицы можно сгруппировать в «Систему».
Цена за единицу
Цена за единицу указывает нам стоимость литра, килограмма, фунта и т. Д. Того, что мы хотим купить.
Это хороший способ сравнить стоимость того, что мы покупаем.
Пример: что лучше
- 2 литра молока по цене 3,80 доллара США, или
- 1,5 литра молока по 2,70 доллара?
В данном случае «Единица» — 1 литр, а Цена единицы:
- 3 доллара.80/2 литра = 1,90 $ за литр
- 2,70 $ / 1,5 литра = 1,80 USD за литр
Итак, самая низкая цена за единицу (и лучшая сделка) составляет 1,5 литра по 2,70 доллара.
Единица измерения — Простая английская Википедия, бесплатная энциклопедия
Единицы измерения предоставляют стандарты , так что числа из наших измерений относятся к одному и тому же. Измерение — это процесс, который использует числа для описания физической величины.Мы можем измерить, насколько большие вещи, насколько они теплые, насколько они тяжелые, а также множество других функций.
Например, метр — это стандартная единица измерения длины. До 1982 года оно определялось как расстояние между двумя маркерами на специальной рейке. Теперь ученые определяют метр, используя скорость света. Сказать, что что-то имеет длину два метра, означает, что это ровно в два раза больше, чем длина стержня, используемого для определения метра.
В прошлые века в разных странах использовалось много разных единиц измерения.Сегодня большинство единиц измерения относятся к одной из трех систем:
Две старые, британская имперская система и тесно связанная с ней обычная система США, используют стопу как меру длины, фунт как меру веса, а второй — как меру времени. Они также используют другие единицы. Количество меньших единиц, из которых состоят большие единицы в этих двух системах, варьируется: например, 12 дюймов в футе и 16 унций в фунте.
Самая новая и наиболее используемая из трех систем — это метрическая система или система СИ, в которой используется 10, 100 или 1000 единиц меньшего размера для создания большей. Например, в одном метре 100 сантиметров или в килограмме 1000 граммов. Эта система использует метр для длины и килограмм для массы.
Например, в одном метре 100 сантиметров или в килограмме 1000 граммов. Эта система использует метр для длины и килограмм для массы.
Обычное неметрическое измерение времени не следует этому шаблону. Второй является основой для измерения времени, и он основан на шестидесятеричной системе счисления: 60 секунд составляют одну минуту, а 60 минут составляют один час.
Свойство измеряемой вещи выражается в количестве единиц измерения. Число имеет смысл только тогда, когда указана единица измерения.
Например, Эйфелева башня в Париже, Франция, имеет высоту 300 метров (980 футов). [1] То есть расстояние от верха до низа Эйфелевой башни составляет 300 метров. Свойство измеряемой Эйфелевой башни — это расстояние. Было измерено 300. 300 из которых? Единица измерения — метр.
Стандарты — это специальные объекты, которые используются для проведения измерений. Метр — пример стандарта. Когда вы измеряете что-либо с помощью измерительной линейки, вы можете сравнить это измерение с чем-либо еще, что также измеряется с помощью измерительной линейки. Это упрощает измерения и упрощает сравнение результатов измерений.
Это упрощает измерения и упрощает сравнение результатов измерений.
В науке, медицине и технике используются меньшие единицы измерения для измерения мелких вещей с меньшими ошибками. Большие предметы легко измерить, используя большие единицы измерения. В астрономических измерениях, таких как ширина галактики, используются световые годы и парсеки.
В малых измерениях, таких как масса атома, используются специальные единицы измерения.
Во всем мире используется множество различных стандартов и единиц измерения.Некоторые стали меньше использоваться в 19 и 20 веках.
Метрическая система [изменить | изменить источник]
Метрическая система — это система измерения, используемая в большинстве стран мира. Ее также называют Международной системой единиц или СИ.
Единицы измерения в метрической системе включают:
- Единица измерения — литр. Он используется для измерения количества жидкости. Миллилитр (сокращенно мл ) — это количество жидкости, которое может заполнить куб размером 1 сантиметр с каждой стороны.
 Один литр жидкости заполнит куб размером 10 см с каждой стороны.
Один литр жидкости заполнит куб размером 10 см с каждой стороны.
- Единицей массы является килограмм. Килограмм ( кг, ) — это масса 1 литра воды (при температуре 4 ° C или 39 ° F и давлении 1013,25 кПа или 146,959 фунтов на квадратный дюйм). 1 грамм ( г ) — это масса 1 миллилитра воды при 4 ° C (39 ° F). Метрическая тонна составляет 1000 килограммов или миллион граммов.
Британские единицы [изменить | изменить источник]
имперских единиц были определены в Великобритании в 1824 году.Эти единицы были основаны на аналогичных единицах, которые использовались до 1824 года. Имперские единицы использовались в странах, которые были частью Британской империи. Хотя многие из этих стран, включая Соединенное Королевство, официально приняли СИ, старая система единиц все еще используется.
Традиционные единицы США [изменить | изменить источник]
обычных единиц измерения США — официальные единицы, используемые в США. Они похожи на британские имперские единицы, а также основаны на единицах, используемых в Соединенном Королевстве до независимости США. Некоторые подразделения отличаются от британских. Например, в имперской пинте 20 имперских жидких унций, а в американской пинте — 16 американских жидких унций. Кроме того, жидкая унция США немного больше имперской жидкой унции. В результате пинты и галлоны США меньше английских пинт и галлонов. В Соединенных Штатах метрическая система является законной для торговли с 1866 года, но другие измерения, такие как галлон, дюйм и фунт, все еще широко используются.
Некоторые подразделения отличаются от британских. Например, в имперской пинте 20 имперских жидких унций, а в американской пинте — 16 американских жидких унций. Кроме того, жидкая унция США немного больше имперской жидкой унции. В результате пинты и галлоны США меньше английских пинт и галлонов. В Соединенных Штатах метрическая система является законной для торговли с 1866 года, но другие измерения, такие как галлон, дюйм и фунт, все еще широко используются.
Имперские и американские единицы измерения включают:
- Длина — дюйм ( дюймов, ), фут ( футов, ), ярд ( ярдов, ) и миля.
- 1 фут = 12 дюймов
- 1 ярд = 3 фута (множественное число футов) = 36 дюймов
- 1 миля = 1760 ярдов = 5280 футов
- Объем США — жидкая унция США ( жидких унций ), чашка США ( cp ), пинта США ( pt ), кварта США ( qt ) ) и галлон США ( галлонов ).
- 1 чашка США = 8 жидких унций США
- 1 пинта США = 2 чашки США = 16 жидких унций США
- 1 кварта США = 2 пинты США = 4 чашки США = 32 жидкие унции США
- 1 галлон США = 4 кварты США = 8 пинт США = 16 чашек США
- Вес и масса — унции ( унций ), фунты ( фунтов ) и камень ( st ).
- 1 фунт = 16 унций
- 1 камень = 14 фунтов
Унции для веса и объема различаются. Даже при измерении воды количество унций веса не совпадает с количеством жидких унций.
Преобразование между системами [изменить | изменить источник]
- Метрическая система по США
- 1 метр = 1,09 ярда = 39,37 дюйма.
- 1 литр = 33,3 жидких унций = 1,76 пинты = 0,26 галлона США.
- 1 килограмм = 35.32 унции = 2,2 фунта
- Метрическая система США
- Длина
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 ярд = 0,9144 метра
- 1 миля = 1,609344 километра
- Объем
- 1 жидкая унция = 29,6 миллилитра
- 1 пинта = 473,1 миллилитра
- 1 галлон = 3,79 литра
- 1 чашка = 236,55 миллилитра
- Масса
- 1 унция = 28.35 граммов
- 1 фунт = 0,45359237 килограмма
Единица времени — секунда. Минута (60 секунд) и час (60 минут или 3600 секунд) — большие единицы. День определяется как 24 часа, но вращение Земли замедлилось. Разница корректируется в конце нескольких лет с помощью так называемой дополнительной секунды. Неделя (7 дней) и месяц также являются стандартными единицами.
Единица измерения, применяемая к деньгам, называется расчетной единицей. Обычно это валюта, выпущенная страной.Например, в США используются доллары. Каждый доллар составляет 100 центов. Соединенное Королевство использует фунты. Каждый фунт равен 100 пенни или пенсу. Европейский Союз использует евро. В евро 100 центов.
Единицы измерения электричества, магнетизма и излучения в основном изобрели в 19 веке, когда ученые научились их измерять. Большинству из них изначально были присвоены имперские системы, но сегодня для них обычно используются метрические системы.
- ↑ Можно также сказать: «Высота Эйфелевой башни 300 метров».
ГЕОМЕТРИЯ — Тематические тексты
Главная → ГЕОМЕТРИЯ — Тематические текстыТекст 1
Геометрия позволяет нам исследовать свойства пространства в терминах плоских (двухмерных) фигур и твердых (трехмерных) фигур. Мы можем использовать геометрические методы, чтобы нарисовать линию точной длины, разрезать линию пополам, разделить пополам угол, построить треугольник и вычислить площадь сферы. Принципы геометрии заложил греческий математик Евклид (К.330 г. до н.э. — 275 г. до н.э.) и с тех пор почти не изменились. Картографирование; Геодезия, проектирование, архитектура и компьютерные схемы — все зависит от геометрии в точном использовании углов, фигур и объема.
Текст 2
Треугольники, квадраты и пятиугольники — все это примеры многоугольников. У правильного многоугольника стороны равной длины и внутренние углы равны. Чем больше сторон у правильного многоугольника, тем больше он будет напоминать круг. Есть два вида многоугольников: выпуклые и входящие.У выпуклого многоугольника все углы направлены внутрь. У входящего многоугольника один или несколько углов направлены внутрь.
Текст 3
Углы образуются на стыке двух прямых линий. Их можно измерить с помощью транспортира или указателя угла. Углы измеряются в единицах, называемых градусами. Градус получается делением окружности круга на 360 частей равного размера. Математики используют маленький кружок в качестве символа для обозначения градусов. Угол, возникающий в углах квадратов и других прямоугольников, составляет 90 градусов и называется прямым углом.Углы меньше 90 называются острыми углами. Углы от 90 до 180 называются тупыми. Углы от 180 до 360 называются углами отражения.
Текст 4
Преобразование — это изменение положения, размера или формы геометрической фигуры (например, треугольника). Основные преобразования — это отражение, увеличение, перемещение и вращение. Другие формы трансформации включают растяжение и сдвиг. Отражение, перемещение и вращение изменяют положение фигуры.Они не изменяют длину сторон или площадь фигуры, и поэтому называются изометриями. Растяжка увеличивает размер фигуры по одной оси. Стрижка похожа на растяжку, но площадь фигуры остается прежней. Увеличение увеличивает размер всей фигуры.


 Несколько фактов из истории
Несколько фактов из истории В круге 400 градусов, значит, прямой угол равен 100 градусам.Вы редко увидите этот агрегат. Думайте об оценках как о «метрических градусах».
В круге 400 градусов, значит, прямой угол равен 100 градусам.Вы редко увидите этот агрегат. Думайте об оценках как о «метрических градусах».

 ..
..

 Один литр жидкости заполнит куб размером 10 см с каждой стороны.
Один литр жидкости заполнит куб размером 10 см с каждой стороны.