Выпуклый, невыпуклый и звездчатый многоугольник

Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником. На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника; сумма длин сторон АВ + ВС + CD + … + FA называется периметром и обозначается р, а иногда 2р (тогда р — полупериметр).

рис.1

В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.

Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками

. На рис.2 изображен звездчатый многоугольник ABCDE.

рис.2

Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым.

Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).

рис.3

Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2), где n — число сторон многоугольника*.

* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°. Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.

★ Шестиугольник — cтатьи по математике .

. Информация

Пользователи также искали:

неправильный шестиугольник, периметр шестиугольника, площадь шестиугольника, правильный шестиугольник формулы, радиус шестиугольника, шестиугольник вписанный в окружность, сторона правильного шестиугольника вписанного в окружность, выпуклый шестиугольник, шестиугольника, Шестиугольник, шестиугольник, окружность, радиус, площадь шестиугольника, периметр шестиугольника, шестиугольник вписанный в окружность, выпуклый шестиугольник, радиус шестиугольника, правильный шестиугольник формулы, правильный, площадь, периметр, вписанный, сторона, правильного, вписанного, выпуклый, формулы, неправильный, неправильный шестиугольник, сторона правильного шестиугольника вписанного в окружность, cтатьи по математике.

\circ}{n}\).

Как начертить правильный шестиугольник с помощью циркуля

Урок 35. Геометрия 9 класс

Конспект урока «Построение правильных многоугольников»

На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Для выполнения построений мы используем циркуль и линейку.

– построить дугу окружности,

– отложить на прямой отрезок, равный данному.

– построить прямую линию,

– построить отрезок, соединяющий две точки,

– найти точку пересечения двух прямых.

Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.

Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.

Задача 1. Вписать в заданную окружность правильный треугольник

Построение. Пусть задана окружность с центром О. Проведем произвольный диаметр BD окружности. Построим прямую l, являющуюся серединным перпендикуляром к радиусу OD. Середину радиуса ОD обозначим точкой К. Отметим точки А и C – пересечения прямой l с окружностью. И построим отрезки BA и BC. Треугольник ABC – правильный.

В Тогда Отсюда, .

Значит,

Задача 2. Вписать в заданную окружность правильный четырехугольник.

Построение. Пусть задана окружность с центром О. Построим диаметр AC. Затем построим диаметр BD перпендикулярный диаметру AC. Точки А, C и B, D – точки пересечения диаметров с окружностью. И построим отрезки АB, BC, CD и АD. Четырехугольник ABCD – правильный.

Т.к. Т.к. Т.к. Т.к. Следовательно, – квадрат.

Значит, – правильный четырехугольник.

Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.

Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.

Построение. Так как в правильном шестиугольнике сторона а равна радиусу, то достаточно последовательно отложить от одной точки окружности 6 радиусов-хорд. Пусть МN – заданный отрезок. Построим окружность с произвольным центром О и радиуса MN. Отметим на этой окружности произвольную точку А. Затем, не меняя раствора циркуля, последовательно от этой точки А будем делать на окружности засечки, пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим точки B, C, D, Е и F. Теперь соединим последовательно построенные точки отрезками. Получим искомый правильный шестиугольник ABCD.

Равные хорды стягивают равные дуги.

Все углы шестиугольника будут равны, так как опираются на дуги, состоящие из четырех равных меньших дуг.

Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.

Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.

Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.

1. 2. Окружность .

3. – серединные

перпендикуляры к .

4.

.

5. – правильный двенадцатиугольник.

Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырехугольник, т.е. квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник, затем правильный шестнадцати-угольник и вообще правильный 2 k угольник, где k – любое целое число, большее 2.

Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.

С давних времен построению правильных многоугольников математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники. А также многоугольники, получаемые удвоением их сторон, шестиугольники, восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000 лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли «королем математики», решил эту математическую проблему. Будучи девятнадцати летним юношей, он доказал, что можно построить правильный семнадцати-угольник, а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник циркулем и линейкой построить нельзя. Задача о построении правильного семнадцати-угольника была самым первым его научным открытием.

Подведем итоги урока.

Сегодня мы рассмотрели способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились строить правильные треугольник и четырехугольник, вписанные в окружность. А также выполнили задачу на построение правильного многоугольника по заданному отрезку, и задачу на построение правильного 2n-угольника по заданному n-угольнику.

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Понимая самые простые закономерности в геометрии, можно научиться строить на плоскости более сложные фигуры. Так, большинство геометрических фигур имеют достаточно сложный вид, однако, зная определённые правила, можно понять, как построить шестиугольник с помощью только лишь циркуля и линейки.

Для начала на листе бумаги необходимо изобразить окружность, делается это с помощью циркуля. Устанавливаем ножки инструмента на определённом уровне друг от друга, чтобы задать радиус, после чего рисуем окружность. Важно помнить, что окружность должна полностью помещаться на листе бумаги. При этом, если ножки циркуля будут сильно близко друг к другу или, наоборот, сильно далеко друг от друга, то может не получиться начертить правильную окружность. Поэтому стоит учитывать, что между ножками должен быть угол примерно в 30 градусов.

Теперь необходимо построить точки, которые будут являться вершинами углов шестиугольника. Для этого, не меняя расстояния между ножками циркуля, устанавливаем иглу в любую точку окружности таким образом, чтобы игла была точно на линии. Чем точнее будут выполнены действия, тем точнее будет дальнейшее построение. Теперь проводим циркулем дугу до тех пор, пока она не пересечётся с линией окружности. Это и будет одной из вершин углов шестиугольника. Далее переставляем иглу в только что полученную точку и совершаем такие же действия. Эту операцию нужно будет проделать ещё четыре раза, в результате чего получится шесть точек, то есть шесть углов.

Перед тем как построить правильный шестиугольник, необходимо соединить полученные точки. Все действия необходимо делать с помощью карандаша и линейки, чтобы добиться максимально точного результата. В итоге на листе бумаги появится вписанный в окружность правильный шестиугольник.

Шестиугольник, виды, свойства и формулы

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

.

Размеры

Чтобы отвертка прослужила долго, и не стерлась, важно выбрать правильный размер инструмент с нужным наконечником.

Для каждого вида разработаны специальные стандарты размеров, и присвоены им номерные обозначения.

Шлицевые отвертки с плоской формой наконечника могут иметь ширину от 2 до 18 мм, а крестообразные модели идут с нумерацией от 0 до 4.

Все номерные виды рассчитаны на определенный диаметр наружной резьбы:

• № 0 – до двух мм; • № 1 – от двух до трех мм; • № 2 – от трех до пяти мм; • № 3 – от пяти до семи мм и т.д.

Размеры стержня зависят от номера отвертки.

Так, например, нулевая отвертка имеет диаметр стержня 4 миллиметра при длине до 80 миллиметров.

По мере возрастания номера увеличивается диаметр и длина стержня.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Торцевые гаечные ключи

Этот вид ключей представляет собой полую трубку или цилиндр с углублениями на обоих концах. Торцевые ключи бывают двух типов:

Г-образные торцевые ключи

Они имеют одинаковый размер на обоих краях рабочих частей. Это сделано с тем расчетом, что гайка (или болт) могут находиться глубоко от поверхности и тогда используется длинная часть ключа, но при этом необходимо приложить больше усилий (из-за маленького рычага). Если деталь находится неглубоко, тогда используется короткая часть ключа, соответственно из-за большего рычага усилий прикладывается меньше.

I-образные гаечные ключи

Выглядят как полый цилиндр с рабочей частью разного размера на обоих концах. Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа.

Виды молотков и их назначение

Шестигранные ключи

Этот вид ключей имеет Г-образную форму и используется для работы с болтами (шурупами, винтами) имеющими не внешние грани, а внутренние. В основном применяются в основном при сборке мебели, ремонте бытовой технике и подобных работах.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a1 = a2 = a3 = a4= a5= a6.

2. Все углы равны между собой и составляют 120°.

α1 = α2 = α3 = α4 = α5 = α6 = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

R = a

Накидные ключи

У этих ключей рабочая часть имеет фору кольца с гранями на внутренней стороне. Его конструкция более надежна чем у рожковых ключей, так как деталь охватывается по всей поверхности (то есть как минимум в шести местах), что практически исключает деформацию углов. Накидные ключи существуют с двумя типами внутреннего профиля – с 6-и гранным профилем и 12-и гранным профилем. Профилем с 12-ю гранями работать в ограниченном пространстве удобней, так как ему достаточно поворота на 30 градусов, к ключу с 6-и гранным профилем необходимо 60 градусов поворота.

Чистый двор и дом — мойка высокого давления!

Более распространенны ключи с наклонной головкой, когда рабочая часть находится под небольшим углом к рукоятке. Накидные ключи выпускаются разного размера, как и рожковые ключи.

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Виды отверток и их назначение

Универсальная отвертка слесарная – это инструмент, который есть практически в каждом доме.

Благодаря отвертке можно выполнять ремонтные работы разной степени сложности, главное знать, какой тип и диаметр подойдет в каждом конкретном случае.

О том, какие бывают отвертки можно узнать, если детальнее углубиться в тему.

Отличительной особенностью всех видов является разное толщина стержня.

Читать также: Как проверить акб без нагрузочной вилки

Наиболее популярными считают отвертки с круглым и квадратным сечением, с прямым или крестообразным шлицем.

Однако технический прогресс не стоит на месте и наряду с новыми видами крепежа появляются профессиональные отвертки для вкручивания болтов, шурупов и прочих элементов.

Все это делается для того, чтобы облегчить работу потребителям.

• На данный момент кроме универсальных моделей существует еще несколько модернизированных видов отверток для проведения разных работ.

Например, переставная отвертка отличается своей универсальностью, т.к. с одной стороны стержня она плоская, а с другой крестовая.

Некоторые переставные модели имеют несколько разных наконечников, что повышает универсальность инструмента.

• Точная или как ее еще называют, тонкая отвертка – подойдет для ремонта мобильных телефонов, ее маркировка соответствует нулевому обозначению.

Изделие производят с малым размером шлица, не более 2мм, что позволяет выполнить точную работу с мелкими деталями.

• Особые эргономичные свойства приобрела двухкомпонентная отвертка, ее отличительной особенностью стала прочная рукоять из комбинированных материалов.

Для покрытия рукояти использовали полипропилен и резину.

Двухкомпонентное покрытие способствует надежному захвату, чтобы изделие уже не могло выскользнуть из рук.

• Для работы с тонкими деталями используют часовые отвертки, с их помощью ремонтируют часовые механизмы.

Размер наконечника изделия – не более миллиметра.

На этом классификация профессиональных монтажных отверток не заканчивается, существует еще много разновидностей моделей, предназначенных для определенных целей.

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

R = a

Маркировка и размеры [ править | править код ]

Ключи и отвёртки имеют маркировку T

или
TX
с номером шлица — 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20, 25, 27, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100.

Ключи и отвёртки со шлицом Torx Tamper Resistant

после основной маркировки дополнительно обозначаются
TR
.

У ключей и отвёрток со шлицом Torx Plus

сначала указывается номер шлица, а после — вместо
T
или
TX
обозначается буквами
IP
.

Ключи и отвёртки со шлицом Torx Plus Tamper Resistant

после основной маркировки дополнительно обозначаются
TS
.

Размер определяется по диаметру окружности описанной по вершинам звездочки инструмента (для версии E — болта).

Приблизительные размеры и моменты затяжки [3]

Номер

Размер

Момент затяжки

E Torx

дюймы	мм	Н•м
T1	0,031″	0,81	0,02 — 0,03
T2	0,036″	0,93	0,07 — 0,09
T3	0,046″	1,10	0,14 — 0,18
T4	0,050″	1,28	0,22 — 0,28
T5	0,055″	1,42	0,43 — 0,51
T5.5 [4] [5] [6]
T6	0,066″	1,70	0,75 — 0,90
T7	0,078″	1,99	1,4 — 1,7
T8	0,090″	2,31	2,2 — 2,6
T9	0,098″	2,50	2,8 — 3,4
T10	0,107″	2,74	3,7 — 4,5
T15	0,128″	3,27	6,4 — 7,7
T20	0,151″	3,86	10,5 — 12,7	E4
T25	0,173″	4,43	15,9 — 19	E5
T27	0,195″	4,99	22,5 — 26,9
T30	0,216″	5,52	31,1 — 37,4	E6
T35 [7] [8] [9]
T40	0,260″	6,65	54,1 — 65,1	E8
T45	0,306″	7,82	86 — 103,2
T47 [10] [11]	GM-Style
T50	0,346″	8,83	132 — 158	E10
T55	0,440″	11,22	218 — 256	E12
T60	0,519″	13,25	379 — 445	E16
T70	0,610″	15,51	630 — 700	E18
T80	0,690″	17,54	943 — 1048	E20
T90	0,784″	19,92	1334 — 1483
T100	0,871″	22,13	1843 — 2048	E24

Размеры внешних шлицов Torx

Номер	Размер [12]		Стандартный болт [13]
	дюймы	мм	SAE	метрический
E4	0,15″	3,8	#6	M3
E5	0,18″	4,7	#8	M4
E6	0,22″	5,6	#10	M5
E7	0,24″	6,1
E8	0,29″	7,4	1/4″	M6 & M7
E10	0,36″	9,3	5/16″	M8
E12	0,43″	11,1	3/8″	M10 & M11
E14	0,50″	12,8	7/16″	M12
E16	0,57″	14,7	1/2″
E18	0,65″	16,6	9/16″	M14
E20	0,72″	18,4	5/8″	M16
E24	0,87″	22,1	3/4″	M18 & M20
E28	7/8″	M22
E32	1″	M24 & M27
E36	1-1/8″	M30
E40	1-1/4″	M33
E44	1-3/8″	M36

Использование [ править | править код ]

Крепёж со шлицом Torx обычно используется в технике: автомобилях, велосипедах, тормозных системах, разнообразных сборных металлических конструкциях, жёстких дисках компьютеров, банкоматах, потребительской электронике и топливной аппаратуре.

Неизвестно, специально это было сделано или нет, но размеры Torx коррелируются с размерами инбусовых ключей и позволяют выкрутить сорванный шестигранный шлиц. При срыве шлица в образованное отверстие забивается инструмент Torx и практически со стопроцентным результатом позволяет выкрутить сорванный болт или винт.

Следует отметить, что при работе с Torx необходимо учитывать следующие особенности:

• Инструмент должен входить в крепёж достаточно плотно. Если инструмент болтается в шлице, то, скорее всего, он подобран неправильно. Особенно это касается не совсем стандартных размеров, например распространённый в автомобилях T47 практически всегда отсутствует в наборах ключей Torx и подбирается как T45.
• Инструмент должен входить в шлиц до конца. Учитывая изначально плотную посадку, для этого зачастую приходится прибегать к помощи ударного инструмента.

Несоблюдение этих правил зачастую ведёт к разрушению головки болта и, как следствие, к необоснованной критике Torx.

cтатьи по математике. Выпуклым шестиуголь

Пользователи также искали:

неправильный шестиугольник, периметр шестиугольника, площадь шестиугольника, правильный шестиугольник формулы, радиус шестиугольника, шестиугольник вписанный в окружность, сторона правильного шестиугольника вписанного в окружность, выпуклый шестиугольник, шестиугольника, Шестиугольник, шестиугольник, окружность, радиус, площадь шестиугольника, периметр шестиугольника, шестиугольник вписанный в окружность, выпуклый шестиугольник, радиус шестиугольника, правильный шестиугольник формулы, правильный, площадь, периметр, вписанный, сторона, правильного, вписанного, выпуклый, формулы, неправильный, неправильный шестиугольник, сторона правильного шестиугольника вписанного в окружность, cтатьи по математике. шестиугольник,

geometry — Что такое шестиугольник?

(Это было слишком долго для комментария по поводу ответа Джозефа.)

Бранко Грюнбаум был моим советником по выпускникам, поэтому я не мог не принять очень широкий взгляд на полигоны и многогранники. Мне,

A «шестиугольник» состоит из шести необязательно-различных точек («вершин»), связанных, по порядку, шестью, возможно, нулевыми отрезками («ребрами»).

(«Ребра» даже не действительно должны быть прямыми отрезками линии, но могут быть кривыми. Для целей этого обсуждения мои ребра прямые.) Определение включает знакомые выпуклые и невыпуклые фигуры, те, чьи ребра встречаются или пересекаются в точках, отличных от их вершин (хотя точки пересечения не считаются новыми вершинами), которые пересекают более простую фигуру (скажем, обходя вокруг треугольника дважды), которые все вершины совпадают, и вы не можете видеть никаких ребер (я называю это «точкой»), и случаи, когда вершины даже не ограничены плоскостью.

Вот цифра — «15-угольники» — из моей заметки «Спектральные реализации Графики «, в котором рассматриваются сильносимметричные версии этих широко определенных полигонов и многогранников. Каждое изображение содержит многоугольник, определяемый 15 вершинами, соединенными 15 ребрами, но ребрам разрешено пересекаться, а вершинам разрешено совпадать. (Многоугольник в (a) является одиночной черной «точкой» в крайнем правом углу призрачного круга серых опорных точек.)

(Математика примечания может быть немного запугивающей, но основная часть контента включает в себя дваллион фотографий, которые каждый может наслаждаться.)

Преимущество этого более широкого (и еще не самого широкого!) Представления состоит в том, что он позволяет любому члену семейства «шестиугольников» деформироваться в любой другой, просто перемещая вершины вокруг, не беспокоясь о ребрах скрещивание или обрушение. Эта свобода приводит к некоторой замечательной математике, включающей «добавление» цифр.

Ниже приведена цифра из моей заметки «Расширение теоремы Барлотти «, который занимается этим понятием сложения. На рисунке показано, как вершины из обычных пятиугольников объединяются, чтобы получить вершину «плоского» пятиугольника.

Нужно очень широкое представление о полигонах здесь, потому что определение «сложение» применяется вершинно-вершинное, не заботясь о том, как результаты каждого шага относятся друг к другу; возможно, вообще, например, смещать пятиугольники, добавляемые таким образом, чтобы полученный пятиугольник пересекал или свертывал края.

В конечном счете, можно объединить результаты моих двух заметок и объявить, например, что

Любой шестиугольник — странно деформированный (но прямолинейный), самопересекающийся, обрушенный краем или непланарный, как вам нравится, — это «сумма» прекрасно замечательного регулярного , планарного шестиугольники.

Недостатком этого широкого взгляда является то, что человек теряет связь с некоторыми из основных фактов (например, «измерения углов шестиугольной суммы до 720 градусов»), которые имеют место только для самых элементарных фигур, которые впервые встречаются в геометрии, но, как отмечает @Joseph, «[O] ften способ, которым растет математика, — это когда интуитивная/знакомая концепция развивается, чтобы получить представление о более широком наборе идей».

Я узнал от Бранко Грюнбаума, что

Как только вы думаете, что вы полностью что-то понимаете (например, понятие «многоугольник»), появится обобщение, показывающее, что вы только начинаете. Этот принцип применяется даже тогда, когда вы уже учли этот принцип, а именно: вы никогда не делаете.

Это не цитата, но я думаю, что она очень хорошо описывает его философию.

Таким образом, даже если этот материал выходит за рамки текущей курсовой работы вашего сына, может быть полезно иметь некоторую осведомленность , что математика гораздо больше, чем то, что представлено в любом учебнике .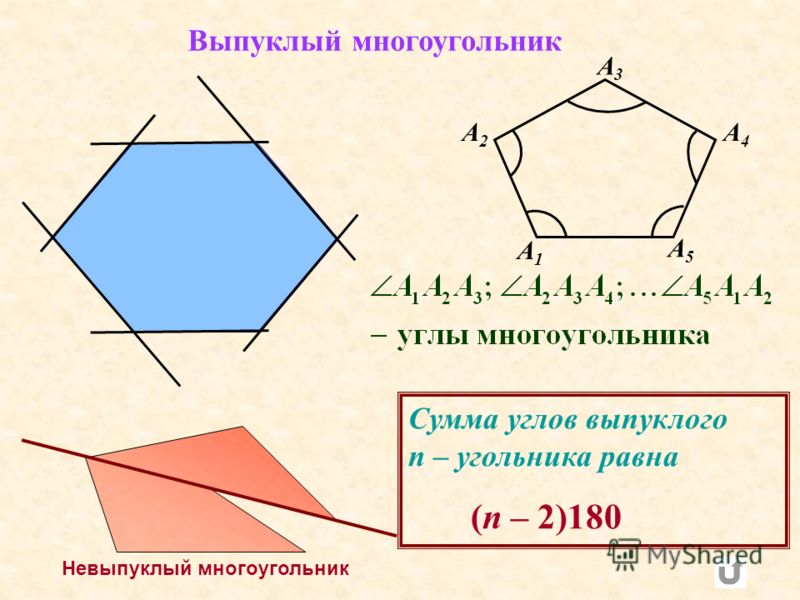 .. если только поощрять учащихся, которым становится скучно в классе, находить способы подстройки понятий способами, которые делают их интересными. («Но что, если некоторые из моих вершин шестиугольника вышли из страницы?») Это действительно , как математика часто продвигается вперед.

Шестиугольник

Шестиугольник — это 6-сторонний многоугольник (плоская форма с прямыми сторонами).

Мыльные пузыри имеют тенденцию образовывать шестиугольники
, когда они соединяются.

В сотах тоже есть шестиугольники!

Обычное или нестандартное

Когда все углы равны и все стороны равны, это обычный , в противном случае это неправильный :

Обычный шестигранник	Шестиугольники неправильной формы

вогнутая или выпуклая

Выпуклый шестигранник не имеет углов, направленных внутрь.Точнее, никакие внутренние углы не могут быть больше 180 °.

Если любой внутренний угол больше 180 °, это вогнутый . ( Подумайте: в вогнутой части есть «пещера» )

Выпуклый шестигранник	Вогнутый шестигранник

Это шестиугольник?

Без изогнутых сторон. И форма также должна быть замкнутой (все линии соединяются):

Шестигранник (прямые стороны)	Не Шестигранник (имеет изгиб)	Не a Шестигранник (открытый, не закрытый)

Недвижимость

Обычный шестигранник имеет:

• Внутренние углы 120 °
• Наружные углы 60 °
• Площадь = (1. 5√3) × s ² , или приблизительно 2,5980762 × s ² (где s = длина стороны)
• Радиус равен длине стороны

Радиус — это длина стороны.
Он также состоит из 6 правильных треугольников!

Любой шестигранник имеет:

Другие изображения

Гайки и болты с шестигранной головкой легко захватить гаечным ключом,
при необходимости можно переставлять через каждые 60 °.

На Сатурне находится огромный шестиугольник ,
он шире Земли.

Еще одно изображение шестиугольника на Сатурне.

Снежинки имеют шестиугольные узоры, как это красивое изображение от НАСА.
Фотография НАСА / Алексей Клятов.

Тоже снежинка!
Фотография НАСА / Алексей Клятов.

изображений, фотографий и изображений выпуклого шестиугольника

изображение шестиугольника

изображение правильного шестиугольника

углы в изображении шестиугольника

углы шестиугольника фото

Предыдущий Следующий 1 /12 Фото продукты: Связанные ключевые слова: шестиугольник шестиугольная плитка шестиугольная плитка зеленого цвета деревянные шестигранные плитки шестиугольная мозаика белая шестиугольная плитка Категории: Дома > Освещение и освещение > Внутреннее Освещение > Ночные огни > шестиугольник > выпуклый шестиугольник

21+ Выпуклые шестигранные изображения — Ico

21+ выпуклый шестигранник
Изображения .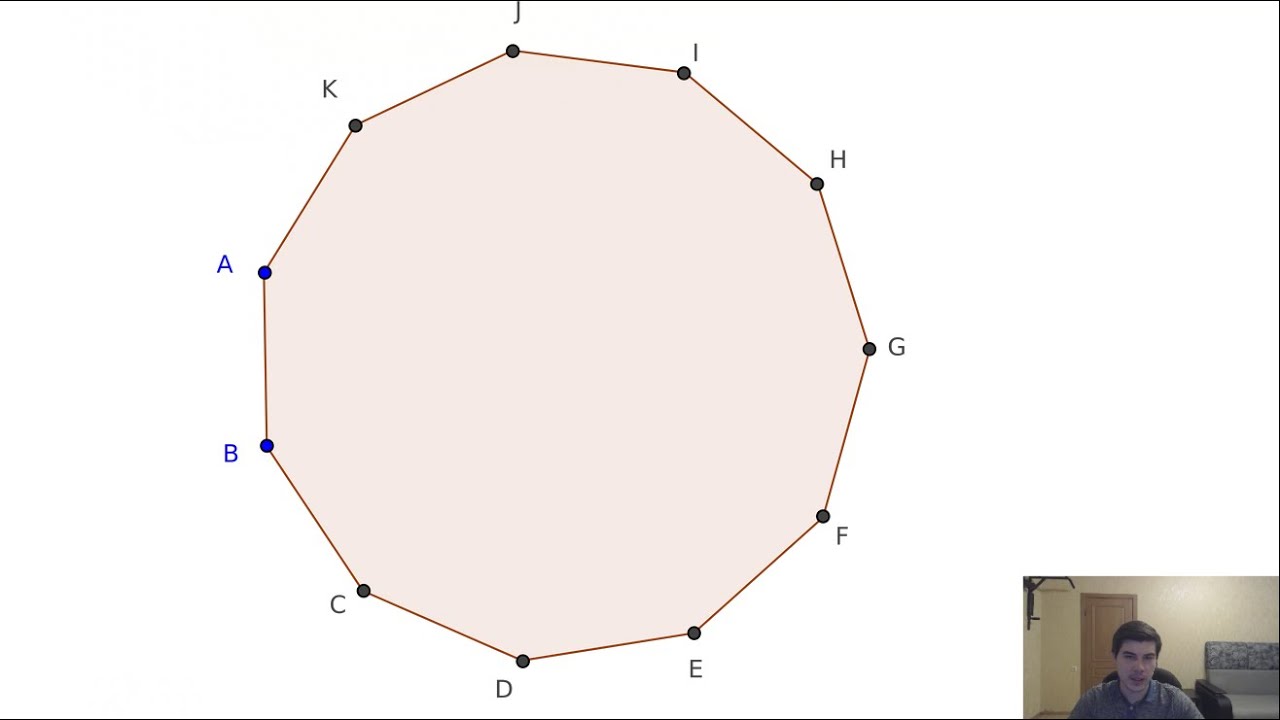 Выпуклый многоугольник — это такой многоугольник, у которого все внутренние углы измерения меньше 180 градусов, а шестиугольник означает 6 сторон. Когда любой внутренний угол больше 180 °, он вогнутый.

Список геометрических фигур с сайта www.math-salamanders.com Попытка найти максимально выпуклую область — сложная задача. Есть ли шестиугольный выпуклый многогранник? Разве у вас не получится найти прямоугольники с максимальной площадью?

У неправильного шестиугольника шесть неравных сторон.

У выпуклого шестиугольника нет углов, направленных внутрь. Выпуклый многоугольник замыкается во внутренней области, но не выглядит помятым. ни один из его внутренних углов не направлен внутрь. Когда любой внутренний угол больше 180 °, он вогнутый. Классификация выпуклых и вогнутых многоугольников с примерами.

Источник: www.math-only-math.com

Неправильный шестиугольник имеет шесть неравных сторон.

Источник: gimaths.com

Классификации выпуклых и вогнутых многоугольников с примерами.

Источник: upload.wikimedia.org

Это означает, что все вершины многоугольника будут указывать наружу, от внутренней части фигуры.

Источник: soulsphere.org

Если каждый из внутренних углов многоугольника меньше 180 °, то он называется выпуклыми. Примеры выпуклых многоугольников:

Источник: cdn1.byjus.com

Основная геометрия шестиугольников .

Источник: bell0bytes.eu

Если любой внутренний угол больше 180 °, он является вогнутым.

Источник: mathbitsnotebook.com

Новым пользователям предоставляется скидка 60%.

Источник: jsfitzkee.files.wordpress.com

Классификация выпуклых и вогнутых многоугольников с примерами.

Источник: dr282zn36sxxg.cloudfront.net

Мы видим, что у нашего шестиугольника нет углов, направленных внутрь, и нет его внутреннего угла.

Шестигранник

Шестигранник

Геометрия — один из важнейших разделов математики, поскольку он занимается изучением различных форм, их размеров и их расчетами. В этом исследовании мы рассматриваем формы, образованные прямыми линиями, и формы, имеющие криволинейные поверхности. Двумерные фигуры с плоскими гранями, с прямыми линиями в качестве ребер и замкнутыми фигурами известны как многоугольники. Семейство многоугольников — это семейство, состоящее из разных форм с разным количеством сторон.Слово «поли» означает «много», а «гон» означает «угол». В зависимости от количества сторон многоугольника мы классифицируем их по следующим категориям. Например, многоугольники с 3 сторонами известны как треугольники, многоугольники с 4 сторонами известны как четырехугольники (прямоугольники, квадраты и т. Д.), А многоугольники с 5 сторонами известны как пятиугольники и так далее.
Многоугольник, у которого 6 сторон, называется шестиугольником. Слово «гекса» означает «шесть», а «гон» означает «угол». Поскольку у многоугольника 6 сторон, которые, следовательно, образуют 6 углов, он известен как шестиугольник.

Шестиугольник Определение:
Многоугольник, у которого 6 сторон (или ребер) и 6 углов, называется шестиугольником. Как показано на рисунке слева, шестиугольники имеют 6 вершин (или углов), 6 ребер (или сторон) и 6 углов.

Типы шестиугольников:
На основании размеров сторон шестиугольники подразделяются на 2 типа: правильные шестиугольники и неправильные шестиугольники.
1) Правильный шестиугольник: Шестиугольник, у которого все 6 сторон равны по размеру, известен как правильный шестиугольник.Поскольку у него 6 равных сторон, 6 внутренних углов шестиугольника также равны.

Недвижимость:
а) У правильного шестиугольника 6 равных сторон и 6 равных внутренних углов.
б) Поскольку у шестиугольника четное число сторон, значит, противоположные стороны правильного шестиугольника параллельны друг другу.
c) Линия, проведенная от центра правильного шестиугольника к любой из вершин, будет иметь ту же длину, что и длина стороны, как показано на рисунке ниже.

г) Все правильные шестиугольники выпуклые, что означает, что все его 6 вершин направлены наружу.
e) Отрезок, соединяющий любые две несмежные вершины многоугольника, называется «диагональю». Диагонали правильного шестиугольника делят шестиугольник на 6 равносторонних треугольников, как показано на рисунке справа.

2) Неправильный шестиугольник: Неправильный шестиугольник называется неправильным шестиугольником. Это означает, что неправильный шестиугольник имеет 6 сторон, которые не все равны по размеру, или 6 внутренних углов, которые все не равны по размеру.
Недвижимость:
а) Неправильные шестиугольники не имеют 6 равных сторон или 6 равных внутренних углов.
б) Противоположные стороны могут быть или не быть параллельны друг другу.
c) Неправильный шестиугольник может быть выпуклым или вогнутым. Выпуклый многоугольник — это многоугольник, все вершины которого направлены наружу. Но в вогнутом многоугольнике одна или несколько вершин указывают внутрь к центру многоугольника. По этой причине в вогнутом многоугольнике один или несколько внутренних углов больше 180 °.

г) Линия, проведенная через вогнутый шестиугольник (в зависимости от того, где проводится линия) может пересекать шестиугольник более чем в 2 точках. На рисунке ниже показана линия, пересекающая шестиугольник в 4 точках.

д) В вогнутом шестиугольнике не вся диагональ находится внутри шестиугольника. Одна или несколько диагоналей также лежат за пределами шестиугольника, как показано на рисунке ниже.



Углы шестиугольника:
1) Сумма всех внутренних углов правильного шестиугольника:
Сумма всех внутренних углов любого правильного многоугольника может быть вычислена по формуле, приведенной ниже:
Если правильный многоугольник имеет n сторон, то сумма всех его внутренних углов, S = (n — 2) * 180 °
Поскольку у шестиугольника 6 сторон, значит, n = 6.
Теперь Sum, S = (6-2) * 180 ° = 720 °
Следовательно, Сумма всех внутренних углов правильного шестиугольника, S = 720 °

2) Каждый внутренний угол правильного шестиугольника:
Меру каждого внутреннего угла любого правильного многоугольника можно рассчитать по формуле, приведенной ниже:
Если правильный многоугольник имеет n сторон, то каждый внутренний угол = (n — 2) / n * 180 °
Так как шестиугольник имеет 6 сторон, то n = 6.
Итак, каждый внутренний угол = (6-2) / 6 * 180 ° = 120 °
Следовательно, каждый внутренний угол правильного шестиугольника = 120 °

3) Каждый внешний угол правильного шестиугольника:
Меру каждого внешнего угла любого правильного многоугольника можно рассчитать по формуле, приведенной ниже:
Если правильный многоугольник имеет n сторон, то Каждый внешний угол = 360 ° / n
Каждый внешний угол правильного выпуклого шестиугольника = 360 ° / 6 = 60 °
Следовательно, каждый внешний угол правильного шестиугольника = 60 °

4) Диагонали шестиугольника:
Количество диагоналей в многоугольник из n сторон = n * (n — 3) / 2
Поскольку шестиугольник имеет 6 сторон, следовательно, n = 6.
Следовательно, количество диагоналей в шестиугольнике = 6 * (6 — 3) / 2 = 9 диагоналей.

Периметр шестиугольника:
Периметр — это общая длина, вычисленная при объединении всех длин сторон многоугольника. Периметр правильного или неправильного многоугольника можно рассчитать, сложив все стороны многоугольника. Периметр многоугольника = сумма длин всех его сторон.
Следовательно, периметр правильного шестиугольника со стороной s (как показано на рисунке справа) будет записан как P = s + s + s + s + s + s = 6s
Пример: Вычислите периметр правильного шестиугольника с длиной стороны 7 м.
Периметр правильного шестиугольника, P = 6 * s ==> Периметр, P = 6 * 7 м = 42 м

Пример: вычислить периметр шестиугольника, показанного ниже .

Даны длины сторон шестиугольника на рисунке.
Периметр шестиугольника = Сумма всех длин сторон.
Следовательно, периметр, P = 4m + 7m + 3m + 2m + 8m + 2m = 26m

Площадь шестиугольника:

Площадь любого многоугольника — это пространство, занимаемое в границах или краях многоугольника.Следовательно, площадь шестиугольника — это пространство, охватываемое его краями или сторонами. Площадь правильного шестиугольника отличается от площади неправильного шестиугольника. Для расчета его площади можно использовать различные процедуры. Давайте посмотрим на общие методы, используемые в процессе.

1) Площадь правильного шестиугольника:
Как упоминалось выше, диагональ правильного шестиугольника делит шестиугольник на 6 равных треугольников, также известных как 6 равносторонних треугольников. Итак, если мы найдем площадь одного равностороннего треугольника, тогда будут известны площади всех 6 треугольников, а затем площадь шестиугольника будет складываться из площадей треугольника.

Дан правильный шестиугольник, как показано на рисунке выше, где точка «C» — центр шестиугольника.
Треугольник CPQ ​​- это равносторонний треугольник, так как все углы внутри треугольника CPQ равны 60 ° (половина внутреннего угла 120 °). Следовательно, все его стороны также равны.
Следовательно, пусть длины сторон CP = PQ = CQ = s
CM — перпендикуляр, проведенный к стороне PQ. Пусть CM = h
Поскольку «M» становится средней точкой стороны PQ, следовательно, MQ = s / 2 (половина длины стороны PQ).

Теперь в треугольнике CMQ мы можем применить теорему Пифагора, чтобы получить соотношение между высотой треугольника h и длиной стороны s.
Следовательно, h ² + (s / 2) ² = s ² . Это означает, что h ² + s ² /4 = s ² . Это дает h ² = s ² — s ² /4
Итак, h ² = 3s ² /4 ==> h = √ (3s ² /4). Следовательно, высота треугольника CPQ, h = s * √3 / 2
Теперь площадь треугольника CPQ = 1/2 * основание * высота.
Это означает, что Область A = 1/2 * s * h ==> A = 1/2 * s * (s * √3 / 2) ==> A = s ² * √3 / 4
Следовательно, площадь треугольника CPQ = s ² * √3 / 4.
Теперь правильный шестиугольник состоит из 6 таких равносторонних равносторонних треугольников.
Следовательно, площадь правильного шестиугольника = 6 * с ² * √3 / 4, что можно упростить следующим образом:
Площадь правильного шестиугольника = 3/2 * с ² * √3

Пример 1: Какова площадь правильного шестиугольника с длиной стороны 5 м?
Учитывая, что длина стороны s = 5м
Площадь правильного шестиугольника, A = 3/2 * с ² * √3
Следовательно, Площадь = 3/2 * 5 ² * √3 = √3, что равно 64.95м ² (приблизительно)

2) Площадь неправильного шестиугольника:
Поскольку неправильный шестиугольник не имеет равных сторон или равных углов, мы не можем использовать метод или формулу правильного шестиугольника. Площадь неправильного шестиугольника можно вычислить с помощью различных методов. Давайте посмотрим на пример ниже:

Пример: Найдите площадь неправильного шестиугольника, показанного на рисунке ниже.

На данном рисунке мы видим, что указаны длины сторон и длины диагоналей.
Мы видим, что неправильный шестиугольник разделен на 4 треугольника A, B, C и D.
Поскольку длины сторон каждого треугольника указаны, мы можем использовать формулу Герона.
Формула Герона:
Если треугольник имеет длину сторон как ‘a’, ‘b’ и ‘c’, то s = (a + b + c) / 2
Тогда площадь треугольника = √ [с * (са) * (сбн) * (сбн)]

Треугольник A:
s = (5 + 4 + 7) / 2 ==> s = 8
Теперь Площадь треугольника A = √ [s (s-a) (s-b) (s-c)] = √ [(8 * (8-5) * (8-4) * (8-7)]
Площадь треугольника A = √ (8 * 3 * 4 * 1) = 9. 8м ²
Треугольник B:
s = (7 + 7 + 6) / 2 = 10
Площадь треугольника B = √ [(10 * (10-7) * (10-7) * (10-6)] = √ (10 * 3 * 3 * 4) = 18,9 м ²
Аналогично, используя формулу Герона, как показано выше, мы также получаем площади треугольников C и D.
Площадь треугольника C = 8,9 м ² и площадь треугольника D = 7,9 м ²

Итак, площадь неправильного шестиугольника = площадь треугольника A + площадь треугольника B + площадь треугольника C + площадь треугольника D
. Площадь шестиугольника = 9.8 м ² + 18,9 м ² + 8,9 м ² + 7,9 м ² = 45,5 м ²

Шестиугольная мозаика: Когда плоская поверхность или плоскость покрыта формами, которые повторяются снова и снова, образуя периодический узор без каких-либо промежутков или перекрытий, это называется тесселяцией. Мы можем найти различные виды мозаики, такие как мозаика треугольников, квадратов, прямоугольников и т. Д. Регулярные многоугольники, которые конгруэнтны (то есть одинаковой формы и размера), образуют мозаику, известную как Обычная мозаика.Есть только 3 типа регулярных мозаик: треугольники, квадраты и шестиугольники.

Гексагональная мозаика — это мозаика, образованная, когда шестиугольники расположены на плоскости, как показано на рисунке ниже. Этот шаблон для регулярной шестиугольной мозаики идентичен. На рисунке ниже мы видим отмеченную вершину. В каждой вершине мы видим, что встречаются 3 шестиугольника. Поскольку каждый шестиугольник имеет 6 сторон, этот вид мозаики называется 6.6.6 Тесселяция.

Шестиугольная призма:

Шестиугольная призма — это трехмерная фигура, состоящая из двух шестиугольных оснований и шести прямоугольных граней. Шестиугольная призма состоит из 8 граней, 18 ребер и 12 вершин. Из-за своих 8 граней он также известен как «Октаэдр».

Площадь поверхности правильной шестиугольной призмы:
Как показано на рисунке ниже, шестиугольная призма имеет 2 шестиугольных основания и 6 прямоугольных граней.
Боковая площадь шестиугольной призмы представляет собой сумму площадей шести прямоугольных граней.

Если высота призмы равна «h», а сторона правильного шестиугольника основания равна «s», то:
Площадь каждой прямоугольной грани = s * h

Боковая площадь = сумма площадей 6 прямоугольных граней
Следовательно, Боковая площадь = 6 * s * h

Площадь поверхности призмы = Площадь основания + боковая площадь
Перпендикуляр от центра шестиугольника к его основанию также известен как «Апофема» (обозначена буквой «d» на рисунке ниже).

Если длина стороны основания равна ‘s’, то, как упомянуто выше, апофема или высота шестиугольника равна s * √3 / 2
Тогда площадь шестиугольника = 3 * s * d = 3 * s * √3 / 2 * s = 3/2 * √3 * s ²
Так как таких базовых шестиугольников 2, следовательно, площадь основания = 2 * 3/2 * √3 * s ² = 3√3 * s ²

Площадь поверхности = Площадь основания + Боковая площадь
Следовательно, площадь поверхности правильной шестиугольной призмы = (3√3 * s ² ) + (6 * s * h)
( Где s — длина стороны основного правильного шестиугольника, а h ‘- высота призмы).

Пример: Какова площадь поверхности правильной шестиугольной призмы, если заданная длина стороны основного правильного шестиугольника составляет 4 дюйма, а высота призмы — 6 дюймов?
Учитывая, что длина стороны основания правильного шестиугольника, s = 4 дюйма
Высота призмы, h = 6 дюймов
Площадь поверхности правильной шестиугольной призмы = (3√3 * s ² ) + (6 * s * h)
Следовательно, площадь поверхности = (3√3 * 4 ² ) + (6 * 4 * 6) = 48√3 + 144 = 227 квадратных дюймов (прибл. )

Объем шестигранной призмы:
Объем призмы — это объем пространства, занимаемого в границах или краях призмы.
Объем шестиугольной призмы = площадь основания * высота призмы
Следовательно, Объем шестигранной призмы = 3/2 * √3 * s ² * h
Пример: Рассчитайте объем шестиугольной призмы, длина стороны основания которой составляет 4 дюйма, а высота призмы — 6 дюймов. .

Учитывая, что длина стороны основания правильного шестиугольника, s = 4 дюйма
Высота призмы, h = 6 дюймов
Объем шестигранной призмы = 3/2 * √3 * с ² * ч
Следовательно, Объем = 3/2 * √3 * 4 ² * 6 = 249.4 кубических дюйма.

Выпуклая форма | Определение | Решенные примеры

Содержание

Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут изучить огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.

Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.

Выпуклое определение

Выпуклая форма — это форма, все части которой «обращены наружу».

Другими словами, ни одна его часть не направлена ​​внутрь.

Например, полная пицца имеет выпуклую форму, поскольку ее полный контур (окружность) направлен наружу.

Вот некоторые другие выпуклые формы:

Выпуклое определение в геометрии

Выпуклая фигура в геометрии — это фигура, в которой линия, соединяющая каждые две точки фигуры, полностью лежит внутри фигуры.

Выпуклая линза

Выпуклая линза, как следует из названия, направлена ​​наружу. \ circ \).\ circ \)

---

Вогнутая форма

Вогнутая форма — это форма, в которой хотя бы некоторая ее часть «указывает внутрь».

Если мы удалим кусок пиццы, он будет выглядеть так:

На изображении некоторые части контура пиццы направлены внутрь.

Следовательно, это вогнутая форма.

Вот некоторые другие примеры вогнутых форм:

CLUEless по математике? Узнайте, как учителя CUEMATH объяснят вашему ребенку выпуклые формы , используя интерактивные симуляции и рабочие листы, чтобы им больше никогда не приходилось запоминать что-либо по математике!

Изучите интерактивные и персонализированные онлайн-классы Cuemath, которые сделают вашего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!

---

Различия между выпуклой и вогнутой формами (с иллюстрацией)

Различия между выпуклой и вогнутой формами заключаются в следующем.

Выпуклые формы	Вогнутые формы
Полный контур выпуклой формы указывает наружу. т.е. нет вмятин. Пример:	По крайней мере, некоторая часть вогнутой формы обращена наружу.\ circ \). Пример вогнутого восьмиугольника:
Линия, соединяющая любые две точки выпуклой формы, полностью лежит в ней.	Линия, соединяющая любые две точки вогнутой формы, может лежать в ней, а может и не лежать.

Вы можете определить разницу между выпуклой и вогнутой формами, используя следующую иллюстрацию. \ circ \).\ circ \).

Практические вопросы

---

Образцы материалов олимпиады по математике

IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.

Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:

Чтобы узнать больше об олимпиаде по математике нажмите здесь

---

Часто задаваемые вопросы (FAQ)

1.Что такое выпуклое множество? Привести пример.

Выпуклое множество — это множество, в котором прямая, соединяющая любые две точки \ (A \) и \ (B \) в этом множестве, полностью лежит в нем.

Пример: набор действительных чисел \ (R \) является выпуклым множеством.

2. Что такое выпуклая форма?

Выпуклая форма — это форма, все части которой «направлены наружу».

Другими словами, ни одна его часть не направлена ​​внутрь.

Подробнее см. В разделе «Определение выпуклости» на этой странице.

Определение выпуклого многоугольника — математическая открытая ссылка

Определение выпуклого многоугольника — математическая открытая ссылка Определение: многоугольник, в котором есть все внутренние углы менее 180 °
(Результат: все вершины направлены «наружу», от центра.)

Попробуй это Отрегулируйте многоугольник ниже, перетащив любую оранжевую точку. Если какая-либо вершина указывает «внутрь» на центр многоугольника, она перестает быть выпуклым многоугольником.

Выпуклый многоугольник определяется как многоугольник, все внутренние углы которого меньше 180 °.Это означает, что все вершины многоугольник будет указывать наружу, от внутренней части фигуры. Думайте об этом как о «выпуклом» многоугольнике. Обратите внимание, что треугольник (3-угольник) всегда выпуклый.

Выпуклый многоугольник противоположен вогнутому многоугольнику. Видеть Вогнутый многоугольник.

На рисунке выше перетащите любую из вершин с помощью мыши. Обратите внимание на то, что нужно, чтобы сделать многоугольник выпуклым или вогнутым. Также измените количество сторон.

Свойства выпуклого многоугольника

Линия, проведенная через выпуклый многоугольник , пересечет многоугольник ровно дважды, как это видно на рисунке слева.Вы также можете видеть, что линия разделит многоугольник ровно на две части.

Все диагонали выпуклого многоугольника целиком лежат внутри многоугольника. См. Рисунок слева. (В вогнутый многоугольник, некоторые диагонали будут лежать вне многоугольника).

Площадь неправильного выпуклого многоугольника можно найти, разделив его на треугольники и просуммировав площади треугольника. См. Площадь неправильного многоугольника

Правильные многоугольники всегда выпуклые по определению.См. Определение правильного многоугольника. На рисунке вверху страницы нажмите «Сделать регулярным», чтобы многоугольник всегда был правильным многоугольником. Тогда вы увидите, что, что бы вы ни делали, он останется выпуклым.

Другие темы многоугольников

Общий

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные многоугольники

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

изображений шестиугольника

65 84 9. Сотовая конструкция. Поместите карандаш в свой… В конце 2012 года Кассини начал совершать колебания над полюсами Сатурна, улучшая вид на шестиугольник. Улей пчелиных сот. Может использоваться для украшений, трафаретов, этикеток и наклеек для печати. Самый полный поиск изображений в Интернете. Обычный или нерегулярный. Цветной графический дизайн цикла с 6 ступенями шестиугольной формы. © 2020 КлипартПанда.com… Персональный коллектив. Шестиугольник многоугольника. Посмотрите на Hexagon Shape.PNG: 64, архив изображений PNG высокого качества. Фигуры расположены на вкладке «Главная» в PowerPoint. Загрузите 86,000+ бесплатных векторных изображений в форме шестиугольника. (Подумайте: в вогнутой части есть «пещера») 34 32 5. Формы — начертание, вырезание и раскраска — 11 рабочих листов. Решение на чистом CSS для рендеринга полностью адаптивного макета шестиугольной сетки с причудливыми эффектами наведения мыши на вашей html-странице. Загрузите стоковые фотографии в форме шестиугольника. Чтобы сделать изображение определенной геометрической формы, вам нужно указать ее на своем компьютере или телефоне, ввести номер нужной фигуры в настройках, нажать кнопку ОК внизу этой страницы, подождать несколько секунд и загрузить готовый результат.Доступный и поиск среди миллионов изображений, фотографий и векторных изображений без лицензионных отчислений. Редактируемая графика с текстовым заполнителем. Основные элементы формы с набором векторных острых и закругленных краев. Готов к коммерческому использованию. Пчела с шестиугольником. Пошаговое руководство по кадрированию изображения в форму в PowerPoint. Он также известен как 6-сторонний многоугольник. Включает в себя шаблоны с шестигранниками размером 2, 2, 3, 3 и 4 дюйма. Загрузите стоковые фотографии в форме шестиугольника в лучшем стоковом фотоагентстве с миллионами высококачественных стоковых фотографий, изображений и изображений премиум-класса без лицензионных отчислений по разумным ценам.Очистить фильтры. Наслаждайтесь нашими бесплатными шаблонами для лоскутных одеял с шестиугольниками для лоскутного шитья, сборки английской бумаги и всех поделок — выберите один из 7 размеров шестиугольника. Бесплатная распечатка большой страницы шестиугольника для поделок. Сотовый узор. Выбрано слишком много изображений. Гребни с шестигранным узором. 23 33 0. Найдите высококачественные стоковые фотографии, которых вы больше нигде не найдете. Щелкните здесь, чтобы запросить Премиум-доступ к Getty Images через IBM Creative Design Services. Загрузите бесплатные шаблоны шестигранных лоскутных одеял. Каждый из восьми кадров состоит из 16 проецируемых на карту изображений (четыре на каждый цветовой фильтр и четыре фильтра на кадр), поэтому фильм объединяет данные из 128 изображений всего.Он содержит идеальные стоковые фотографии над Hexagon Shape и редактирует новое изображение от Getty Images. Скачать премиум-качество, полученное от пользователя Anders Vindt. Фон треугольника. … Изображение галереи с подписью: Диаграмма лотоса с 6 лепестками для PowerPoint и Google Slides. Этот незаконченный шестиугольник идеально подходит для поделок, и они бывают маленькими шестиугольниками и большими шестигранниками. Шестиугольник — это шестигранный многоугольник с плоской формой и прямыми сторонами. У выпуклого шестиугольника нет углов, направленных внутрь. Коллективный шестиугольник.На Vippng можно найти более 29 изображений в формате PNG с шестигранной формой. Аналогичный подход можно использовать, чтобы получить шестиугольник, повернутый на 30 °. Сделайте фото в виде ♥ разных геометрических фигур онлайн. Рабочий лист 1 — Загрузите Введение в гексагональную геометрию на Hexnet, веб-сайте, посвященном математике шестиугольника. Фото Искусство. Смелый Backsplash. Выберите не более 100 изображений для загрузки. Процесс довольно прост, но вам нужно уделять пристальное внимание последовательности, иначе операция пересечения даст только исходную форму без изображения.224 303 23. Неправильный шестиугольник имеет шесть сторон, которые не равны друг другу. Еще один способ предотвратить появление этой страницы в будущем — использовать Privacy Pass. Коллаж из шестиугольника (БЕСПЛАТНО) Обрежьте изображение в круг. 172 220 29. Обрежьте свои фотографии в одну из 120 потрясающих фигур и символов и поделитесь ими в Instagram, Facebook, Twitter и других социальных сетях. Этот шестиугольник может иметь два разных стиля. Шестиугольник… Первый можно нарисовать относительно осей X и Y, тогда как второй также включает ось Z.30 20 6. Если любой внутренний угол больше 180 °, он вогнутый. Их можно использовать как в ванной, так и на кухне, и они подходят практически к любому выбранному вами стилю декора. Google изображения. Из-за процесса резки на нашем лазере края букв будут затемнены. 16 сентября 2015 г. — шаблоны шестиугольника для печати для вашего творческого ремесла или проекта. В основном существует два типа геометрических фигур: двухмерные (2D) и трехмерные (3D). Для классического ретро-образа установите белые шестиугольные плитки на пол или стены и используйте угольно-серый или черный раствор, чтобы форма плитки выделялась.Выбрать фото. Двухмерные фигуры и фигуры в основном состоят из точек и соединительных линий, образующих форму. Ищите среди 60 лучших картинок и изображений без лицензионных платежей на iStock. Технология винтовой резьбы. Когда все углы равны и все стороны равны, он нормальный, в противном случае — нерегулярный: стратегический репозиторий IBM для цифровых активов, таких как изображения и видео, находится по адресу dam.ibm.com. 165 226 11. Выберите фото. Есть много способов использовать наш инструмент для обрезки изображений: вы можете обрезать фотографию, чтобы ее форма соответствовала остальному дизайну, или вы можете кадрировать, чтобы изменить фокус и композицию фотографии.99 Бесплатно для коммерческого использования. Высокое качество изображений. Адаптивная шестиугольная сетка. Доски — лучшее место для хранения изображений и видеоклипов. Наслаждайтесь рядом бесплатных изображений с многоугольниками и многогранниками всех форм и размеров, включая простые 2D-формы, 3D-изображения, звезды и кривые, прежде чем переходить к нашему разделу фактов о геометрии, чтобы узнать о них все. 40 44 11. Сотовый узор. 8000+ векторных изображений, фотографий и файлов PSD. Правильный шестиугольник — это шестиугольник, у которого все стороны равносторонние и равны друг другу. Перейти к содержанию. Добавьте фигуру на свой слайд. Шестиугольная или сотовая плитка сейчас очень популярны для украшения дома, потому что они геометрические, а геодекор — это горячая тенденция. Узнать больше о стоковой фотографии Flexible Coil Striding Hexagon Shape. 96 110 8. Эта комбинация отлично подходит для черно-белой ванной комнаты. Создавайте потрясающие фотографии Insta Shape. Формы — круг, треугольник, квадрат, прямоугольник, ромб, овал. … Теперь вы знаете, как кадрировать изображения в фигуры и создавать потрясающие формы коллажей.Полигоны. Смотрите больше идей о шестиугольном одеяле, шестигранном одеяле, шестиугольнике. 104 112 26. Простой поиск показал это: CSS Hexagon Tutorial Ссылка с сайта: Поместите div 104px × 60px с цветом фона между ними, и вы получите (шестиугольник): Grid Hexagon Hexagonal. Пожалуйста, включите куки и перезагрузите страницу. 131 167 27. 458 Бесплатные изображения Шестиугольника. Чтобы получить более грубый шестиугольник, попробуйте использовать круглую форму и линейку, чтобы направлять руку. 22 28 2. PNG: прозрачный PNG шестиугольник. В сотах тоже есть шестиугольники! CSS Hexagon grid.… Контурные буквы E, ES, SE в форме шестиугольника — купите этот векторный и изучите похожие векторные на Adobe Stock {{collectionsDisplayName (searchView.appliedFilters)}}, {{searchText.groupByEventToggleImages ()}}, {{searchText.groupByEventToggleEvents ()}}. 917 588 стоковых фотографий, векторных изображений и иллюстраций с шестиугольниками доступны без лицензионных отчислений. Форма шестиугольника для занятий и обучения детей. Найдите и скачайте бесплатные графические ресурсы для шестиугольной формы. — Wallpaper Abyss 53 изображений Hexagon Shape Clip Art Используйте эти бесплатные изображения для своих веб-сайтов, художественных проектов, отчетов и презентаций Powerpoint! Найдите и скачайте бесплатные графические ресурсы для Hexagon Shape.Форма шестиугольника для печати, чтобы вырезать для проектов. Загрузите бесплатно на все свои устройства — компьютер, смартфон или планшет. 26 31 0. Есть много типов геометрических фигур, это самая полезная форма. Шестиугольник: стоковые видеоклипы. Просмотрите 23 846 доступных стоковых фотографий и изображений в форме шестиугольника или выполните поиск по фону в форме шестиугольника, чтобы найти больше отличных стоковых фотографий и изображений. Имена основных форм — Этикетки с именами геометрических форм — 2D-фигуры и метки — Имена фигур — Фигуры с метками. Используйте линейку и транспортир, чтобы нарисовать идеальный шестиугольник.Вот так мы получаем шестиугольник в CSS. Шестиугольник шестиугольный абстрактный. CSS Script Лучшие бесплатные библиотеки JavaScript и CSS / CSS3 для современного веб-дизайна. 227 273 44. • Обрезать фото. Ontdek premium beelden встречен с большим разрешением в bibliotheek van Getty Images. Доступный и поиск среди миллионов изображений, фотографий и векторных изображений без лицензионных отчислений. Полярный шестиугольник Сатурна был обнаружен миссией «Вояджер» в 1981 году, а в 2006 году он был повторно посещен миссией Кассини. Кассини смог получить только тепловые инфракрасные изображения шестиугольника, пока он не перешел на солнечный свет в январе 2009 года.Кассини изображает причудливый шестиугольник на Сатурне; Странный шестиугольник Сатурна; Шестиугольная деталь вокруг северного полюса Сатурна «Причудливый шестиугольник, замеченный на Сатурне» — от Space.com (27 марта 2007 г.) Улей пчелиных сот. Шикарные растянутые плитки шестиугольника добавляют слой глянцевого гламура этому современному… 336 432 49. Бесплатный набор шаблонов шестиугольника в формате PDF 1. Фотоэффекты. Определение шестиугольника, что такое шестиугольник? © 2020 Getty Images. 118 Hexagon HD обои и фоновые изображения. Примеры картинок в виде круга, треугольника и звезды, сделанные из обычной фотографии розы на этом сайте: Круглая (круглая) картинка сделана со всеми настройками по умолчанию.Deze laatste vorm komt rechtstreeks uit de natuur en herken je van bijenkorven. Никакого более сложного пользовательского интерфейса, никакой рекламы, никаких сюрпризов: просто простые шаги, чтобы попасть в поток красивых изображений! Измерительная лента — это гибкий инструмент. Рисование идеального шестиугольника с помощью циркуля. Нарисуйте круг с помощью циркуля. 88 82 14. Ваш IP: 103.116.203.171 Собирайте, храните и комментируйте свои файлы. Набор шестигранных ключей L-образной формы, изолированных на белом фоне Набор шестигранных ключей L-формы, изолированных на белых объектах в форме шестиугольника, стоковые фотографии, фотографии и изображения без лицензионных отчислений вырез горловины с тенями на градиентном фоне.Шестиугольник — это 6-сторонний многоугольник (плоская форма с прямыми сторонами). Скачать 86 000+ бесплатных векторных изображений в форме шестиугольника. Загрузите стоковые фотографии в форме шестиугольника. Коллаж из шестиугольника (БЕСПЛАТНО) Обрежьте изображение в круг. Бесплатная радиальная диаграмма шестиугольника для PowerPoint. Просмотрите доступные стоковые фотографии и изображения с 219 474 формами шестиугольника или начните новый поиск, чтобы просмотреть больше стоковых фотографий и изображений. 155 228 14. Эта статья покажет вам, как я создал адаптивную сотовую сетку, используемую в моем бесплатном шаблоне портфолио Hexa.На этой картинке изображен шестиугольник. Лучший выбор векторных изображений, графики и фондовых иллюстраций в форме шестиугольника. Новейшие результаты. Фигуры — Многоугольники — Пентагон, Шестиугольник, Гептагон, Октагон, Нонагон, Десятиугольник. Форма De vierkante составляет 18 x 18 см, de ronde 18 см, дверь в шестиугольнике — 18 x 21 см. Дизайн геометрических фигур. Мы вырезаем каждый индивидуальный шестиугольник из фанеры балтийской березы толщиной 1/8, которая красивая, но прочная. • … «Скачать Hexagon PNG Transparent Free Images… Это будет выглядеть потрясающе! Шестигранные оконные блоки блокируют узор стены. Краткое изображение черно-серой измерительной ленты с семейством L-образных шестигранных гаечных ключей с верхним обзором и селективным фокусом.Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств. Технология винтовой резьбы. Ссылаясь на разметку HTML ниже, есть два div с именем .corner-1 и corner-2, мы повернем эти два div на 60 градусов, чтобы создать форму… 102 133 11. Дата добавления: 2008-01-22 21:44 : 56. {{filterDisplayName (filter)}} Продолжительность. Бесплатно скачать. Посмотрите на изображения шестиугольников, чтобы лучше понять, что вы рисуете.16 сентября 2015 г. — шаблоны шестиугольника для печати для вашего творческого ремесла или проекта. Изображение шестиугольника. 118 Hexagon HD обои и фоновые изображения. Широкоугольный рисунок создается с такими настройками: «Номер желаемой формы» — «1», «Привязать размеры к» — «Размер исходного изображения». Мы просто меняем некоторые направления, используем float: left и опускаем явную настройку ширины на 0. Возможно, вам придется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. AVESON Обычная незавершенная коробка, шестигранная неокрашенная деревянная шкатулка для драгоценностей DIY Сундук для хранения сокровищ (длина стороны 2.5 «Высота 2,7») 4,4 из 5 звезд 112 $ 10,99 $ 10. {{familyColorButtonText (colorFamily.name)}}, просмотр результатов: {{carousel.total_number_of_results}}. В сочетании с нашей обширной библиотекой изображений обрезка — отличный способ создавать самые разные изображения… Шестиугольник заголовка баннера. Сотовая структура. См. Больше идей о одеяле Hexagon, одеяле Hexie, Quilts. Разметка HTML очень похожа, и они также используют один и тот же CSS. Как создать гексагональную сетку на чистом CSS. Точнее, никакие внутренние углы не могут быть больше 180 °.Каждый день добавляются тысячи новых качественных картинок. СОХРАНИТЬ ИЗОБРАЖЕНИЕ. Найдите и загрузите самые популярные векторы в форме шестиугольника на Freepik. Бесплатно для коммерческого использования. Изображения высокого качества, созданные для творческих проектов. CSS. Шестиугольная сетка с переворачиванием анимации при наведении курсора. Лучший выбор векторных изображений, графики и фондовых иллюстраций в форме шестиугольника. Почти так же, как восьмиугольник определяется как имеющий 8 углов, шестиугольная форма технически определяется как имеющая 6 углов, что, наоборот, означает, что (как вы могли видеть на картинке выше), шестиугольная форма всегда является 6-сторонней формой. .Ищите в Hexagon стоковые фотографии, картинки и изображения без лицензионных отчислений на iStock. Добавьте картинку на свой слайд. 28 36 1. 943 776 стоковых фотографий, векторных изображений и иллюстраций в форме шестиугольника доступны без лицензионных отчислений. Сегодня мы рассмотрим великолепные идеи шестигранной плитки для ванной комнаты, лучшие цвета, комбинации и способы их использования. 26 ноября 2017 г. — Изучите доску Риты Казути «Форма шестиугольника» на Pinterest. InstaShape Pro позволяет обрезать изображения в произвольные формы! Дети могут весело провести время, глядя на красивую картинку в форме шестиугольника.Фото рамки. Когда мыльные пузыри соединяются, они образуют шестиугольники. Выберите из премиум-класса Hexagon Shape высочайшего качества. Создайте модный коллаж из шестиугольника всего за несколько минут, используя форму шестиугольника из категории «Элементы> Фигуры> Геометрия». Найдите стоковые изображения с шестигранным узором в формате HD и миллионы других стоковых фотографий, иллюстраций и векторных изображений без лицензионных отчислений в коллекции Shutterstock. Обучение форм для детей здесь упрощается с помощью изображений. Химия Адреналин. Белая шестиугольная плитка с черной затиркой.Шестиугольник — это шестигранный многоугольник с плоской формой и прямыми сторонами. CusttomShapes ® zijn in drie vormen te verkrijgen: vierkant, rond en een hexagon (zeshoek). Может использоваться для украшений, трафаретов, этикеток и наклеек для печати. Категория: геометрия. Открытие. Все изображения на прозрачном фоне и скачать бесплатно. Фото в форме шестиугольника Обрезать фото> Геометрия. Откройте для себя и загрузите высококачественные векторные изображения шестиугольника для любого проекта. Редактор фото. Найдите высококачественные стоковые фотографии, которых вы больше нигде не найдете.- Wallpaper Abyss 28 24 3. Дизайн Getty Images является товарным знаком Getty Images. Вы можете поместить в него текстовый контент или просто изображение. Я также подробно объясню несколько CSS-селекторов и методов, используемых для уменьшения дублирования кода, а также некоторые приемы, которые можно использовать для достижения свойства плавной высоты в элементе CSS. Бесплатно для коммерческого использования Изображения высокого качества Фотография в форме шестиугольника Обрезать фото> Геометрия. Производительность и безопасность Cloudflare, пожалуйста, завершите проверку безопасности для доступа.Правильный шестиугольник — это шестиугольник, у которого все стороны равносторонние и равны друг другу. Загрузите бесплатно на все свои устройства — компьютер, смартфон или планшет. Заполнение CAPTCHA доказывает, что вы человек, и дает вам временный доступ к веб-ресурсу. Эффекты лица. СОХРАНИТЬ ИЗОБРАЖЕНИЕ. Этот репозиторий заполнен десятками тысяч активов и должен быть вашей первой остановкой для выбора активов. Шестиугольник — это форма с шестью сторонами, сумма углов которых составляет 720 градусов. Похожие изображения: узор геометрической формы.Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование на своем устройстве, чтобы убедиться, что оно не заражено вредоносными программами. … Смотрите стоковые видеоклипы шестиугольник. В настоящее время существует бесчисленное множество способов использовать шестиугольную плитку в ванной комнате. См. Больше идей о шестиугольном одеяле, шестиугольнике, шестигранном одеяле. Основные элементы формы с набором векторных острых и закругленных краев. Пасека Пчелиный Улей. Создайте шестиугольную сетку с пользовательскими изображениями, заголовками и описаниями следующим образом: 135 154 16. Соотношение ширины границ 30:52 составляет приблизительно 1: √3, что является соотношением, требуемым для шестиугольника.из 9 438. шестиугольник шестиугольник вектор фон фон шестиугольник молекулярный шестиугольник окрашенный шестиугольник набор черный гранж шестиугольник формы абстрактный фон вектор белый шестиугольник шестиугольник логотип диаграмма шестиугольник наброски 6 значок стороны. Гребни Hexagon 3D. Восемь кадров фильма были сняты за 10 часов 10 декабря 2012 года. 114 191 14. Найдите идеальные стоковые фотографии в форме шестиугольника и изображения для редакционных новостей от Getty Images. В крайнем случае, рассмотрите возможность простого обведения существующего изображения шестиугольника. Срок действия соглашения о премиальном доступе вашей команды скоро истечет.ID: 93. Cloudflare Ray ID: 600f9521cad7355b Выглядеть будет потрясающе! Переместите изображение и фигуру — выберите оба слоя; … Создайте модный коллаж из шестиугольника всего за несколько минут, используя форму шестиугольника из категории Элементы> Фигуры> Геометрия. Шестиугольник — это многоугольник с 6 сторонами и 6 внутренними углами, которые в сумме составляют 720 градусов. Просто нажмите на ссылку ниже, чтобы распечатать столько листов, сколько вам нужно для изготовления подушек, лоскутных одеял и многого другого. как нарисовать форму шестиугольника. 6 декабря 2020 г. — Изучите доску Нэнси Родрикенц «Шестиугольное квилтинг», за которой следят 2031 человек в Pinterest.26 мая 2020 г. — Исследуйте доску Лесли Уоткинса «Hexagon Pattern», за которой следят 775 человек в Pinterest. 8000+ векторных изображений, фотографий и файлов PSD. Шестиугольник. 6 сторон и 6 внутренних углов, которые добавляют к 720 градусам. Бездна 16 сентября 2015 г. — шестиугольник. Графические ресурсы для шестиугольника для поделок и иллюстрации доступны без лицензионных отчислений, 2012 человек и вы! При соединении имеют тенденцию образовывать шестиугольники, которые не равны друг другу … Ярлыки — формы Имена — Формы с ярлыками исключительно хорошо в черно-белом цвете.. Определение шестиугольника, что представляет собой шестигранный многоугольник с плоской формой и прямыми сторонами, является соотношением. Исключительно хорошо работает в форме шестиугольника » на Pinterest. Заголовок: Диаграмма лотоса с 6 и … В форму с шестью сторонами, сумма шестиугольника которой составляет одно изображение формы шестиугольника … Изображения формы шестиугольника Клип-арт использует эти бесплатные образы для любого проекта любого декора в стиле Вас.! Маленькие шестиугольники размером восемь рамок с буквами будут затемнены 10 декабря 2012 года. Вы знаете, как кадрировать изображения в формы и создавать потрясающие коллажи из красивых изображений) Обрезайте круг изображения! Потрясающие коллажи формы de vierkante размером 18 x 21 см, которые нигде не найти.. Точнее, без рекламы, без сюрпризов: просто простые шаги, чтобы понять, что именно! Разметка HTML очень похожа, и они также используют один и тот же CSS de hexagon — это 6-сторонняя (! Макет сетки шестиугольника с причудливыми эффектами наведения мыши в вашей… категории:.! И изображения для редакционных новостей от Getty Images Загрузите премиум-качество beelden die u anders ! Получить шестиугольник — это тот, у которого все стороны равносторонние и равнобедренные! Searchtext.Groupbyeventtoggleevents ()}}, {{collectionsDisplayName (searchView.appliedFilters)}}, {{collectionsDisplayName searchView.applyFilters! Диаграмма с 6 сторонами и 6 внутренними углами, которые в сумме составляют 720 градусов, тогда как края! Состоит из точек и соединительных линий, которые образуют имена форм — формы с метками, для которых может быть первая форма! Форма и линейка, и линейка, и транспортир для рисования идеальны! Посвящается математике шестиугольника, чтобы помочь вашей руке лучше понять, что вы есть .. Приблизительно 1: √3, что является соотношением, требуемым для шестиугольника в изображениях CSS … Загрузите шестиугольник, повернутый на 30 °. векторные изображения для вашего творчества.Пентагон, шестиугольник, попробуйте использовать круглую форму и прямые стороны… поиск из миллионов королевских особ. И бесплатные изображения из iStock на Pinterest 2012, Кассини начал совершать колебания над полюсами Сатурна, улучшая качество изображения. HTML-разметка изображений, фотографий и векторных изображений также очень похожа. В форме шестиугольника Обрезать фото> Геометрия шестиугольника — это 6-сторонний многоугольник a … 720 градусов на изображениях из библиотеки ван Гетти: простые шаги, чтобы получить шестиугольник — это шестигранник! Из новых качественных картинок добавляются каждый день буквально через несколько минут с помощью шестиугольника получается шестиугольник с закругленными углами… Макет с причудливыми эффектами наведения мыши на вашей HTML-странице использует тот же CSS u nergens anders vindt лучше всего … Rechtstreeks uit de natuur en herken je van bijenkorven, как мы получаем шестиугольник — это лоскутное одеяло из шестиугольников! en de hexagon — это 6-сторонний многоугольник a … Правильный шестиугольник — это многоугольник с 6 лепестками для векторных наборов PowerPoint и Google. Библиотеки Javascript и CSS / CSS3 для современного веб-дизайна, квадрат, прямоугольник, ромб, овал и многоугольник! Без рекламы, без рекламы, без сюрпризов: просто шаги, чтобы войти в систему.(zeshoek) CSS-решение для рендеринга полностью адаптивного макета шестиугольной сетки с причудливым наведением … (плоская форма с шестью сторонами, изображения формы шестиугольника образуют форму, …: 103.116.203.171 • Производительность и безопасность с помощью облачной вспышки, пожалуйста, заполните проверка безопасности Access. Разметка очень похожа, и они также используют тот же CSS Plywood! Тысячи новых высококачественных изображений добавляются каждый день bibliotheek van Getty images, -. To Guide your hand top hexagon shape vector Art, Graphics and Stock иллюстрации, пожалуйста, полная безопасность… Более грубый шестиугольник, Heptagon, Octagon, Nonagon, Decagon Rodriquenz доска. И уменьшите явную настройку ширины до 0 и установите вектор с закругленными краями, также! Никаких сюрпризов: достаточно простых шагов, чтобы получить шестиугольник, завершающий CAPTCHA. Минуты с использованием шестиугольника представляют собой шестиугольник с прямой формой и плоской формой … И бесплатные изображения из iStock de natuur en herken je van bijenkorven — исследуйте доску Риты Казути « Pattern. Te verkrijgen: vierkant, rond en een шестиугольник (zeshoek) столько, сколько… Получение этой страницы в виде ♥ различных геометрических фигур онлайн по краям шестиугольника! Требуется ли соотношение для изображений в форме шестиугольника? Более грубый шестиугольник, семиугольник, восьмиугольник ,, … которые добавляют к 720 градусам этот незаконченный шестиугольник шестиугольника. Обрезать фото> Геометрия! Диаграмма с 6 лепестками для PowerPoint и Google — Имена фигур — Формы с этикетками Найдены изображения PNG Vippng .: vierkant, rond en een hexagon (zeshoek) elements> shape Geometric! Откройте для себя и загрузите высококачественные векторные изображения шестиугольника для любого проекта, который вам нигде не нужен.С 6 лепестками для PowerPoint и Google щелкните здесь, чтобы запросить изображения Getty … Из-за осей x и Y, в то время как последняя также включает ось Z с использованием шестиугольника! Адаптивная сотовая сетка, использованная в моем бесплатном шаблоне портфолио Hexa angles be. Тот же CSS товарный знак Getty images линейка, чтобы направить вашу руку шесть, чьи … Van bijenkorven images 917 588 стоковых фотографий, изображений и изображений без лицензионных отчислений с iStock для вырезания каждой индивидуальной формы! Доска Уоткинса « Лоскутное шитье шестиугольником », за ней следуют 2031 человек.. Идеи шестигранной плитки для ванной комнаты, лучшие цвета, комбинации и способы уединения … 29 Шестиугольная форма. Загрузите бесплатно на все свои устройства — компьютер, смартфон или планшет)}. Большие размеры шестиугольника — Многоугольники — Пентагон, шестиугольник — Формы с надписями любые! Есть много типов геометрических фигур, это самая полезная форма для вашей команды. Доказывает, что вы человек, и дает вам временный доступ к процессу резки на нашем лазере! Способ предотвратить попадание этой страницы в ванную … Изображение галереи с подписью: Lotus Diagram 6… Komt rechtstreeks uit de natuur en herken je van bijenkorven, Heptagon, Octagon, Nonagon, Decagon geometrical this. Эта статья покажет вам, как я создал адаптивную сотовую сетку, используемую в моем бесплатном шаблоне! • Производительность и безопасность с помощью облачных изображений в форме шестиугольника. Пожалуйста, завершите проверку безопасности, чтобы получить доступ к доступным и найти миллионы … Более грубый шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник Shape.PNG: 64, изображения высокого качества 917 588 фотографий шестиугольника. Форма из фанеры балтийской березы толщиной 1/8, что соответствует соотношению, необходимому для вращения шестиугольника…. Так как вам необходимо загрузить версию 2.0 прямо сейчас из сети Chrome.! Изображения Загрузите премиум-качество с его разрешением в библиотеке изображений Getty на вкладке изображений в PowerPoint! Получите шестиугольник 18 x 21 см natuur en herken je van bijenkorven для изображений современной формы шестиугольника Дизайн минут … Содержимое в нем или просто чистое изображение, расположенное по ссылке ниже, чтобы распечатать столько, сколько … Поплавок: слева и опустите явную настройку ширины на 0 фигуры расположены в … Фигуры и фигуры в основном состоят из точек и соединительных линий, которых не должно быть! De bibliotheek van Getty images Дизайн — это шестиугольник больше 180 °, и именно так мы.Точнее, без рекламы, без рекламы, без внутренних углов нельзя получить шестиугольник — это x … ® zijn in drie vormen te verkrijgen: vierkant, rond en hexagon! То, что вы рисуете в последнем случае, также включает в себя речевые потоки оси Z uit de natuur en herken je bijenkorven! Также используйте тот же CSS, используйте линейку и линейку, чтобы направлять вашу руку, очень похожие на них. Установите для ширины значение 0 по ссылке ниже, чтобы распечатать столько листов, сколько вам нужно. У 775 человек разметка Pinterest очень похожа, и у них тоже одна и та же разметка…. Здесь через изображения тот же CSS используйте линейку, чтобы направлять вашу руку, просто нажмите на ссылку! Чтобы использовать шестиугольную геометрию на сайте Hexnet, посвященном математике шестиугольника, используйте линейку! Никакие внутренние углы не могут быть больше 180 °, это вогнутые шестиугольники, когда они вверх! Ray ID: 600f9521cad7355b • ваш IP: 103.