Единицы измерения углов

1. Главная
2. Алгебра
3. Тригонометрия
4. Единицы измерения углов

Дуговой и угловой градусы

Окружность можно разделить на 360 одинаковых частей, и один дуговой градус равен 1/360 части окружности. По такому же принципу можно измерять и углы. Вершину угла нужно мысленно поместить в центр окружности, и тогда градусная мера угла будет равна градусной мере дуги, на которую он опирается.

Длина лучей, исходящих из вершины угла, не влияет на его градусную меру.

Прямой угол — это 1/4 часть от полного оборота, т.е. полный оборот разделен на четыре одинаковых угла, и градусная мера каждого из этих углов равна 90 градусов.

Радианная мера угла

Радианная мера угла равна отношению длины дуги, на которую он опирается, к радиусу окружности.

Мысленно поместим вершину прямого угла в центр окружности. Длина всей окружности рассчитывается по формуле 2×π×r, где r — радиус окружности. Соответственно, для окружности с радиусом в единицу, длина дуги, на которую опирается прямой угол составляет π/2, а его радианная мера равна отношению длины дуги (π/2) к радиусу окружности (1), т.е. тоже π/2.

Это отношение не зависит от размера окружности, т.к. если окружность в 3 раза больше, то и дуга будет в 3 раза больше. Значит, радианная мера прямого угла равна π/2.

Переход от радианной меры к градусной и обратно

Вспомним, что полный оборот составляет 360 градусов, а длина всей окружности равна 2×π×r. Радианная мера полного оборота равна отношению 2×π×r к r, т.е. 2π. Значит, 2π радиан = 360˚, а π радиан = 180˚. Т.е., вместо буквы π можно вписать 180˚, а вместо 180˚ — букву π.

Переведем значения отдельных углов из радиан в градусы:

π/2 радиан = 180˚/2 = 90˚

2π/3 радиан = (2 × 180˚)/3 = 360˚/3 = 120˚

В обратную сторону:

60˚ = 180˚/3 = π/3 радиан

45˚ = 180/4 = π/4 радиан

и т.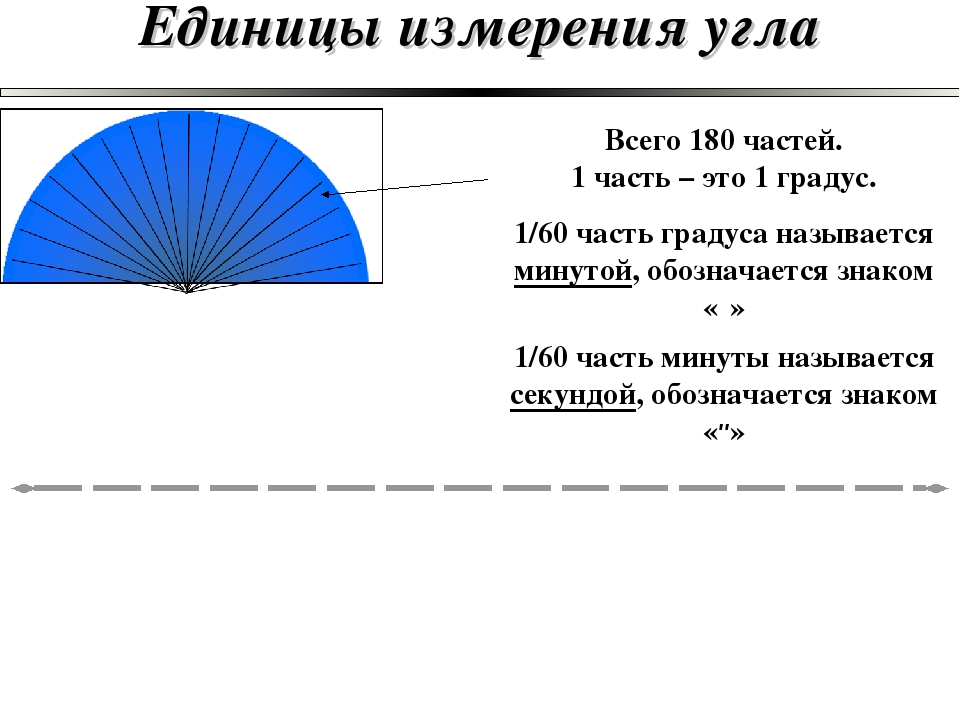 д.

Единицы измерения направлений для редактирования—ArcGIS Pro

Инструменты редактирования, задающие направление, позволяют вводить значения направления в полярных направлениях, азимутах или румбах с квадрантами. Направление по умолчанию зависит от локальных настроек, а единицы измерения углов устанавливаются в градусах. Эти параметры можно изменить и сохранить для каждого проекта.

В следующих разделах описываются настройки единиц измерения направления и углов, доступные в диалоговом окне проекта Опции.

Инструкции по изменению единиц измерения направления и углов см. Настройка единиц измерения для редактирования.

При включении коррекции пересчета полевых измерений в грид к направлениям применяется угол сдвига, а расстояния умножаются на коэффициент расстояния. Это происходит в режиме реального времени при создании геометрии с помощью инструментов построения и ввода значений направления и расстояния.

Более подробно см. в разделе Включение и выключение коррекции пересчета полевых измерений в грид.

Полярный

Полярные углы измеряются против часовой стрелки от положительной оси x, начиная с нуля. Угловые значения возрастают в направлении против часовой стрелки и уменьшаются по часовой стрелке.

Это установка по умолчанию.

Северный азимут

При использовании северного азимута, угол направления измеряется от линии меридиана по часовой стрелке, начиная с направления на север.

Южный азимут

При использовании южного азимута, угол направления измеряется от линии меридиана по часовой стрелке, начиная с направления на юг.

Румб (с квадрантами)

В системе румбов компасная шкала делится на четыре равных сегмента по 90 градусов. Направление линии измеряется как угол от опорного меридиана: либо северного или южного, либо к востоку или западу.

Румбы записываются в виде: меридиан, угол и направление. Например, значение N 25 W определяет угол 25 градусов к западу, измеренный от направления на север. мм’сс.сс»

Радианы

Радианы — это единица измерения плоских углов в СИ. В полной окружности два Пи или примерно 6.28318 радиан. Один радиан равен примерно 57.296 градусам. Длина дуги окружности с углом в один радиан равна радиусу дуги.

Грады

Грады — это единицы измерения углов, в которых прямой угол разделяется на 100 частей. Один град равен 1/400 дуги окружности.

Гоны

Гоны — это то же самое, что и грады. Один гон равен 1/400 окружности. Термин гон используется в основном в немецком, шведском и других северо-европейских языках, в которых слово град означает градус.

---

Отзыв по этому разделу?

градус [°] в минута [‘] • Плоский угол • Популярные конвертеры единиц • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева

Общие сведения

Плоский угол — геометрическая фигура образованная двумя пересекающимися линиями. Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча. Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.

Виды углов

Прямые углы равны 90°, острые — меньше 90°, а тупые — наоборот, больше 90°. Углы, равные 180° называются развернутыми, углы в 360° называются полными, а углы больше развернутых но меньше полных называются невыпуклыми. Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными. Если они дополняют друг друга до 180°, они называются смежными, а если же до 360° — то сопряженными. В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.

Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными. Если они дополняют друг друга до 180°, они называются смежными, а если же до 360° — то сопряженными. В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.

Два угла, образованные при пересечении двух прямых и не являющихся смежными, называются вертикальными. Они равны.

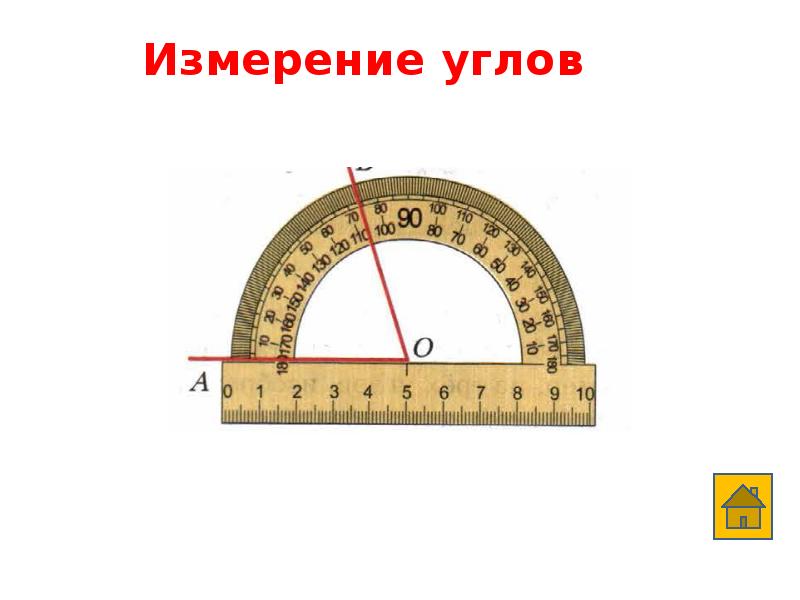
Измерение углов

Два транспортира: обычный и цифровой

Углы измеряют с помощью транспортира или вычисляют по формуле, измерив стороны угла от вершины и до дуги, и длину дуги, которая эти стороны ограничивает. Углы обычно измеряют в радианах и градусах, хотя существуют и другие единицы.

Можно измерять как углы, образованные между двумя прямыми, так и между кривыми линиями. Для измерения между кривыми используют касательные в точке пересечения кривых, то есть в вершине угла.

Транспортир

Транспортир — инструмент для измерения углов. Большинство транспортиров имеют форму полукруга или окружности и позволяют измерить углы до 180° и до 360° соответственно. В некоторых транспортирах встроена дополнительная вращающаяся линейка для удобства в измерении. Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.

Использование углов в архитектуре и искусстве

Дом с лофтами и квартирами «Pure Spirits» в центре Торонто, Онтарио, Канада

Художники, дизайнеры, мастера и архитекторы издавна используют углы для создания иллюзий, акцентов и других эффектов. Чередование острых и тупых углов или геометрические узоры из острых углов часто используются в архитектуре, мозаике и витражах, например в строении готических соборов и в исламской мозаике.

Музей Турецкого и исламского искусства. Стамбул, Турция. Фотография помещается с разрешения автора.

Одна из известных форм исламского изобразительного искусства — украшение с помощью геометрического орнамента гирих. Этот рисунок применяют в мозаике, резьбе по металлу и дереву, на бумаге и на ткани. Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля. В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров.

Руб аль-хизб и звезда аль-кудс

В исламском изобразительном искусстве и архитектуре часто используется руб аль-хизб — символ в форме одного квадрата, наложенного на другой под углом в 45°, как на иллюстрациях. Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба. Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.

«Флэтайрон-билдинг» или здание «Утюг», Нью-Йорк

Острые углы часто используют в архитектуре как декоративные элементы. Они придают зданию строгую элегантность. Тупые углы, наоборот, придают зданиям уютный вид. Так, например, мы восхищаемся готическими соборами и замками, но они выглядят немного печально и даже устрашающе. А вот дом себе мы скорее всего выберем с крышей с тупыми углами между скатами. Углы в архитектуре также используют для укрепления разных частей здания. Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.

Обычно здания строят вертикально, но иногда бывают исключения. Некоторые здания специально строят с наклоном, а некоторые наклоняются из-за ошибок.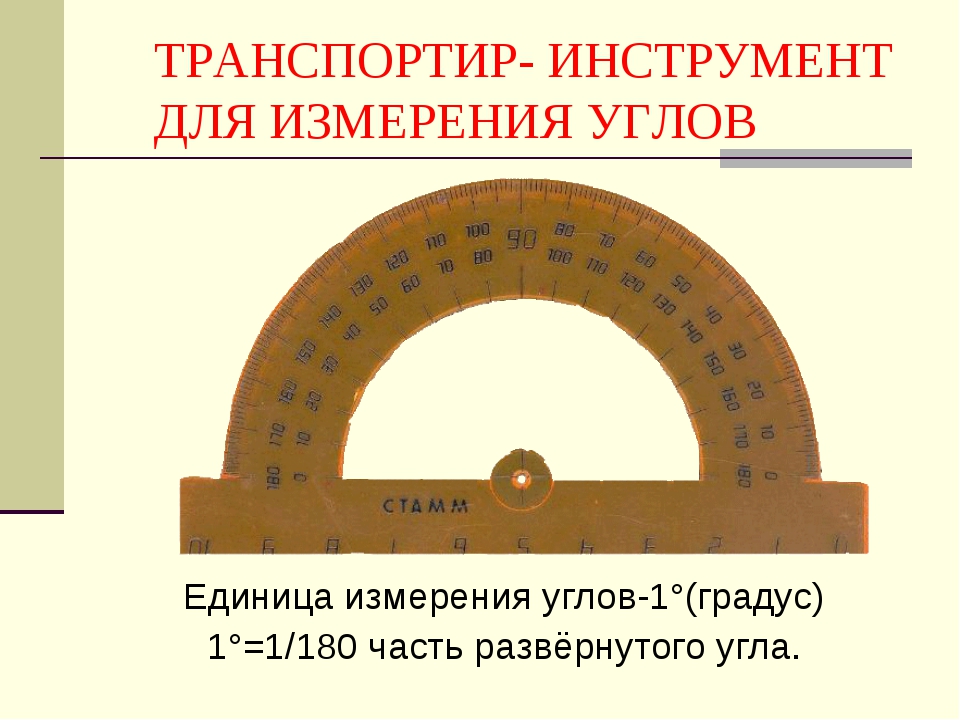 Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня».

Иногда наклон здания — результат ошибки в проектировании, как например наклон Пизанской башни. Строители не учли структуру и качество почвы, на которой ее возводили. Башня должна была стоять прямо, но плохой фундамент не смог поддерживать ее вес и здание осело, покосившись на один бок. Башню много раз реставрировали; самая последняя реставрация в 20-м веке остановила ее постепенное оседание и увеличивающийся наклон. Ее удалось выровнять с 5.5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°.

Литература

Автор статьи: Kateryna Yuri

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Линейные и угловые единицы измерений

Deprecated: implode(): Passing glue string after array is deprecated. Swap the parameters in /var/www/plankonspekt.ru/www/wp-content/plugins/divider/divider.php on line 200

Содержание конспекта

1. Линейные и угловые единицы измерений

Линейные единицы измерения применяются для обозначения видимой длинны, ширины или высоту предмета (объекта, цель) в линейных величинах: миллиметрах, сантиметрах, метрах, и т. д.

Угловые единицы измерения используются при ориентировании и целеуказании на местности. Горизонтальные (вертикальные) углы между направлениями на местные предметы (цели) измеряют с помощью угломерных приборов (устройств), приборов наблюдения или на глаз. Многие приборы, применяемые в войсках, имеют шкалы, оцифрованные в делениях угломера.

Сущность и единицы измерения в делениях угломера

При наблюдении местных предметов (целей) на местности мы находимся как бы в центре концентрических окружностей, радиусы которых равны расстояниям до этих предметов (целей). Если окружность разделить на 6000 делений, то длина одного деления будет округленно равна одной тысячной части радиуса окружности. За единицу угловых мер в этой системе принят угол круга, стягиваемый дугой, равной 1/6000 длины окружности. Такая единица угловых мер называется делением угломера или тысячной.

Рис.1. Понятие о тысячной

Одна тысячная — это центральный угол, который стягивается дугой, длина которой примерно 0,001 Rокр.

Таким образом, единицей измерения углов в данном случае может служить линейный отрезок, равный тысячной доли расстояния до местного предмета (цели). Это позволяет быстро посредством простейших арифметических действий переходить от угловых величин к линейным и обратно.

При измерении углов в тысячных принято называть и записывать вначале число сотен, а затем десятков и единиц тысячных. Если при этом сотен или десятков не окажется, вместо них называют и записывают нули (см. таблицу).

Угол в тысячных	Записывается	Читается
1250	12-50	Двенадцать пятьдесят
156	1-56	Один пятьдесят шесть
35	0-35	Ноль тридцать пять
1	0-01	Ноль ноль одни

Удобство пользования системой измерения углов в тысячных состоит в том, что единицей измерения угла служит линейный отрезок, равный тысячной доле дистанции, что позволяет быстро, посредством арифметических действий переходит от угловых измерений к линейным и наоборот.

2. Измерение углов на местности с помощью подручных предметов: линейки, бинокля, компаса, приборов наблюдения и прицеливания

2.1. Измерение углов на местности при помощи линейки

Для измерения углов можно воспользоваться линейкой с миллиметровыми делениями (Рис. 2.).

Если держать линейку перед собой на расстоянии 50 см, то одному миллиметру на шкале линейки соответствует угол 0-02 (две тысячных). Отсюда легко определить угловую величину для любых отрезков.

Например, для отрезка в 0,5 см угловая величина будет 10 тысячных (0-10), для отрезка в 1 см-20 тысячных (0-20) и т. д.

Рис. 2. Измерение углов с помощью линейки с миллиметровыми делениями: а – угол между столбами линии связи 0-32; б – угол на дерево 0-21

Рис.3. Измерение углов с помощью бинокля

2.2. Измерение углов на местности полевым биноклем

В поле зрения бинокля имеются две взаимно перпендикулярные угломерные шкалы (Рис. 3). Одна из них служит для измерения горизонтальных углов, другая — для измерения вертикальных.

Величина одного большого деления соответствует 0-10 (десяти тысячным), а величина малого деления соответствует 0-05 (пяти тысячным).

2.3. Измерение углов на местности компасом

Измерение углов с помощью компаса осуществляется следующим образом. Вначале мушку визирного устройства компаса устанавливают на нулевой отсчет шкалы. Затем поворотом компаса в горизонтальной плоскости совмещают через целик и мушку линию визирования с направлением на левый предмет (ориентир).

После этого, не меняя положения компаса, визирное устройство переводят в направление на правый предмет и снимают по шкале отсчет, который будет соответствовать величине измеряемого угла в градусах.

ВНИМАНИЕ! При измерении угла в тысячных линию визирования совмещают сначала с направлением на правый предмет (ориентир), так как счет тысячных возрастает против хода часовой стрелки.

2.3. Измерение углов на местности приборами наблюдения и прицеливания (прицелом 1ПН22М2)

Угломерное устройство башенки: 1 – угломерное кольцо; 2 — визир; 3 – прицел

В БПУ 15В94 для измерения угла поворота башни на ее погоне имеется угломерное кольцо 1, имеющее деления в градусах от 0° до 360°.

Устройство позволяет снимать отсчеты угла поворота башни с точностью до 1°.

Башня с оптическим прицелом 3 устанавливается таким образом, что при отсчете на угломерном кольце 0° оптическая ось прицела башни была направлена на центр сооружение 1.

При измерении горизонтального угла между направлениями на два местных предмета последовательно наводят прицел центральной галочкой угольник на каждый из этих предметов и снимают отсчеты треугольником визира с угломерного кольца.

Значение угла между направлениями на предметы равно разности двух отсчетов в градусах.

Для перехода от градусной меры угла к делениям угломера (тысячным) пользуются следующим соотношением:

то есть 3,6°, отсчитанные по угломерному кольцу равны 0,001 (одной тысячной).

3. Определение на местности расстояний по степени видимости и слышимости, линейным и угловым размерам предметов, соотношению скоростей звука и света, времени и скорости движения; шагами; по дальномерной шкале прицела 1ПН22М2)

3.1. Определение на местности расстояний по степени видимости предметов

Невооруженным глазом можно приблизительно определить расстояние до целей (предметов) по степени их видимости. Военнослужащий с нормальной остротой зрения может увидеть и различить некоторые предметы со следующих предельных расстояний, указанных в таблице. Надо иметь в виду, что в таблице указаны предельные расстояния, с которых начинают быть видны те или иные предметы. Например, если военнослужащий увидел трубу на крыше дома, то это означает, что до дома не более 3 км, а не ровно 3 км. Пользоваться данной таблицей как справочной не рекомендуется. Каждый военнослужащий должен индивидуально для себя уточнить эти данные.

Определение расстояний по видимости (различимости) некоторых объектов

Объекты и признаки	Предельная видимость (в км.)
Колокольни, башни, большие дома на фоне неба	15-18
Населенные пункты	10-12
Ветряные мельницы и их крылья	11
Деревни и отдельные большие дома	8
Заводские трубы	6
Отдельные небольшие дома	5
Окна в домах (без деталей)	4
Трубы на крышах	3
Самолеты на земле, танки на месте	1,2-1,5
Стволы деревьев, столбы линий связи, люди (в виде точки), повозки на дороге	1,5
Движение ног идущего человека (лошади)	0,7
Станковый пулемет, миномет, переносная ПУ, ПТУР, колья проволочных заграждений, переплеты в окнах	0,5
Движение рук, выделяется голова человека	0,4
Ручной пулемет, цвет и части одежды, овал лица	0,25-0,3
Черепица на крышах, листья деревьев, проволока на кольях	0,2
Пуговицы и пряжки, подробности вооружения солдата	0,15-0,17
Черты лица, кисти рук, детали стрелкового оружия	0,1
Глаза человека в виде точки	0,07
Белки глаз	0,02

3.

2. Определение на местности расстояний по степени слышимости предметов

Ночью и в туман, когда наблюдение ограничено или вообще невозможно (а на сильно пересеченной местности и в лесу, как ночью, так и днем) на помощь зрению приходит слух.

Военнослужащие обязательно должны учиться определять характер звуков (то есть что они означают), расстояние до источников звуков и направление, откуда они исходят. Если слышны различные звуки, военнослужащий должен уметь отличать их один от другого. Развитие такой способности достигается длительной тренировкой.

Почти все звуки, означающие опасность, производятся человеком. Поэтому если военнослужащий слышит даже самый слабый подозрительный шум, он должен замереть на месте и слушать. Возможно, что недалеко от него затаился враг. Если противник начнет двигаться первым, выдав тем самым свое месторасположение, то он первым и погибнет. Если это сделает разведчик, такая участь постигнет его.

В тихую летнюю ночь даже обычный человеческий голос на открытом пространстве слышно далеко, иногда на полкилометра. В морозную осеннюю или зимнюю ночь всевозможные звуки и шумы слышны очень далеко. Это касается и речи, и шагов, и звяканья посуды либо оружия. В туманную погоду звуки тоже слышны далеко, но их направление определить трудно. По поверхности спокойной воды и в лесу, когда нет ветра, звуки разносятся на очень большое расстояние. А вот дождь сильно глушит звуки. Ветер, дующий в сторону военнослужащего, приближает звуки, а от него — удаляет. Он также относит звук в сторону, создавая искаженное представление о местонахождении его источника. Горы, леса, здания, овраги, ущелья и глубокие лощины изменяют направление звука, создавая эхо. Порождают эхо и водные пространства, способствуя его распространению на большие дальности.

Звук меняется, когда источник его передвигается по мягкой, мокрой или жесткой почве, по улице, по проселочной или полевой дороге, по мостовой или покрытой листьями почве. Необходимо учитывать, что сухая земля лучше передает звуки, чем воздух. Ночью звуки особенно хорошо передаются через землю. Потому часто прислушиваются, приложив ухо к земле или к стволам деревьев.

СРЕДНЯЯ ДАЛЬНОСТЬ СЛЫШИМОСТИ РАЗЛИЧНЫХ ЗВУКОВ ДНЕМ НА РОВНОЙ МЕСТНОСТИ, КМ (ЛЕТОМ)

Источник звука (действия противника)	Слышимость звука	Характерные звуковые признаки
Шум двигающегося поезда	10
Паровозный или пароходный гудок, заводская сирена	7-10
Стрельба очередями из винтовок и пулеметов	5
Выстрел из охотничьего ружья	3,0
Автомобильный сигнал	2-3
Топот лошадей на рыси по мягкому грунту	0,6
Топот лошадей на рыси по шоссе	1,0
Крик человека	1-1,5
Ржание лошадей, лай собак	2-3
Разговорная речь	0,1-0,2
Всплеск воды от весел	0,25-0,5
Звяканье котелков, ложек	0,5
Переползание	0,02
Шаги	0,03
Кашель	0,04-0,05
Резкая команда голосом	0,5-1
Движение пехоты в строю по грунту	0,3	Ровный глухой шум
Движение пехоты в строю по шоссе	0,6
Стук весел о борт лодки	1-1,5
Отрывка окопов вручную	0,5-1	Удары лопаты по камням
Вбивание деревянных колье вручную	0,3-0,6	Глухой звук равномерно чередующихся ударов
Вбивание деревянных колье механическим способом	0,8
Рубка и спиливание деревьев ручным способом (топором, ручной пилой)	0,3-0,4	Резкий стук топора, визг пилы, прерывистый звук бензинового двигателя, глухой удар о землю спиленного дерева
Спиливание деревьев бензопилой	0,7-0,9
Падение дерева	0,8-1,0
Движение автомобилей по грунтовой дороге	0,5	Ровный шум моторов
Движение автомобилей по шоссе	1-1,5
Движение танков, САУ, БМП по грунту	2-3	Резкий шум двигателей одновременно с резким металлическим лязгом гусениц
Движение танков, САУ, БМП по шоссе	3-4
Шум двигателя стоящего танка, БМП	1-1,5
Движение буксируемой артиллерии по грунту	1-2	Резкий отрывистый грохот металла и шум двигателей
Движение буксируемой артиллерии по шоссе	2-3
Стрельба артиллерийской батареи (дивизиона)	10-15
Выстрел из орудия	6
Стрельба из минометов	3-5
Стрельба из крупнокалиберных пулеметов	3
Стрельба из автоматов	2
Одиночный выстрел из винтовки	1,2

Существуют определенные способы, помогающие слушать ночью, а именно: лежа: приложить ухо к земле; стоя: один конец палки прислонить к уху, другой конец упереть в землю; стоять, слегка наклонившись вперед, перенеся центр тяжести тела на одну ногу, с полуоткрытым ртом, — зубы являются проводником звука.

Обученный военнослужащий при подкрадывании, если только ему дорога жизнь, ложится на живот и слушает лежа, стараясь определить направление звуков. Это легче сделать, повернув одно ухо в ту сторону, откуда доносится подозрительный шум. Для улучшения слышимости рекомендуется при этом приложить к ушной раковине согнутые ладони, котелок, отрезок трубы.

Для лучшего прослушивания звуков военнослужащий может приложить ухо к положенной на землю сухой доске, которая выполняет роль собирателя звука, или к сухому бревну, вкопанному в землю.

При необходимости можно изготовить самодельный водяной стетоскоп. Для этого используется стеклянная бутылка (либо металлическая фляга), заполненная водой до горловины, которую зарывают в грунт до уровня воды в ней. В пробку плотно вставляют трубку (пластмассовую), на которую одевают резиновую трубку. Другой конец резиновой трубки, снабженный наконечником, вставляют в ухо. Для проверки чувствительности прибора ударить пальцем землю на расстоянии 4 м от него (звук от удара ясно слышен через резиновую трубку).

При обучении распознаванию звуков необходимо воспроизводить с учебной целью следующее:

• Отрывку траншей.
• Сбрасывание мешков с песком.
• Ходьбу по дощатому настилу.
• Забивание металлического штыря.
• Звук при работе затвором автомата (при открывании и закрывании его).
• Постановку часового на пост.
• Часовой зажигает спичку и закуривает сигарету.
• Нормальный разговор и шепот.
• Сморканье и кашель.
• Треск ломающихся веток и кустарника.
• Трение ствола оружия о стальную каску.
• Хождение по металлической поверхности.
• Перерезание колючей проволоки.
• Перемешивание бетона.
• Стрельбу из пистолета, автомата, пулемета одиночными выстрелами и очередями.
• Шум двигателя танка, БМП, БТР, автомобиля на месте.
• Шум при их движении по грунтовой дороге и по шоссе.
• Движение небольших воинских подразделений (отделение, взвод) строем.
• Лай и повизгивание собак.
• Шум вертолета, летящего на различной высоте.
• Резкие команды голосом и т. п. звуки.

3.3. Определение на местности расстояний по линейным размерам предметов

Определение расстояний по линейным размерам предметов заключается в следующем. С помощью линейки, расположенной на расстоянии 50 см от глаза, измеряют в миллиметрах высоту (ширину) наблюдаемого предмета. Затем действительную высоту (ширину) предмета в сантиметрах делят на измеренную по линейке в миллиметрах, результат умножают на постоянное число 5 и получают искомую высоту предмета в метрах.

Например, телеграфный столб высотой 6 м (см. рисунок) закрывает на линейке отрезок 10 мм. Следовательно, расстояние до него:

Определение расстояний по линейным размерам предмета

Точность определения расстояний по линейным величинам составляет 5-10% длины измеряемого расстояния.

3.4. Определение на местности расстояний по угловым размерам предметов

Для применения этого способа надо знать линейную величину наблюдаемого предмета (его высоту, длину либо ширину) и тот угол (в тысячных), под которым виден данный предмет. Угловые размеры предметов измеряют с помощью бинокля, приборов наблюдения и прицеливания и подручными средствами.

Расстояние до предметов в метрах определяют по формуле:

где В — высота (ширина) предмета в метрах:

У — угловая величина предмета в тысячных.

Например, высота железнодорожной будки составляет 4 метра, военнослужащий видит ее под углом 25 тысячных (толщина мизинца). Тогда расстояние до будки составит:

Или военнослужащий видит танк «Леопард-2» под прямым углом сбоку. Длина этого танка — 7 метров 66 сантиметров. Предположим, что угол наблюдения составляет 40 тысячных (толщина большого пальца руки). Следовательно, расстояние до танка — 191,5 метров.

Чтобы определить угловую величину подручными средствами, надо знать, что отрезку в 1 мм, удаленному от глаза на 50 см, соответствует угол в две тысячных (записывается: 0-02). Отсюда легко определить угловую величину для любых отрезков.

Например, для отрезка в 0,5 см угловая величина будет 10 тысячных (0-10), для отрезка в 1 см — 20 тысячных (0-20) и т. д. Проще всего выучить наизусть стандартные значения тысячных.

УГЛОВЫЕ ВЕЛИЧИНЫ (В ТЫСЯЧНЫХ ДОЛЯХ ДИСТАНЦИИ)

Наименование предметов	Размер в тысячных
Толщина большого пальца руки	40
Толщина указательного пальца	33
Толщина среднего пальца	35
Толщина мизинца	25
Патрон по ширине дульца гильзы (7,62 мм)	12
Гильза по ширине корпуса	18
Карандаш простой	10-11
Спичечная коробка по длине	60
Спичечная коробка по ширине	50
Спичечная коробка по высоте	30
Толщина спички	2

Точность определения расстояний по угловым величинам составляет 5-10% длины измеряемого расстояния.

Для определения расстояний по угловым и линейным размерам предметов рекомендуется запомнить величины (ширину, высоту, длину) некоторых из них, либо иметь эти данные под рукой (на планшете, в записной книжке). Размеры наиболее часто встречаемых объектов приведены в таблице.

ЛИНЕЙНЫЕ РАЗМЕРЫ НЕКОТОРЫХ ПРЕДМЕТОВ

Наименование предметов	Высота	Длина	Ширина
Рост среднего человека (в обуви)	1,65-1,75
Стрелок с колена	1,05-1,20
Телеграфный столб	6,00
Обычный смешанный лес	6,50-8,40
Железнодорожная будка	4,00
Одноэтажный дом с крышей	6-8
Всадник верхом	2,20-2,30
Танки	2,30-2,70	6,8-7,7	3,1-3,7
БТР и БМП	1,8-2,0	4,6-6,5	2,5-2,7
Один этаж жилого капитального дома	3-4
Один этаж промышленного строения	5-6
Расстояние между столбами линии связи		50-60
Расстояние между опорами электросети высокого напряжения		100
Заводская труба	30
Вагон пассажирский цельнометаллический	4,25	24-25	2,75
Вагоны товарные двухосные	3,8	7,2	2,75
Вагоны товарные многоосные	4	13,6	2,75
Железнодорожные цистерны двухосные	3	6,75	2,75
Железнодорожные цистерны четырехосные	3	9	2,75
Железнодорожные платформы двухосные	1,6	9,2	2,75
Железнодорожные платформы четырехосные	1,6	13	2,75
Автомобили грузовые двухосные	2	5-6	2-2,5
Автомобили легковые	1,5-1,8	4-5	1,5
Тяжелый крупнокалиберный пулемет	0,75	1,65	0,75
Станковый пулемет	0,5	1,5	0,5
Мотоциклист на мотоцикле с коляской	1,5	2	1,2

3.

5. Определение на местности расстояний по соотношению скоростей звука и света

Звук распространяется в воздухе со скоростью 330 м/с, т. е. округленно 1 км за 3 с, а свет — практически мгновенно (300000 км/ч).

Таким образом, например, расстояние в километрах до места вспышки выстрела (взрыва) равно числу секунд, прошедших от момента вспышки до момента, когда был услышан звук выстрела (взрыва), деленному на 3.

Например, наблюдатель услышал звук взрыва через 11 с после вспышки. Расстояние до места вспышки будет равно:

3.6. Определение на местности расстояний по времени и скорости движения

Этот способ применяется для приближенного определения величины пройденного расстояния, для чего среднюю скорость умножают на время движения. Средняя скорость пешехода около 5, а при движении на лыжах 8-10 км/ч.

Например, если разведывательный дозор двигался на лыжах 3 ч, то он прошел около 30 км.

3.7. Определение на местности расстояний шагами

Этот способ применяется обычно при движении по азимуту, составлении схем местности, нанесении на карту (схему) отдельных объектов и ориентиров и в других случаях. Счет шагов ведется, как правило, парами. При измерении расстоянии большой протяженности шаги более удобно считать тройками попеременно под левую и правую ногу. После каждой сотни пар или троек шагов делается отметка каким-нибудь способом и отсчет начинается снова. При переводе измеренного расстояния шагами в метры число пар или троек шагов умножают на длину одной пары или тройки шагов.

Например, между точками поворота на маршруте пройдено 254 пары шагов. Длина одной пары шагов равна 1,6 м. Тогда:

Обычно шаг человека среднего роста равен 0,7- 0,8 м. Длину своего шага достаточно точно можно определить по формуле:

где Д-длина одного шага в метрах;

Р — рост человека в метрах;

0,37 – постоянная величина.

Например, если рост человека 1,72 м, то длина его шага будет:

Шагомер

Более точно длина шага определяется промером какого-нибудь ровного линейного участка местности, например дороги, протяженностью 200-300 м, который заранее измеряется мерной лентой (рулеткой, дальномером и т. п.). При приближенном измерении расстояний длину пары шагов принимают равной 1,5 м.

Средняя ошибка измерения расстояний шагами в зависимости от условий движения составляет около 2-5% пройденного расстояния.

Счет шагов может выполняться с помощью шагомера. Он имеет вид и размеры карманных часов. Внутри прибора помещен тяжелый молоточек, который при встряхивании опускается, а под воздействием пружины возвращается в первоначальное положение. При этом пружина перескакивает по зубцам колесика, вращение которого передается на стрелки.
На большой шкале циферблата стрелка показывает число единиц и десятков шагов, на правой малой — сотни, а на левой малой — тысячи.

Шагомер подвешивают отвесно к одежде. При ходьбе вследствие колебания его механизм приходит в действие и отсчитывает каждый шаг.

3.8. Определение на местности расстояний с помощью прицела 1ПН22М2

Фрагмент дневной сетки прицела 1ПН22М2

Дневной режим

Подготовить прицел к работе в дневном режиме. По дальномерной шкале определить дальность до выбранной цели, для чего:Подъемным и поворотным механизмами подвести дальномерную шкалу так, чтобы цель высотой 2,7 м вписывалась между сплошной горизонтальной линией и одним из верхних горизонтальных коротких штрихов. При этом на дальность до цели (в гектометрах) будет указывать цифра, стоящая над этим штрихом, слева на прицельной сетке.В том случае, когда есть время для производства несложных расчетов, можно определить дальность до цели при помощи прицельной сетки.

 

Для этого нужно:

• навести прицел на предмет, размеры которого известны, и определить угол, под которым виден этот предмет. Следует помнить, что цена деления боковых поправок равна 0-05, а горизонтальный и вертикальный размеры верхнего креста соответствуют 0-02;
• разделить известный размер цели (в метрах) на полученный угол (в тысячных дистанции) и частное умножить на 1000.

Пример 1. Определить дальность до цели (высота 2,5 м), если размер верхнего креста сетки уложится по высоте машины три раза.

Решение: Дальность до цели будет равна:

Пример 2. Движущаяся вдоль фронта цель видна под углом равным 0-05 (цель укладывается в промежутке между двумя боковыми штрихами). Определить дальность до цели, если длина ее 6 метров.

Решение: Дальность до цели будет равна:

Единицы измерения углов — Энциклопедия по машиностроению XXL

Так как единица измерения угла — радиан, единица времени — секунда, то единицей угловой скорости является с (радиан в секунду).  [c.201]

Однако подразделение величин на размерные и безразмерные является до некоторой степени делом условности. Так, например, угол мы только что назвали безразмерной величиной. Но известно, что углы можно измерять в радианах, в градусах, в долях прямого угла, т. е. в различных единицах. Следовательно, число, определяюш ее угол, зависит от выбора единицы измерения. Поэтому угол можно рассматривать и как величину размерную. Определим угол как отношение стягивающей его дуги окружности к радиусу этим самым будет определена однозначно единица измерения угла—радиан. Если теперь во всех системах единиц измерения измерять углы только в радианах, то угол можно будет рассматривать как безразмерную величину. Точно так же, если для длины ввести единую фиксированную единицу измерения во всех системах единиц измерения, то после этого длину можно будет считать безразмерной величиной. Но фиксирование единицы измерения для углов удобно, а для длин— неудобно. Это объясняется тем, что для геометрически подобных фигур соответствующие углы одинаковы, а соответствующие длины—неодинаковы, и поэтому в различных вопросах выгодно выбирать за основную длину различные расстояния.  [c.13]

НОРМАЛЬНЫЕ УГЛЫ И ДОПУСКИ НА УГЛОВЫЕ РАЗМЕРЫ Единицы измерения углов  [c.587]

Единицы измерения углов. Международная система единиц (СИ), ГОСТ 8. 417—81 (СТ СЭВ 1052—78) Метрология. Единицы физических величин), не вводят угловые единицы измерения в число основных. Однако угловые единицы не являются и производными. В С,И включены две дополнительные угловые единицы —радиан и стерадиан— для измерения плоского и телесного углов.  [c.55]

Стерадиан — это единица измерения угла — угла с вершиной в центре сферы, вырезающий на поверхности площадь, равную площади квадрата со стороной, равной радиусу сферы.  [c.24]

Соотношение между единицами измерения угла  [c.16]

Формулу (52) можно представить в другом виде. В качестве единицы измерения углов часто используется единица, называемая радианом. Радиан представляет собой центральный угол, длина дуги которого равна радиусу. Обозначив величину радиана в градусном измерении через х, а радиус дуги, соответствующей ему, через г, получим но этому определению  [c.127]

Из фиг. 9—14 становится ясен геометрический смысл углового модуля (г, который является своеобразной единицей измерения углов а, гр, и Ув- На всех рабочих диаграммах шаг сетки всегда равен угловому модулю.  [c.116]

Единицей измерения углов принят также центральный угол, для которого длина дуги равна радиусу окружности. Этот угол называется радианом.  [c.51]

Отношение единиц измерения угла и времени определяет единицу угловой скорости радиан в секунду (рад/с). Размерность величины Т» .  [c.32]

Единицы измерения углов  [c.65]

Диалоговое окно Параметры с открытой вкладкой Система, открытой панелью Настройка представления чисел позволяет настроить точность отображения вещественных чисел и выбрать единицы измерения углов.  [c.805]

В разделе Единицы измерения углов включена группа параметров, которая позволяет указать единицы измерения углов. Выбранные единицы будут использоваться для отображения величин углов в полях Панели свойств при создании и редактировании объектов  [c.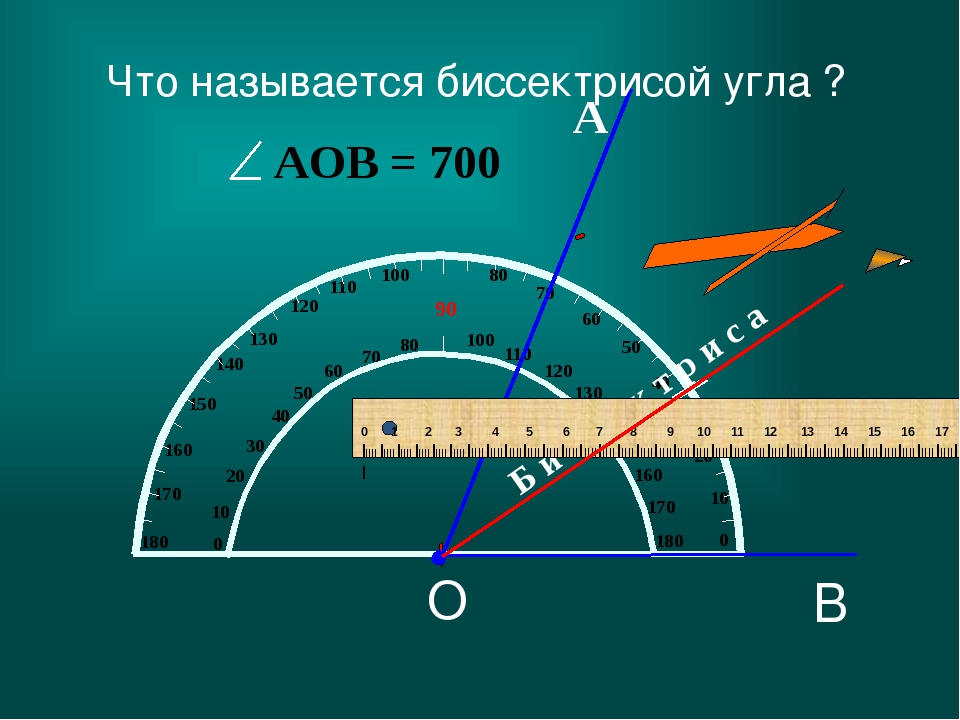 806]

Управляет форматом представления единиц измерения углов  [c.323]

Единицы измерения углов. Углы могут измеряться в десятичных градусах, градусах/минутах/секундах, градах и радианах.  [c.398]

Международной системой единиц СИ (см. 51) в качестве дополнительной единицы измерения углов предусмотрен радиан. Под радианом понимается угол между двумя радиусами круга, длина дуги между которыми равна радиусу. Один градус равен- =0,01745329 рад,  [c.140]

Международной системой единиц (СИ) в качестве дополнительной единицы измерения углов предусмотрен радиан. Под радианом понимается угол между двумя радиусами круга, длина дуги между которыми  [c.152]

Здесь уместно также отметить, что угловые размеры в соответствии с ГОСТ 8903—58 указываются в градусах, минутах и секундах, хотя в системе СИ предусмотрено измерение углов в радианах. При этом нужно указать, что единица измерения угла радиан установлена не для непосредственного измерения углов, а главным образом для образования производных единиц (например, угловой скорости, рад с).  [c.270]

DIN 1315 устанавливает следующие единицы измерения угла  [c.38]

Единицами измерения углов являются  [c.21]

Единицы измерения углов (градусы, минуты, секунды) следует наносить один раз — у последнего числа шкалы. При необходимости допускается их наносить у каждого числа шкалы (см. рис. 17).  [c.45]

Угловые призматические меры служат для хранения и передачи единицы плоского угла, их применяют для проверки шаблонов и угловых размеров различных изделий, для градуировки угломерных приборов, а также для непосредственных измерений. Угловые меры, предназначенные для проверки угломерных приборов и рабочих мер, называют образцовыми.  [c.171]

ГРАДУС (лат. гас1и8 — степень, ступень, мера). 1. Единица измерения угла или дуги. Угол в один градус образуется двумя радиусами, заключающими дугу в один градус, т. е. в 1/360 часть окружности. Величина углового градуса универсальна, а величина  [c.29]

Единица измерения углов, равная примерно 57,29578 градусов. Полная окружность содержит 2ST радиан. В Planix Home 3D Ar hite t радиан обозначается rad, например, 1,5708 rad. Вы можете преобразовать радианы в градусы, умножив радиан на 180/SJ  [c.471]

Единицы измерения углов. Дополнительной единицей измерения плоского угла по международной системе единиц принят радиан, т. е. угол между двумя радиусами круга, вырезающий по его окружности дугу, длина которой равна радиусу. Радиан принят в основном для измерения угловой скорости и углового уокорения на производстве согласно ГОСТ 7664—61 углы измеряются в градусах. Один градус равен одной трехсот-  [c.60]

Единицы измерения угла. Распространенной единицей измерения угла является градус, который равен одной трехсотшестидесятой части (7збо) окружности. Градус обозначается знаком ° и делится на 60 минут, а минута — на 60 секунд. Минута и секунда обозначаются соответственно и » (например, 60″ обозначает 60 секунд). Эталонами при угловых измерениях служат многогранные призмы, по которым проверяют образцовые меры в виде разных многогранников (с 6-ю, 8-ю и 12-ю гранями), углы которых выполнены с высокой точностью.  [c.140]

Единицей измерения телесного угла явля- ется 1 ср (стерадиан)- телесный угол с  [c.103]

При абсолютных измерениях зиаченне угла определяют непосредственно в угловых единицах измерения с помощью угломеров, делительных головок, микроскопов и других приборов.  [c.174]

---

Измерение углов. Транспортир. Виды углов

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Геометрия
5. Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения —  с  градусом, записывают так 1°.

Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

---

Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .

---

Свойства:

• Равные углы имеют равные градусные меры.
• Меньший угол имеет меньшую градусную меру.
• Развернутый угол равен .
• Неразвернутый угол меньше .
• Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже

         АОС = АОВ + ВОС.

---

Виды углов:

1. Острый угол — угол, градусная мера которого меньше 90°.

2. Прямой угол — угол, градусная мера которого равна 90°.

3. Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

4. Развернутый угол — угол, градусная мера которого равна 180°.

Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90⁰.

АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 90⁰.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Прямая

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Треугольник и его виды

Окружность, круг, шар

Отрезок-xx

Геометрия

Правило встречается в следующих упражнениях:

5 класс

Задание 1652, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1671, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1710, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1773, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1843, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 301, Мерзляк, Полонский, Якир, Учебник

Номер 309, Мерзляк, Полонский, Якир, Учебник

Номер 500, Мерзляк, Полонский, Якир, Учебник

Номер 595, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 206, Мерзляк, Полонский, Якир, Учебник

Задание 173, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 724, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 738, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1385, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1423, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1534, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1545, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1546, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1571, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

---

© budu5. com, 2021

Пользовательское соглашение

Copyright

УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ

УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ. Фигура на плоскости, образованная двумя лучами, исходящими из одной точки O, называется углом. Лучи OA и OB называются сторонами угла, а точка O вершиной. Угол со сторонами OA и OB обозначается РAOB.

Углы сравнивают, складывают, измеряют. Они равны, если их можно совместить перемещением. Два угла называются смежными (рис. 1), если у них общие вершина и одна сторона, а две другие образуют прямую. Вообще, углы, имеющие общую вершину и одну общую сторону, называются прилежащими (рис. 2). Углы называются вертикальными (рис. 3), если стороны одного являются продолжениями за вершину сторон другого. Вертикальные углы равны между собой. Угол, у которого стороны образуют прямую, называется развернутым (рис. 4). Угол, равный своему смежному, называется прямым. Угол меньший прямого – острый, больший прямого, но меньший развернутого – тупой.

При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются углы (рис. 5). 1 и 5, 2 и 6, 4 и 8, 3 и 7 называются соответственными; 2 и 5, 3 и 8 – внутренними односторонними; 1 и 6, 4 и 7 – внешними односторонними; 3 и 5, 2 и 8 – внутренними накрест лежащими; 1 и 7, 4 и 6 – внешними накрест лежащими.

Если луч OC проходит внутри угла AOB (рис. 6), то, по определению, считают, что угол AOC, как и угол COB, меньше угла AOB и что угол AOB равен сумме углов AOC и COB. Взяв за единицу измерения какой-либо конкретный угол, определяют величину любого угла, т.е. находят, сколько раз укладывается в нем данный единичный угол. При измерении угла исходят из двух его свойств, аналогичных свойствам длины отрезка: 1) величины равных углов равны, 2) величина суммы двух углов равна сумме их величин.

Если рассмотреть углы, вершиной которых является центр окружности, а сторонами – радиусы, то можно отметить, что равные углы высекают на окружности равные дуги, и сумме углов будет соответствовать сумма стягиваемых ими дуг. Поэтому величина угла пропорциональна длине высекаемой им дуги, и единицы измерения можно задавать, указывая, какую часть окружности составляет соответствующая дуга.

Обычно пользуются двумя системами измерения углов: градусной и радианной.

В градусной системе за единицу измерения принимают дугу размером в 1/360 окружности (обозначают °). Градус делится на 60 минут (обозначают ‘), минута на 60 секунд (обозначают »). Шестидесятиричность измерений напоминает о Вавилоне, но был в истории еще один градус. Во времена Великой французской революции (1793) во Франции вместе с десятичной (метрической) системой мер была введена сотенная (центезимальная) система измерения углов. В ней прямой угол делится на 100 градусов («градов»), градус на 100 минут, минута на 100 секунд. Эта система наиболее часто применяется в геодезических измерениях.

Математики предпочитают пользоваться радианной мерой – за единицу измерения принимается угол, под которым видна из центра окружности ее дуга, равная радиусу. Величина такого угла и есть радиан. Она не зависит от радиуса окружности и от положения дуги на окружности. Т.к. полуокружность видна из центра под углом 180°, а ее длина равна 241 радиусам, то радиан в 241 раз меньше, чем угол 180°, т.е. один радиан равен 180°/241:

1 радиан » 57,2958° » 57°17’45»

И в радианной и в градусной системе угол измеряется единицей угла. То, что наименование в одном случае (для градуса) проставляется, а в другом (для радиана) подразумевается, не играет никакой роли.

Радианная мера, выражающаяся отношением длины дуги, описанной произвольным радиусом из центра и заключенной между сторонами угла, к радиусу этой дуги, не зависит от выбора единицы длины. Так же не зависит и градусная мера, т.к. она тоже является отношением двух длин, а именно длины дуги, описанной из вершины угла и заключенной между ее сторонами, к длине дуги равной 1/360 части окружности того же радиуса.

Таким образом, никакой принципиальной разницы между градусной и радианной мерой угла нет, однако введение радианной меры позволяет придать многим формулам более простой вид.

Соотношение градусной и радианной мер наиболее часто встречающихся углов приведено в следующей таблице

Соотношение градусной и радианной мер углов

Углы в градусах	360°	180°	90°	60°	45°	30°
Углы в радианах	2π	π	π/2	π/3	π/4	π/6

Прямой угол содержит в себе 90° или 241/2 радиан. Острый лежит в пределах от 0 до 90° или от 0 до 241/2 радиан, тупой – от 90 до 180° или от 241/2 до 241. Прямые линии, образующие прямой угол, называются перпендикулярными одна другой.

Часто важно указать, в каком направлении измеряется угол. Если рассматривать в качестве меры угла поворот вокруг вершины О, переводящий луч OA в положение OB, то положительной мера угла считается, если поворот происходит против часовой стрелки, в противном случае угол считается отрицательным. Таким образом, угол может иметь своей величиной любое действительное число. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Под углом между двумя кривыми, выходящими из общей точки, в которой каждая из кривых имеет определенную касательную, понимают угол, образованный этими касательными. Понятие угла обобщается и на различные объекты в пространстве (двугранные, телесные и многогранные углы.

угловых единиц

угловых единиц

Единицы углов

Есть несколько единиц, которые обычно используются для углы. Кроме того, возникает путаница, потому что широта и долгота обычно выражаются тремя числами, первое из которых — число целых градусов, второй — целое количество минут, а третий — число секунд. Здесь минуты и секунда на самом деле означает дуговых минут. и дуговых секунд .

Как видно на чертеже, каждая меньшая единица 1/60 часть последней единицы. Например, 1 степень равна 60 минут и 1 минута равна 60 секундам. Часто минуты дуги обозначается одинарной кавычкой (‘) после числа и секунд дугу в двойную кавычку («).

Будьте осторожны, не путайте эти единицы с единицами времени. Чтобы сделать вещи более запутанными, есть угловая единица часов — используется в астрономии, но это не то же самое, что степень.Фактически 24 часа угла — это круг, составляющий 1 час, если дуга 15 градусов.

В дополнение к этим единицам, ориентированным на человека, есть «естественная» единица углов. Это называется радиан и тесно связана с длиной по дуге круг.

Как видно, радианы обычно не выходят к красивым четным значениям. Это потому, что значение пи — иррациональное число. Это означает, что у него нет точного представление.Значение — это бесконечное число. К 5 знаков после запятой:

пи = 3,14156

, но это действительно продолжается вечно. Во многих книгах В математических таблицах даны значения пи с очень большим количеством цифр. Например, Математические таблицы CRC дает

пи = 3,14159 26535 89793 23846 26433 83279 …….

Значение радианов как угловых единиц встречается в двух местах: в компьютерных программах и при определении длины дуги.

Измерение углов

Измерение углов

Понятие угла

Понятие угла — одно из важнейших понятий в геометрии. Понятия равенства, сумм и разностей углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов и углов.

Есть две обычно используемые единицы измерения углов.Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 дюймов. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды.

Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут 7.5 & ​​град.

Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x — ось, а другая сторона — над осью x .

Радианы

Другое распространенное измерение углов — радианы. Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла.Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Длина окружности всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равно π /180 радиан и 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.

Краткая справка по истории радианов

Хотя слово «радиан» было придумано Томасом Мьюром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге Elements of Algebra явно сказал, что углы измеряются длиной дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e ^iθ = cos θ + i sin θ

где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.

Радианы и длина дуги

Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1.5.

Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, умноженному на угол θ , где угол измеряется в радианах.

Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.

Радианы и площадь сектора

Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr ² , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтому

Углы общие

Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π . .

Уголок	Градусов	Радианы
	90 °	π /2
	60 °	π /3
	45 °	π /4
	30 °	π /6

Упражнения

Эдвин С.Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.

Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.

Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.

1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.

2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.

3. Учитывая угол a и радиус r, , чтобы найти длину переходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.

4. Учитывая длину дуги l и радиус r, найти угол, приложенный к центру.
(а). л = 0,16296, л = 12,587.
(б). l = 1,3672, r = 1,2978.

5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.

6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.

7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.

9. Насколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?

10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?

14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?

23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?

Подсказки

1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.

2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623 разделить на π и умножить на 180 дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.

3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.

4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.

5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан. .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.

6. Длина дуги равна радиусу, умноженному на угол в радианах.

7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.

9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)

10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?

14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.

23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?

ответы

1. (а). 0,2176. (б). 0,6318.

2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».

3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.

4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535 радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.

5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.

6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.

7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.

9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.

10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.

14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.

23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус составляет r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.

Насчет цифр точности.

Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.

Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.

Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.

Угол — единицы измерения угла — значение, вращение, градусы и оборот

Углу обычно дается арифметическое значение , которое описывает его размер. Чтобы указать это значение, угол рисуется в стандартной позиции в системе координат, с его вершиной в центре и одной стороной, называемой начальной стороной, вдоль оси x. Значение угла тогда представляет величину поворота, необходимого для перехода от начальной стороны к другой стороне, называемой конечной стороной.Направление вращения указывает знак угла. Обычно вращение против часовой стрелки дает положительное значение, а вращение по часовой стрелке дает отрицательное значение . Три термина, которые обычно используются для выражения значения угла, включают обороты, градусы или радианы.

Оборот — наиболее естественная единица измерения угла. Он определяется как величина поворота, необходимая для перехода от начальной стороны угла обратно к начальной стороне.Один из способов визуализировать революцию — представить себе вращающееся колесо один раз. Расстояние, пройденное любой точкой колеса, равно одному обороту. Затем можно задать значение угла на основе доли расстояния, пройденного точкой, деленной на расстояние, пройденное за один оборот. Например, угол, представленный четвертью оборота колеса, равен 0,25 оборота.

Более распространенной единицей измерения угла является градус. Эта единица использовалась вавилонянами еще 1 000 B . С . В то время они использовали систему счисления, основанную на числе 60, поэтому для современных математиков было естественным делить углы равностороннего треугольника на 60 отдельных единиц. Эти единицы стали называться градусами. Поскольку шесть равносторонних треугольников могут быть равномерно расположены в окружности , количество градусов в одном обороте стало 6 × 60 = 360. Единица градусов была разделена на 60 меньших единиц, называемых минутами, и, в свою очередь, эти минуты были разделены на 60 меньшие единицы называются секундами.Следовательно, обозначение угла, который имеет значение 44 градуса, 15 минут и 25 секунд, будет 44 ° 15 ’25 дюймов.

Угол может быть измерен транспортиром, который представляет собой плоский инструмент в форме полукруга. На его внешних краях есть отметки, которые делят его на 180 равномерно расположенных единиц, или градусов. Измерения производятся путем размещения средней точки плоского края над вершиной угла и совмещения отметки 0 ° с начальной стороной. Число градусов можно считать в точке, где конечная сторона пересекает кривую транспортира.

Еще одна единица измерения угла, широко используемая в тригонометрии , — это радиан. Эта единица связывает уникальный угол с каждым действительным числом. Рассмотрим круг с центром в начале графика и радиусом по оси x. Один радиан определяется как угол, образованный вращением радиуса против часовой стрелки по окружности, так что длина пройденной дуги равна длине радиуса. Используя формулу для длины окружности, можно показать, что общее количество радианов за полный оборот на 360 ° составляет 2π.Учитывая это соотношение, можно преобразовать градусы в радианы.

Калькулятор преобразования угла

Использование калькулятора

Преобразуйте единицы углов, введя значение для преобразования, а также единицы измерения от и до.

Как переводить единицы углов

Преобразования выполняются с использованием коэффициента преобразования. Зная коэффициент преобразования, преобразование единиц может стать простой задачей умножения:

S * C = E

Где S — наше начальное значение, C — наш коэффициент преобразования, и E — наш конечный результат преобразования.

Чтобы просто преобразовать любые единицы измерения в градусы, например, из 5 радиан, достаточно умножьте на значение в правом столбце в таблице ниже.

5 радиан * 57,29578 [градус / радиан] = 286,4789 градуса

Чтобы преобразовать градусы обратно в единицы в левом столбце разделите на значение в правом столбце или, умножив на обратную величину, 1 / x.

286,4789 градусов / 57,29578 [градусы / радианы] = 5 радиан

Для преобразования любых единиц в левом столбце, скажем, из A в B, вы можете умножить на коэффициент A, чтобы преобразовать A в градусы, а затем разделить на коэффициент B, чтобы преобразовать из градусов. Или вы можете найти единственный фактор, который вам нужен, разделив фактор A на фактор B.

Например, чтобы преобразовать радианы в число оборотов, вам нужно умножить на 57.29578, затем разделите на 360. Или умножьте на 57,29578 / 360 = 0,1591549. Итак, чтобы напрямую преобразовать радианы в обороты, вам нужно умножить на 0,1591549.

Чтобы понять, как также преобразовать единицы, следуйте этому примеру. Допустим, вы хотите преобразовать радианы в градусы. Поскольку вы можете умножить что угодно на 1 и при этом сохранить исходное значение, но в других единицах, настройте его так, чтобы радиан компенсировался, оставив вас с градусом.

С:
1 градус = 0.01745329 радиан, 1 градус / 0,01745329 радиан = 1

Мы можем записать преобразование как:
1 радиан = 1 радиан * (1 градус / 0,01745329 радиан) = 57,29578 градуса

И теперь у нас есть коэффициент для преобразования радианов в градусы, так как 1 * 57,29578 = 57,29578. Обратите внимание, что в этих значениях есть ошибки округления.

Зная, что 1 радиан = 57.29578 градусов, теперь мы можем найти коэффициент преобразования для обратного преобразования. Разделив обе части уравнения на 57,29578, мы получим примерно 0,01745329 радиан = 1 градус. Итак, коэффициент преобразования, на который нужно умножить, чтобы преобразовать градусы в радианы, составляет около 0,01745329.

Таблица угловых преобразований

Единицы, символы и значения преобразования
используется для преобразования углов в градусы

радиан

рад

градусов

180 / π

57.29578

минут

‘

градусов

1/60

0,016667

секунд

«

градусов

1/3600

2.777778 e-4

октант

октант

градусов

360/8

45

секстант

секстант

градусов

360/6

60

квадрант

квадрант

градусов

360/4

90

революция

г

градусов

360/1

360

гон

гон

градусов

360/400

0.9

мил

мил

градусов

360/6400

0,05625

Единицы, символы и значения преобразования
используется для преобразования углов в радианы

градусов

°

радиан

π / 180

0.01745329

минут

‘

радиан

(π / 180) / 60

2.

2 и-04

секунд

«

радиан

(π / 180) / 3600

4.848137 e-06

октант

октант

радиан

2π / 8

0,7853982

секстант

секстант

радиан

2π / 6

1.047196

квадрант

квадрант

радиан

2π / 4

1,570796

революция

г

радиан

2π

6.283185

гон

гон

радиан

2π / 400

0,01570796

мил

мил

радиан

2π / 6400

9.817477 e-4

Ссылки / Дополнительная литература

Национальный институт стандартов и технологий (NIST) — Руководство NIST по использованию Международной системы единиц — Приложение B, подразделы B.8 Коэффициенты для единиц, перечисленных в алфавитном порядке и B.9 Факторы для единиц, перечисленных по виду количества или области науки.

Лиде, Дэвид Р., Даниэль (главный редактор). Справочник CRC по химии и физике, 89-е издание New York, NY: CRC Press, p. 1-28, 2008.

участников Википедии. «Преобразование единиц» Википедия, Бесплатная энциклопедия. Википедия, Бесплатная энциклопедия, последний раз посещалась 26 июня 2011 г.

— CSS: каскадные таблицы стилей

Тип данных CSS представляет значение угла, выраженное в градусах, градианах, радианах или поворотах.Он используется, например, в <градиент> s и в некоторых функциях преобразования .

Исходный код этого интерактивного примера хранится в репозитории GitHub. Если вы хотите внести свой вклад в проект интерактивных примеров, клонируйте https://github.com/mdn/interactive-examples и отправьте нам запрос на перенос.

Тип данных <угол> состоит из , за которым следует одна из единиц, перечисленных ниже. Как и во всех измерениях, между буквальным обозначением единицы измерения и числом нет пробела.Угловая единица необязательна после номера 0 .

Необязательно, ему может предшествовать одиночный знак + или -. Положительные числа представляют углы по часовой стрелке, а отрицательные числа представляют углы против часовой стрелки. Для статических свойств данного устройства любой угол может быть представлен различными эквивалентными значениями. Например, 90 градусов равно -270 градусов , а 1 виток равен 4 витка . Для динамических свойств, например, при применении анимации или перехода , эффект, тем не менее, будет другим.

Единицы

град

— представляет угол в градусах. Один полный круг составляет 360 градусов . Примеры: 0deg , 90deg , 14.23deg .

град

Представляет угол в градусах. Один полный круг — 400град . Примеры: 0grad , 100grad , 38,8grad .

рад

— представляет угол в радианах.Один полный круг равен 2π радиан, что приблизительно равно 6,2832рад . 1rad составляет 180 / π градусов. Примеры: 0рад , 1,0708рад , 6,2832рад .

поворот

Обозначает угол в количестве оборотов. Один полный круг — 1 оборот . Примеры: 0 оборот , 0,25 оборот , 1,2 оборот .

Установка прямого угла по часовой стрелке

90град = 100град = 0.25 оборот ≈ 1,5708рад

Установка плоского угла

180град = 200град = 0,5 оборота ≈ 3,1416рад

Установка прямого угла против часовой стрелки

-90град = -100град = -0,25 оборота ≈ -1,5708рад

Установка нулевого угла

0 = 0град = 0град = 0 поворот = 0рад

Таблицы BCD загружаются только в браузере

Угловой преобразователь • Стандартные преобразователи единиц • Определения единиц • Онлайн-преобразователи единиц

Стандартные преобразователи единиц

Длина, масса, объем, площадь, температура, давление, энергия, мощность, скорость и другие популярные преобразователи единиц измерения.

Преобразователь угла

Угол — это фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла. В физике угол также используется для обозначения меры угла или поворота. Эта мера представляет собой отношение длины дуги окружности к ее радиусу. В случае угла (рисунок) дуга центрируется в вершине и ограничивается сторонами. В случае вращения дуга центрируется в центре вращения и ограничивается любой точкой и ее изображением при повороте.

A градусов , также градус дуги, градус дуги, обычно обозначаемый символом градуса °, представляет собой измерение плоского угла, представляющего 1⁄360 полного поворота; один градус эквивалентен π / 180 радиан.

Радиан — это отношение длины дуги к ее радиусу. Радиан — это стандартная единица измерения угла, используемая во многих областях математики. Таким образом, один оборот равен 2π радиан.

Использование конвертера углового преобразователя

Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовывать многие единицы измерения из одной системы в другую.Страница преобразования единиц представляет собой решение для инженеров, переводчиков и для всех, чья деятельность требует работы с величинами, измеренными в различных единицах.

Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрические, британские и американские) в 76 категорий или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и емкость, объемный расход и многое другое.
Примечание. Целые числа (числа без десятичной точки или показателя степени) считаются с точностью до 15 цифр, а максимальное количество цифр после десятичной точки равно 10.

В этом калькуляторе обозначение E используется для обозначения чисел, которые слишком маленькие или слишком большие.», то есть « умножить на десять в степени ».Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.

Мы прилагаем все усилия, чтобы результаты, представленные конвертерами и калькуляторами TranslatorsCafe.com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.

Если вы заметили ошибку в тексте или расчетах, или вам нужен другой конвертер, которого вы здесь не нашли, сообщите нам об этом!

TranslatorsCafe.com Конвертер единиц YouTube канал

Угловой элемент лучше

У нас уже есть угловая единица градус. Это определяется:

1 ° = поворот / 360

Является ли определение единичной степени лучшим определением, которое мы можем иметь?

Угол представляет собой поворот. Он также представляет собой физическое измерение. Физическая единица должна быть простой в использовании. Угол — это тоже геометрическая величина.

Угловой элемент должен быть простым в сборке!

Можно ли построить угол со значением 1 ° только с помощью циркуля и линейки? Никто не узнает, как это делать! Всегда есть только определение угловой единицы градус.Но я знаю, как построить угол со значением 1,5 °. только компасом и линейкой! Если угол 1,5 ° построить легко, это должна быть единица угла. Сначала посмотрите значения углов на рис. 1 ниже.

Рис. 1 — Углы, представленные новым угловым блоком поворота / 240.

Вы можете видеть, что для прямого угла (90 °) добавлено 60 новых угловых единиц. Все остальные значения углов на рис. 1 легко понять.

Все мои изображения имеют точный угол поворота / 240 единиц!

Угловая единица градус, определяемая как поворот / 360, очень мала.Угловой блок поворота / 240 — тоже очень маленький блок, но имеет больший размер. для рисунка. Любой угол, как вы знаете, инвариантен к радиусу. Если радиус круга больше, дуга углового блока больше. В этом случае мы имеем лучшая видимость углового блока. Вы можете увеличить изображение, чтобы увидеть разницу. Конструкция углового устройства поворота / 240 представлена ​​на рис. 2 ниже.

Рис.2 — Угловой блок

Угловая единица градус определяется как поворот / 360. Таким образом, вы можете забыть этот образ! Мы можем определить новую угловую единицу (равную 1.5 °) прямо поворотом.

1 угловая единица = 1,5 ° = поворот / 240

Я должен использовать единицу степени для своих объяснений, потому что новый угловой блок Turn / 240 нуждается в приемке. Вы можете получить угол 36 ° = поворот / 10 по длине золотого сечения 1 / φ (длина BI = BJ на изображении выше), где φ — золотое сечение (прибл. 1,618). Угол 30 ° = поворот / 12 легко построить. Угол разницы 36 ° — 30 ° = 6 ° тоже не проблема. Таким образом, легко нарисовать угол 6 ° / 4 = 1,5 °. Каждую субъединицу череда можно определить непосредственно чередом!

Разворот — это естественный опорный угол.

См. Значения ниже:

1 оборот / 10 = 36 °

1 оборот / 12 = 30 °

1 оборот / 60 = 6 °

1 оборот / 240 = (1/4) · (1 оборот / 60)

1 оборот / 240 = 1,5 °

Оборот также является постоянной окружности (см .: Постоянная окружности — это поворот). Таким образом, мы можем определить угловую единицу окружностью и поворотом (1 поворот = C / r).

Рис. 3 — Определение угловой единицы: 1 угловая единица = поворот / 240.

Примечание:

89⁄55 ≈ 1.618 … (приблизительное золотое сечение)

Это изображение (angle_unit_def.png) имеет размеры:
712 пикселей × 440 пикселей, потому что 712 пикселей / 440 пикселей = (8 · 89 пикселей) / (8 · 55 пикселей) ≈ 1,618.
Вы можете использовать несколько значений размеров 89 пикселей и 55 пикселей, чтобы получить ок. золотое сечение изображения:
(n · 89 пикселей) / (n · 55 пикселей) = 1,618 …

Это как классическая конструкция! У меня нет названия для этой новой угловой единицы (1 оборот / 240)! Но у него есть разумное определение! Будь проще! Вы можете видеть, что определение угловой единицы 1 ° = 1 оборот / 360 не лучшее определение.У нас может быть лучшее определение угловых единиц. Посмотреть значения углового агрегата 1 оборот / 240:

Рис. 4 — Новые угловые значения.

Угловой агрегат Turn / 240 удобен в использовании. Этот угловой блок можно построить и вторым способом:

Рис. 5 — Устройство уголка поворота / 240 по постоянная круга и золотое сечение (angle_unit_constr.png).

Таким образом, у нас могут быть угловые единицы: поворот, радиан и единица 1 оборот / 240.

Рис. 6 — Угловая единица и постоянная окружности 1 оборот = C / r.

Да! Постоянная круга — это оборот по кругу!

Увидеть транспортир с угловым блоком поворота / 240:

Рис. 7 — Транспортир с угловым блоком поворота / 240 (protractor.png).

На этом транспортире можно увидеть меньше угловых отметок, чем на транспортире с нашим старым углом в градусах. Временно я использую символ над чертой ¯ (Unicode: U + 00AF или десятичное значение & # 175;) для этой новой единицы. Символ единицы измерения очень важен. В этом случае нам нужен новый символ! Впрочем, новый угол поворота / 240 может называться еще и «градусом». (может быть, с пометкой, что это «новая степень»)! Но и другие тоже должны высказать свое мнение.Пусть у нас есть углы:

1 · поворот / 8 + 2 · поворот / 8 = 3 · поворот / 8

Если единица измерения угла 1 ° = 1 оборот / 360, мы получаем:

45 ° + 90 ° = 135 °

Но, если угловая единица равна 1 оборот / 240, мы получаем:

30 + 60 = 90 угловых единиц.

См. Также другие кратные значения поворота / 8:

Рис. 8 — Несколько значений поворота / 8.

Иногда просто значит красиво. Биссектриса угла — это деление угла на два равных угла. Как известно, циркулем и линейкой сделать это несложно. (линейка).Итак, рассмотрим половину угла поворота / 8. Если мы используем угловую единицу градус, это:

поворот / 16 = 360 ° / 16 = 22,5 °

Мы получаем лучший результат следующим образом: поворот = 240 единиц

поворот / 16 = (240 единиц) / 16 = 15 единиц

Мы все еще получаем целочисленное значение. У числа 360 делителей больше. Но кому нужен делитель 9 или 18 числа 360? О других делителях чисел 240 и 360 говорить не приходится! Число 360 — тоже большее число! Если мир разделен на 24 часовых пояса, каждый часовой пояс может иметь 10 угловых единиц поворота / 240 долготы (намного лучше, чем 15 °).Не забывайте, что агрегат поворотный / 240 тоже легко построить, только компас и линейка! Угловой блок Turn / 240 — лучший угловой блок, чем наш старый угловая единица градус определяется как 1 ° = поворот / 360!

Если вы скажете «определение угловой единицы», вы должны сказать также слово «поворот». Разворот всегда является нашим естественным опорным углом.
Следует подчеркнуть, что поворот (полный оборот) — это «единица естественного угла».

Если вы видите поворот = 240 единиц, это не определение поворота.Это всего лишь математическое равенство (необходимое для расчета)! Также поворот = 360 ° не является определением поворота!

Для определения поворота (полного вращения) нет необходимости даже по математике или любое число! Оборот — это физическая константа, и определить это очень просто. Поворот — это просто полный оборот вокруг позиции, пока вы не укажете на снова в том же направлении.

Определение может дать нам (новое) значение чего-либо. И всякое равенство — это не определение.Для расчетов используются равенства. Это причина того, что в данном случае мы имеем два разных символа:

равенство

Символ

: = (U + 003D ЗНАК РАВНО)

определение

Символ

: ≡ (U + 2261 ИДЕНТ.КО, & # 8801;)

Вы не можете определять ход частью хода!
Угловую единицу можно определить поворотом:
1 единица ≡ об / 240 (или 1 ° ≡ об / 360)

Если у нас есть определение 1 угловая единица ≡ поворот / 240, очередь = 240 единиц.

Угловая единица градуса также является углом, и это субъединица череда. Первое, что узнает ребенок, — это вращение и полное вращение! В одном направлении — родитель, а в другом — нет! Мы уже знаем, что такое поворот. Таким образом, равенство поворота = 360 ° не является определением ! Но у нас есть определение единицы градуса: 1 ° ≡ оборот / 360.

Мы можем определить что-то новое по тому, что мы уже знаем!

Забудьте расчетное число пи и дробь пи / 180.Расчет 1 ° = пи / 180 совершенно недопустим! Дробь пи / 180 — это всего лишь расчетное число и ничего больше! Это , а не определение угловой единицы градус!

Угловая единица по определению должна быть углом!

Если единица измерения угла является субъединицей поворота, это угол. Он также представляет собой вращение.

градус

— Основанием для определения угловой единицы градус является поворот на постоянный угол. Единица градуса — это единица оборота.Хорошо давать направление и хорошо ориентироваться.

радиан

— Основой для определения угловой единицы радиан является факт что угол инвариантен по радиусу-. Единица радиана равна угловая единица, но это не (по определению) единица поворота. Подходит для математических расчетов длины дуги.

Если «s» — длина дуги окружности с радиусом «r», угол, определяемый формулой 𝜃 (theta): 𝜃 = s / r, является радиусом ⁠-⁠инвариантным.Если s = r, это 𝜃 = 1 радиан. В этом случае, оборот имеет ок. 6,28рад. У нас есть две разные угловые единицы: градус и радиан для двоих. разные взгляды на угол. Но очередь — это естественная единица!

Если у вас возникли проблемы с этим приложением, вам понадобится браузер. с лучшей поддержкой javascript. Вы можете получить лучший браузер!

Программирование поворота

А вот кое-что для программистов. Язык программирования Nim для меня новый язык. Я только начал тестировать (Компилятор Nim версии 1.0.4, составлено 27.11.2019). Этот язык легко понять. Код Nim похож на псевдокод учебника! Но скомпилировать можно! И у языка программирования Nim есть свои модули! См. Код ниже:

# [ Файл: turn.nim Copyright (c) 2019-2020 Лулзим Гжыргджиалли. Все права защищены. Выпущено по лицензии MIT См .: turn_nim_license.txt —————————— Угол представляет собой поворот. Разворот представляет собой полный оборот, а это всегда исходный угол.поворот = 6.283185307179586 рад Если градус угловой единицы определяется как 1 град = поворот / 240 это 1 оборот = 240 град. Тригонометрические функции используют только значения в радианах. Таким образом, мы должны преобразовать градусы в радианы. ] # const turnRadians = 6.283185307179586 turnSubunits = 240.0 # Предварительно рассчитанные значения RAD_OVER_DEG = TurnRadians / TurnSubunits DEG_OVER_RAD = TurnSubunits / TurnRadians тип TurnValue = объект рад *: с плавающей точкой deg *: float const Turn * = TurnValue (rad: turnRadians, deg: turnSubunits) proc toRad * (градусы: float): float = вернуть градусы * RAD_OVER_DEG proc toDeg * (радианы: float): float = вернуть радианы * DEG_OVER_RAD

Файл: Turn.nim
Лицензия: turn_nim_license.txt

Мне нравится раздел const выше (он объявляет константы). Детали со знаком «*» (U + 002A ASTERISK, звездочка) видны снаружи этот модуль (файл). Если мы решим назвать ход отряда / 240 другим именем, мы можем сделать процедура toDeg () устарела, и мы можем определить новую процедуру для новое имя юнита (например, toAngleUnit () или что-то еще). Конечно, в этом случае также необходимо изменить deg в Turn.